Efekty relatywistyczne bez teorii względności

Zasada względności została po raz pierwszy jasno wyrażona w słynnym dziele Galileusza Dialog o dwóch najważniejszych układach świata w 1632 roku. Dzisiaj często formułuje się ją w następujący sposób: prawa fizyki są takie same we wszystkich inercjalnych układach odniesienia. Wystarczy znaleźć jeden układ inercjalny - pozostałe poruszają się względem niego ruchem jednostajnym prostoliniowym. Zasada względności niejednokrotnie okazywała swą zadziwiająco dużą moc poznawczą...
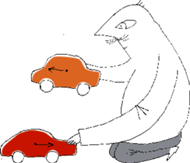
Zaledwie 20 lat po jej sformułowaniu Christiaan Huygens zastosował ją do opisu zderzeń całkowicie sprężystych. Zrozumiał on, że wystarczy założyć jeden "oczywisty" wynikający z symetrii przypadek: dwie identyczne kule zderzające się z tymi samymi prędkościami mają po zderzeniu prędkości przeciwne. Potem zastosował zasadę względności. Wyobraźmy sobie, że opisane zderzenie przeprowadzamy na łodzi poruszającej się względem lądu (rycina obok). Aby otrzymać prędkości kul względem lądu, trzeba do ich prędkości względem łódki dodać prędkość samej łódki. W ten sposób, stosując zasadę względności, łatwo uzyskamy wzory na prędkości kul po zderzeniu dla ich dowolnych prędkości przed zderzeniem.
Przy zastosowaniu podobnych metod opisano dokładnie zderzenia sprężyste i niesprężyste jeszcze przed sformułowaniem przez Newtona zasad dynamiki.

Rys. 1. Dwa równoległe identyczne szeregi ładunków dodatnich
Bardzo wdzięcznym obiektem rozważań z użyciem zasady względności Galileusza jest tzw. siła elektrodynamiczna, czyli siła, z jaką działają na siebie (poprzez pole magnetyczne) dwa przewodniki z prądem. Będziemy ją nazywać siłą magnetyczną. Rozważmy szczególnie prosty przypadek przedstawiony na rysunku 1.

Rys. 2. Ładunki z rysunku 1 obserwowane z układu poruszającego się z prędkością  w lewo
w lewo
Rozpatrujemy dwa równoległe identyczne sztywne szeregi spoczywających ładunków dodatnich, np. protonów. Nie będziemy się interesować siłami utrzymującymi ten układ w równowadze. Na rysunku 1 zaznaczono siłę elektryczną, jaką górny szereg działa na jednostkę długości szeregu dolnego. Teraz przejdźmy do układu poruszającego się względem tego "spoczywającego" z prędkością  w lewo (Rys. 2).
w lewo (Rys. 2).
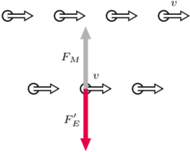
Rys. 3. Siły elektryczna i magnetyczna działające na dolny prąd
Nasze szeregi są w tym układzie prądami elektrycznymi. Górny prąd wytwarza pole magnetyczne, które działa na jednostkę długości drugiego prądu siłą elektrodynamiczną (Rys. 3) o wartości
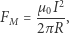 |
(1) |
gdzie 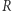 to odległość między szeregami ładunków, a
to odległość między szeregami ładunków, a 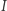 to natężenie prądu takie samo dla obu szeregów wynoszące
to natężenie prądu takie samo dla obu szeregów wynoszące
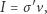 |
(2) |
gdzie 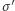 jest gęstością liniową ładunku. Na dolny szereg działa też przeciwnie skierowana siła elektryczna o wartości
jest gęstością liniową ładunku. Na dolny szereg działa też przeciwnie skierowana siła elektryczna o wartości
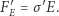 |
(3) |
Zbadajmy, przy jakiej prędkości ładunków te siły równoważą się
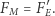 |
(4) |
Obliczmy tę prędkość. Po wstawieniu do (4) wzorów (1), (2) i (3) otrzymujemy
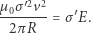 |
(5) |
Natężenie pola elektrycznego dla jednorodnie naładowanego przewodu można obliczyć z prawa Gaussa. Wynosi ono
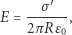 |
(6) |
gdzie 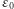 to przenikalność elektryczna próżni.
to przenikalność elektryczna próżni.
Wstawiając (6) do (5) otrzymujemy wzór na szukaną prędkość
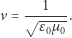 |
(7) |
Przypomnijmy: dla prędkości ładunków danej wzorem (7) siła magnetyczna równoważy siłę elektryczną. Jednak w układzie, w którym ładunki spoczywają, działa na nie tylko siła elektryczna. Zatem w tym układzie nasz szereg ładunków ma przyspieszenie skierowane w dół, a w "primowanym" nie ma żadnego. To jest sprzeczne z zasadą względności Galileusza, zgodnie z którą przyspieszenie cząstki jest takie samo we wszystkich inercjalnych układach odniesienia. Zatem można wyciągnąć wniosek, że niemożliwe jest osiągnięcie przez ładunki elektryczne prędkości danej wzorem (7). Dla przypomnienia - jest to wzór na prędkość światła w próżni.
Do tego wniosku dochodzimy, stosując wyłącznie zwykłą "szkolną" fizykę, nie wiedząc nic o istnieniu teorii względności!
Rozważmy jeszcze dokładniej "realną" sytuację, gdy siła elektryczna z rysunku 3 jest większa od magnetycznej. Siła wypadkowa musi być w obu układach taka sama. Stąd nieuchronny wniosek, że siła 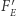 działająca w układzie poruszającym się (Rys. 3) musi być większa od tej w układzie spoczywającym (Rys. 1). Ze wzoru (6) widać, że jest to możliwe, jeśli liniowa gęstość ładunku w układzie poruszającym się
działająca w układzie poruszającym się (Rys. 3) musi być większa od tej w układzie spoczywającym (Rys. 1). Ze wzoru (6) widać, że jest to możliwe, jeśli liniowa gęstość ładunku w układzie poruszającym się 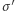 będzie większa od gęstości
będzie większa od gęstości 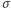 w układzie spoczywającym. Jeśli zakładamy niezmienniczość ładunku, zostaje nam jeszcze jedno wyjście: odległość między ładunkami zależy od ich prędkości. Gdy się poruszają (Rys. 3) - odległość ta jest mniejsza, zatem gęstość liniowa ładunku jest większa.
w układzie spoczywającym. Jeśli zakładamy niezmienniczość ładunku, zostaje nam jeszcze jedno wyjście: odległość między ładunkami zależy od ich prędkości. Gdy się poruszają (Rys. 3) - odległość ta jest mniejsza, zatem gęstość liniowa ładunku jest większa.
Spróbujmy obliczyć to skrócenie odległości. Zauważmy, że
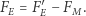 |
(8) |
Podstawiając do (8) wzory (1), (2), (3) i (6) otrzymujemy
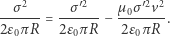 |
Po uproszczeniu i uporządkowaniu możemy napisać
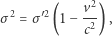 |
gdzie  jest prędkością światła daną wzorem (7).
jest prędkością światła daną wzorem (7).
Przedstawmy tę zależność w postaci
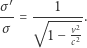 |
Stosunek gęstości liniowej ładunku w obu układach jest równy odwrotnemu stosunkowi odległości między poszczególnymi ładunkami w tych układach. Zatem możemy napisać:
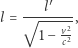 |
(9) |
gdzie 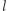 to odległość między ładunkami w układzie spoczywającym, a
to odległość między ładunkami w układzie spoczywającym, a 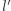 - w układzie poruszającym się. Jest to wzór na tzw. skrócenie Lorentza.
- w układzie poruszającym się. Jest to wzór na tzw. skrócenie Lorentza.
Stosując "nierelatywistyczne" wzory elektrodynamiki i zasadę względności Galileusza, udało się na prostym przykładzie uzasadnić niemożliwość osiągnięcia prędkości światła i w dodatku uzyskać prawidłowy wzór na czysto relatywistyczne skrócenie Lorentza! Jak to możliwe?
Elektrodynamika Maxwella jest de facto teorią relatywistyczną, i dlatego można z niej wysnuć relatywistyczne wnioski. Hendrik Lorentz odkrył skrócenie nazwane później jego nazwiskiem jeszcze przed powstaniem teorii względności, szukając transformacji (też nazwanej jego nazwiskiem) zachowującej postać równań Maxwella przy przejściu do układów poruszających się względem eteru. Jednak dopiero Albert Einstein odkrył uniwersalność i pełny sens transformacji (i skrócenia) Lorentza.
Jak widać, skrócenie Lorentza można łatwo zaobserwować nie tylko przy prędkościach zbliżonych do prędkości światła. Wystarczy zmierzyć siłę między dwoma przewodami z prądem. Mimo iż prędkość dryfu elektronów w przewodniku jest rzędu milimetrów na sekundę, efekty relatywistyczne mają tu decydujące znaczenie.
W pięknej książce Edwarda M. Purcella Elektryczność i magnetyzm można znaleźć opis pola magnetycznego jako efektu relatywistycznego.
 w lewo
w lewo