Nowości z przeszłości

Czy ziemia może podskoczyć albo co się rusza w zegarku

Na pewno pamiętacie z lekcji fizyki na temat trzeciej zasady dynamiki Newtona następujące opowiadanie: "Jeśli ktoś podskoczy, to taka sama siła, jak ta, która wypchnęła go w górę, działa na Ziemię w dół, a zatem i ona się poruszy". Oczywiście, ponieważ Ziemia ma masę 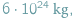$6 ⋅1024 kg;$ a człowiek kilkadziesiąt, nie proponuję Wam, żebyście taki ruch zarejestrowali, jest on na to zbyt mały.

Istnieje jednak zagadnienie dość podobne do powyższego, a mianowicie:

Co się rusza w zegarku?

- Balans, czyli małe kółko poruszające się tam i z powrotem głównie pod wpływem siły sprężystości spiralnej sprężynki, tzw. włosa - powiecie od razu. A co jeszcze? Na pewno kółka zębate, jedne szybciej, inne wolniej. A co jeszcze? Nie wiecie? Cały zegarek, oczywiście jeżeli mu pozwolić. Podobnie jak człowiek odpycha się od Ziemi podskakując, tak balans odpycha się od zegarka i cały zegarek obraca się, za każdym razem w przeciwną stronę. Obraca się bardzo mało, ale przy odpowiedniej metodzie będziemy mogli ten ruch zaobserwować i zmierzyć. Spróbujmy więc odpowiedzieć na pytanie:

Jak wykryć ruch zegarka?

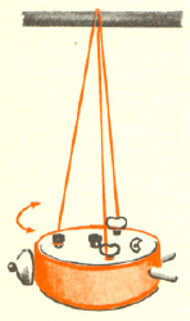
Przede wszystkim trzeba wziąć zegarek. Najwygodniejszy będzie budzik. Musimy teraz pozwolić mu się ruszać. W tym celu zawiesimy go na nitkach, jak na rysunku. Na trzech, bo na jednej kręciłby się ciągle i nic byśmy nie zobaczyli, a na dwóch mógłby ustawić się ukośnie do płaszczyzny poziomej. Przyglądając się zegarkowi nawet bardzo dokładnie, trudno zauważyć jakikolwiek ruch z częstością jego tykania (z taką częstością porusza się balans).

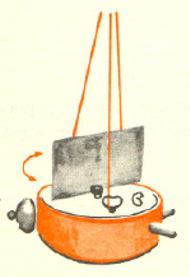
Dla wykrycia jego ruchu dorobimy zegarkowi długą, kilkumetrową wskazówkę z... promienia świetlnego. Jest to metoda stosowana w konstrukcji galwanometrów zwierciadlanych służących do pomiarów bardzo małych prądów. Do zegarka przymocujemy pionowo małe lusterko, jak na rysunku (może być kawałek rozbitego) i oświetlimy je latarką kieszonkową. Obserwując odbitą plamkę świetlną na ścianie (w pokoju nie może być zbyt jasno) można zauważyć, że wykonuje ona drgania, i zmierzyć ich amplitudę. W ten sposób zaobserwowaliśmy "odrzut" zegarka wywołany ruchem balansu. Spróbujmy jednak być fizykami. Kiedy fizyk zaobserwuje jakiejś zjawisko, zwykle zadaje sobie pytanie:

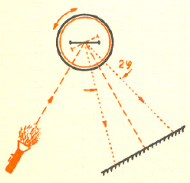
Jakich informacji nam ono dostarcza?

Ruch, który widzieliśmy, jest ilustracją zasady zachowania momentu pędu. Mówi ona, że moment pędu 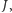$|J,$ równy iloczynowi momentu bezwładności I przez prędkość kątową co, jest wielkością stałą:

J = Iω

pod warunkiem, że na układ nie działają siły zewnętrzne lub działają takie siły, których całkowity moment równa się zeru. Nasz układ składa się z balansu (o momencie bezwładności 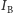$IB$ i prędkości kątowej 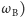$|ω$ i reszty zegarka (o momencie bezwładności 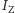$IZ$ i prędkości kątowej 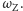$|ω$ Jeżeli układ jako całość ma spoczywać, jego moment pędu musi równać się zeru:

J = IBω

Wynika stąd, że prędkości kątowe balansu i zegarka mają przeciwne znaki i są odwrotnie proporcjonalne do momentów bezwładności:

ω-- = −IZ. ω IB

W ruchu drgającym taki sam będzie stosunek kątów wychyleń balansu i zegarka:

φB-= −IZ φZ IB

Zakładając więc, że amplituda wahań balansu jest rzędu jednego radiana, możemy oszacować stosunek momentów bezwładności na podstawie zmierzonej amplitudy wahań zegarka pamiętając, że kąt obrotu "wskazówki" świetlnej jest dwukrotnie większy od kąta obrotu zwierciadełka.

Okazuje się, że obliczony stosunek momentów bezwładności może nam się jeszcze przydać, analizując bowiem ruch układu możemy na podstawie obliczeń przewidzieć

Nowe zjawisko

Polega ono na tym, że zegarek swobodnie zawieszony "chodzi" szybciej niż nieruchomo zamocowany. Jak wiadomo, w ruchu harmonicznym okres drgań wynosi

√ -- T = 2π I, k

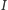gdzie $I$ jest momentem bezwładności, a 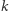$|k$ współczynnikiem sprężystości sprężyny, tj. stosunkiem momentu siły do wychylenia kątowego. W przypadku ruchu względnego dwóch części można wykazać, że efektywny moment bezwładności występujący w powyższym równaniu wyraża się wzorem:

1 = 1-+ 1-, I I1 I2

czyli w naszym przypadku:

I I I = --B-Z- IB + IZ

Oczywiście dla zegarka nieruchomego liczy się tylko moment bezwładności balansu. Jeżeli przeprowadzić rachunek (spróbujcie), to okaże się, że różnica wskazań zegarka swobodnego i nieruchomego 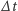$|∆t$ po czasie t spełnia przybliżoną równość

∆t 1IB -t-≈ 2I- Z

(podczas rachunków pamiętamy, że 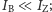$IB ≪ IZ;$ korzystamy też z przybliżenia 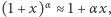$|(1+ x)α≈ 1+ α x,$ słusznego dla 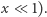$|x≪ 1).$ Zastanówcie się, czy w warunkach Waszego doświadczenia da się tę różnicę zmierzyć, a jeśli tak - spróbujcie. Jak zwykle, czekam na listy z opisem Waszych doświadczeń. A może sami macie pomysły ciekawych eksperymentów do wykonania w domu? Napiszcie!