Poruszają się po krzywych stożkowych, przy czym rodzaj krzywej zależy od całkowitej energii układu. Jeżeli energia jest na tyle mała, że ciała tworzą stan związany, czyli nie mogą się od siebie uwolnić, tylko muszą krążyć wokół siebie, to robią to po elipsach. Jeżeli energia układu jest wystarczająco duża, żeby mogły oddalić się od siebie dowolnie daleko, to najpierw zbliżają się do siebie, a potem uciekają na ogół po hiperbolach, chyba że energia będzie dokładnie na granicy pomiędzy stanem związanym a niezwiązanym, kiedy to będą poruszać się po parabolach.

Zajmijmy się stanem związanym. Ruch po elipsach jest okresowy, co oznacza, że co pewien ustalony okres ciała zajmują te same położenia w przestrzeni. Możemy wyobrazić sobie, że te dwa ciała to np. Ziemia i Słońce albo układ podwójny gwiazd. Jeżeli tylko ciała te mają symetrię sferyczną, to ich ruch jest dokładnie taki sam, jak ruch punktów materialnych o tych samych masach. Teoria Newtona mówi nam, że te dwa ciała będą krążyć po okresowych orbitach dowolnie długo.

A co teoria Newtona powie nam o tym, jak będzie wyglądał ruch trzech ciał? Opis ruchu trzech ciał nie jest już tak prosty i elegancki, jak dla dwóch. Ogólny problem opisu ruchu trzech ciał o porównywalnych masach w teorii Newtona nie ma ogólnego rozwiązania analitycznego. Rozwiązania numeryczne mają cechy chaotyczne, czyli trudno jest przewidzieć zachowanie takiego układu w dłuższej perspektywie czasowej, bo jest ono bardzo czułe na warunki początkowe. Możliwe są zderzenia i ucieczka jednego z ciał kosztem zbliżenia się do siebie dwóch pozostałych. Daleko więc takiemu układowi trzech ciał do elegancji i prostoty układu złożonego tylko z dwóch.

A jak to wygląda w ogólnej teorii względności (OTW)? W teorii Newtona najprostszym obiektem jest masa punktowa, czyli wyidealizowany obiekt, który inaczej niż gwiazda czy planeta nie ma objętości i struktury wewnętrznej. W pewnym sensie najprostszym odpowiadającym mu obiektem w teorii względności jest czarna dziura - obiekt mający tylko masę (i ewentualnie moment pędu lub ładunek elektryczny), przy czym cała jego masa jest skupiona w jednym punkcie, zwanym ze względu na swe zadziwiające własności, osobliwością. Problem jednego ciała, czyli pole grawitacyjne wokół jednej czarnej dziury, został rozwiązany bardzo szybko po sformułowaniu OTW, bo już w roku 1916 jego rozwiązanie zostało opublikowane przez Karla Schwarzschilda. Potem pojawiły się również rozwiązania opisujące naładowaną i wreszcie rotującą czarną dziurę. A co ze stanem związanym dwóch mas? Do tej pory nie znamy ogólnego analitycznego rozwiązania takiego problemu.

Wygląda na to, że w OTW nie potrafimy rozwiązać problemu dwóch ciał, tak jak potrafiliśmy to zrobić w teorii Newtona. Dlaczego tak jest? A może źle liczymy te ciała czy też obiekty fizyczne? Zanim wrócimy do tego pytania, zajmiemy się tym, co wiemy o układzie związanym dwóch mas w OTW. Wiemy, że gdy masy te są wystarczająco daleko od siebie, to ich ruch w niewielkim stopniu odbiega od ruchu po elipsach opisywanego przez teorię Newtona. Jest to szczególny przypadek, którego opis daje się znaleźć za pomocą przybliżonych rachunków, gdzie oblicza się poprawki do orbit newtonowskich pochodzące od OTW, zakładając, że są małe. A na czym te poprawki, czy też małe odstępstwa od orbit newtonowskich, polegają? Okazuje się, że ruch nie jest już idealnie okresowy. Po pierwsze, kierunek wyznaczony przez prostą łączącą punkty, w których ciała są w maksymalnej odległości od siebie, powoli się obraca, a po drugie, ta maksymalna odległość po każdym okrążeniu staje się coraz mniejsza - ciała powoli na siebie spadają. W teorii Newtona rozmiar orbity jest ściśle związany z całkowitą energią układu, która pozostaje stała - gdy jedno ciało zbliża się do drugiego, to rośnie ich energia kinetyczna kosztem energii potencjalnej, a kiedy się oddala, to rośnie energia potencjalna kosztem energii kinetycznej. Im mniejsza energia całkowita, tym ciaśniejsza orbita. Jeżeli więc orbity się zacieśniają, a ciała na siebie spadają, to wygląda na to, że tracona jest energia układu. A co z zasadą zachowania energii?

Ogólna teoria względności ma odpowiedź i na to pytanie. Przewiduje, że energia jest unoszona przez promieniowanie (fale) grawitacyjne. Promieniowanie to unosi nie tylko energię, ale także moment pędu. Dopiero po uwzględnieniu energii (momentu pędu, a także pędu - o czym później) pola grawitacyjnego całkowita energia (moment pędu, pęd) układu jest zachowana. Wygląda więc na to, że problem dwóch orbitujących mas w OTW przestaje być problemem dwóch ciał, ponieważ w opisie musimy uwzględniać trzeci pełnoprawny obiekt niosący energię, pęd i moment pędu, jakim jest pole grawitacyjne. Wygląda to bardziej jak problem trzech ciał i okazuje się, że poza sytuacją, kiedy wpływ OTW stanowi tylko małą poprawkę do ruchu newtonowskiego, nie daje się opisywać w sposób analityczny, podobnie jak problem trzech ciał w teorii Newtona.

Mimo braku ogólnego rozwiązania analitycznego problem trzech ciał w teorii Newtona daje się stosunkowo łatwo symulować numerycznie na komputerze. Okazuje się natomiast, że problem dwóch mas znajdujących się na tyle blisko siebie, że efekty relatywistyczne stają się dominujące i nie można już uznawać ich za małe poprawki do ruchu newtonowskiego, jest problemem niezwykle trudnym do rozwiązania również za pomocą superkomputerów. Spodziewano się, że para czarnych dziur wreszcie na siebie spadnie i stworzy jedną czarną dziurę, jednak przebieg tego zjawiska, pomimo ogromnego wysiłku wielu badaczy, latami wymykał się próbom symulowania na komputerze.

OTW utożsamia grawitację z zakrzywieniem czasoprzestrzeni. Taka krzywa geometria jest opisywana za pomocą funkcji gładkich spełniających układ równań różniczkowych cząstkowych. Czasoprzestrzeń w otoczeniu czarnej dziury, gdzie pole grawitacyjne jest silne, jest bardzo mocno zakrzywiona. Numeryczne modelowanie ewolucji geometrii silnie zakrzywionej czasoprzestrzeni wokół pary czarnych dziur wymaga zastąpienia opisu za pomocą gładkich funkcji przez opis za pomocą wartości tych funkcji w węzłach skończonej dyskretnej sieci. Znalezienie właściwej metody dyskretyzacji równań OTW okazało się zadaniem bardzo trudnym.

Przełom nastąpił dopiero w roku 2005. Wtedy właśnie pojawiły się pierwsze publikacje raportujące udane symulacje trzech faz: spiralnego spadku czarnych dziur na siebie, zlania się pary czarnych dziur w jedną i dochodzenia powstałej nowej czarnej dziury do stanu stacjonarnego. Trudności, które udało się wreszcie przezwyciężyć, były różnego rodzaju. Okazuje się, na przykład, że różne, ale matematycznie równoważne sformułowania ewolucji czasoprzestrzeni w OTW ujawniają bardzo zróżnicowane własności, gdy na ich podstawie próbuje się znaleźć rozwiązania numeryczne. Większość tych sformułowań jest numerycznie niestabilna. Kluczem do sukcesu stało się sformułowanie znane jako metoda BSSN (od nazwisk Baumgarte, Shapiro, Shibata, Nakamura), które obecnie wykorzystuje się do stabilnych numerycznie symulacji. Kolejnym problemem jest fakt, że czarne dziury obecne w symulacji są punktami osobliwymi, co objawia się między innymi tym, że wartości pewnych parametrów mogą być rozbieżne w pobliżu takich punktów. Z problemem tym poradzono sobie, znajdując odpowiednie współrzędne i wykluczając obszar otaczający osobliwość. Pomocny przy tym okazał się fakt, że osobliwości są ukryte pod horyzontem zdarzeń i informacja o tym, co się dzieje w ich otoczeniu, i tak nie wydostaje się na zewnątrz horyzontu. Jeszcze inną komplikacją jest konieczność symulowania dużej objętości przestrzeni wokół układu pary czarnych dziur po to, żeby uwzględnić efekty falowe, ponieważ promieniowanie grawitacyjne odgrywa istotną rolę, unosząc energię i pęd. Z drugiej strony obszary silnych pól w pobliżu czarnych dziur muszą być symulowane z dużą rozdzielczością, żeby zapewnić odpowiednią dokładność i stabilność numeryczną. Ponieważ zasoby nawet najwydajniejszych superkomputerów są ograniczone, nie jest możliwe symulowanie całej dużej objętości z wysoką rozdzielczością, zastosowano więc rozwiązanie polegające na zagęszczaniu sieci, na której prowadzone są obliczenia w otoczeniu czarnych dziur - im bliżej czarnej dziury, tym siatka staje się gęstsza, przy czym zagęszczenia te "śledzą" położenie czarnych dziur, czyli siatka, na której komputer prowadzi obliczenia, zmienia się dynamicznie w czasie symulacji.

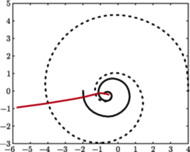
Wynik przykładowej symulacji. Dwie czarne dziury, cięższa (spirala ciągła) i lżejsza (spirala przerywana), zlewają się, tworząc jedną czarną dziurę, która doznaje odrzutu i porusza się w lewo po kolorowej trajektorii z prędkością około 300 km/s.

Jeszcze przed pierwszymi udanymi symulacjami badacze spodziewali się, że dwie czarne dziury spadną na siebie po spiralnych orbitach, zleją się i powstanie jedna czarna dziura. Od symulacji oczekiwali dokładnych ilościowych przewidywań na temat tego, jaka będzie masa i moment pędu powstałej czarnej dziury, a jaka część energii i momentu pędu uleci w postaci promieniowania grawitacyjnego i jak dokładnie to promieniowanie będzie wyglądało. Symulacje dostarczyły odpowiedzi na te pytania dla różnych konfiguracji, różniących się stosunkiem mas czarnych dziur oraz wartościami i kierunkami momentu pędu składników układu podwójnego. Pewnym zaskoczeniem okazała się wartość pędu czarnej dziury powstałej w wyniku zlania się pary czarnych dziur dla pewnych szczególnych konfiguracji. Zjawisko polegające na tym, że powstała w wyniku zlania się niesymetrycznego układu podwójnego czarna dziura uzyskuje niezerowy pęd względem środka masy układu podwójnego przed zderzeniem, nazwano odrzutem grawitacyjnym. Zasada zachowania pędu pozostaje spełniona, ponieważ przeciwny pęd unosi promieniowanie grawitacyjne. Typowe wartości prędkości odrzutu są rzędu setek km/s, ale dla pewnych szczególnych konfiguracji (odpowiednio dobranego stosunku mas składników układu podwójnego i wektorów ich momentów pędu) może sięgać kilku tysięcy km/s, co stanowi wartość przewyższającą prędkość ucieczki nawet z dużych galaktyk. Tak silnego odrzutu się nie spodziewano. Problem znalezienia obserwacji astronomicznych związanych z tym odkryciem pozostaje otwarty.

Dzięki symulacjom numerycznym mamy więc wreszcie pełny obraz tego, jak w teorii zachowuje się układ dwóch czarnych dziur. Takie symulacje są niezwykle ważne z punktu widzenia rodzącej się właśnie nowej dziedziny astronomii - astronomii grawitacyjnej, ponieważ proces zlewania się czarnych dziur jest jednym z potencjalnych źródeł silnego promieniowania grawitacyjnego, które, być może, uda się zarejestrować za pomocą detektorów, które w ostatnich latach zostały do tego celu zbudowane. Jak na razie nie udało się bezpośrednio zarejestrować promieniowania grawitacyjnego, jednak symulacje dostarczają wzorców, które można będzie ewentualnie porównać z sygnałem zarejestrowanym przez detektor wtedy, kiedy do takiej detekcji dojdzie. Obecnie najczulszym detektorem jest Advanced LIGO, który ma zacząć pracę w tym roku, zastępując poprzedni detektor LIGO, od którego ma być dziesięciokrotnie czulszy. LIGO przez 8 lat nasłuchiwania (2002-2010) nie zarejestrował promieniowania grawitacyjnego. Być może teraz Advanced LIGO dostarczy tych przełomowych obserwacji, które byłyby kolejnym wielkim sukcesem przewidywań OTW sto lat po jej opublikowaniu. A może zaskoczy jakąś niespodzianką? Pozostaje czekać na wyniki jego pracy.