Tachiony, czyli absolutna synchronizacja zegarów
Efekt Dopplera dla dźwięku jest powszechnie znanym zjawiskiem. Polega on na zmianie częstotliwości fali dźwiękowej odbieranej przez obserwatora wskutek wzajemnego ruchu źródła i odbiornika dźwięku. Jednak zmiana ta jest całkiem zastanawiająca...

Efekt Dopplera a względność ruchu
Gdy przyjrzymy się uważnie równaniom, okaże się, że jeżeli źródło
dźwięku zbliża się do nieruchomego obserwatora z prędkością
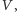 emitując dźwięk o częstotliwości
emitując dźwięk o częstotliwości
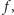 obserwator zarejestruje
częstotliwość
obserwator zarejestruje
częstotliwość
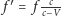 (gdzie
(gdzie
 jest prędkością dźwięku
w nieruchomym powietrzu). Natomiast gdy to obserwator będzie zbliżał
się, z tą samą prędkością, do nieruchomego źródła, częstotliwość
odebrana będzie wyrażona wzorem
jest prędkością dźwięku
w nieruchomym powietrzu). Natomiast gdy to obserwator będzie zbliżał
się, z tą samą prędkością, do nieruchomego źródła, częstotliwość
odebrana będzie wyrażona wzorem
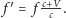 Czy ten wynik nie stoi
w sprzeczności z zasadą względności ruchu? Przecież już w szkole
podstawowej uczono nas, że na zjawiska fizyczne nie powinno mieć wpływu,
który obiekt uznamy za ruchomy, a który potraktujemy jako punkt
odniesienia?
Czy ten wynik nie stoi
w sprzeczności z zasadą względności ruchu? Przecież już w szkole
podstawowej uczono nas, że na zjawiska fizyczne nie powinno mieć wpływu,
który obiekt uznamy za ruchomy, a który potraktujemy jako punkt
odniesienia?
Kluczem do rozwiązania tego problemu jest spostrzeżenie, że w przypadku rozważania ruchu fali dźwiękowej nie wszystkie układy odniesienia są równoprawne. Istnieje pewien układ wyróżniony – jest nim nieruchome powietrze. Wyróżnia go – w sensie fizycznym – fakt, że to właśnie powietrze jest ośrodkiem, w którym porusza się dźwięk. Jeśli układ odniesienia porusza się względem powietrza, ruch ten wpływać musi na prędkość rozchodzenia się dźwięku w tym układzie. A zatem, mierząc prędkość dźwięku w przeciwnych kierunkach, jesteśmy w stanie jednoznacznie stwierdzić, czy i z jaką prędkością poruszamy się względem układu wyróżnionego.
W podobny sposób Michelson i Morley próbowali ustalić, z jaką prędkością Ziemia porusza się względem eteru, hipotetycznego ośrodka, który miał być nośnikiem fal elektromagnetycznych. Jednak ich pomiar pokazał, że prędkość światła jest stała i izotropowa, w efekcie doprowadzając do powstania szczególnej teorii względności (STW) oraz odrzucenia hipotezy eteru. Czy słusznie?
Prędkość dźwięku po drodze otwartej
Zastanówmy się, w jaki sposób można wyznaczyć prędkość dźwięku
w jedną stronę. Niech będzie dana platforma kolejowa o długości
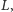 poruszająca się w nieruchomym powietrzu z prędkością
poruszająca się w nieruchomym powietrzu z prędkością
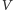 względem torów. Prędkość dźwięku w układzie odniesienia
spoczywającym względem powietrza wynosi
względem torów. Prędkość dźwięku w układzie odniesienia
spoczywającym względem powietrza wynosi
 – jest stała i izotropowa. Na
przeciwległych krańcach platformy umieszczono nadajniki oraz odbiorniki
dźwięku, emitujące i odbierające fale dźwiękowe przesyłane w obydwu
kierunkach.
– jest stała i izotropowa. Na
przeciwległych krańcach platformy umieszczono nadajniki oraz odbiorniki
dźwięku, emitujące i odbierające fale dźwiękowe przesyłane w obydwu
kierunkach.
Przyjmijmy, że
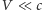 oraz że obserwator na platformie ma znikający
wymiar prostopadły do kierunku jej ruchu (jest dwuwymiarowy). Ruch
powietrza nie będzie więc przez niego wyczuwalny. Dlatego taki obserwator, nie
mając żadnych zewnętrznych punktów odniesienia, nie jest świadom faktu,
że platforma porusza się względem torów ani że powietrze jest ruchome
względem platformy. Czy może mimo wszystko ustalić to, wykonując pomiar
prędkości dźwięku?
oraz że obserwator na platformie ma znikający
wymiar prostopadły do kierunku jej ruchu (jest dwuwymiarowy). Ruch
powietrza nie będzie więc przez niego wyczuwalny. Dlatego taki obserwator, nie
mając żadnych zewnętrznych punktów odniesienia, nie jest świadom faktu,
że platforma porusza się względem torów ani że powietrze jest ruchome
względem platformy. Czy może mimo wszystko ustalić to, wykonując pomiar
prędkości dźwięku?
Światło i dźwięk
Załóżmy na początek, że obserwator na platformie ma do swojej dyspozycji laser.
Ponieważ prędkość światła jest nieporównanie większa od prędkości
dźwięku, może on dokonać w zasadzie absolutnej (natychmiastowej)
synchronizacji zegarów na obu końcach platformy. Wystarczy, że ze środka
platformy wyśle w kierunku obu zegarów impuls światła, ustawiający ich
wskazania na
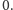 Po zsynchronizowaniu zegarów mierzy czas przelotu fali
dźwiękowej w kierunku ruchu platformy oraz w kierunku przeciwnym
i otrzymuje odpowiednio
Po zsynchronizowaniu zegarów mierzy czas przelotu fali
dźwiękowej w kierunku ruchu platformy oraz w kierunku przeciwnym
i otrzymuje odpowiednio
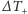 i
i
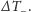 Porównując odczyty
zegarów, wnioskuje, że prędkość dźwięku w kierunkach przeciwnych jest
różna. Używając równań fizyki galileuszowskiej, nasz obserwator szuka
metody ustalenia prędkości platformy względem powietrza. Zapisuje
równania:
Porównując odczyty
zegarów, wnioskuje, że prędkość dźwięku w kierunkach przeciwnych jest
różna. Używając równań fizyki galileuszowskiej, nasz obserwator szuka
metody ustalenia prędkości platformy względem powietrza. Zapisuje
równania:
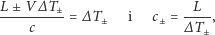 |
gdzie
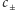 to prędkość dźwięku, odpowiednio, w kierunku ruchu
platformy i w przeciwnym. Rozwiązanie powyższych równań daje:
to prędkość dźwięku, odpowiednio, w kierunku ruchu
platformy i w przeciwnym. Rozwiązanie powyższych równań daje:
 |
Zauważmy, że w tym przypadku:
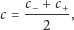 |
czyli prędkość dźwięku w nieruchomym powietrzu jest średnią prędkości
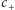 i
i
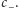

Rys. 1 W nieruchomym powietrzu prędkość dźwięku jest stała i izotropowa, równa
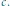 Ruch platformy wpływa na prędkość dźwięku w kierunkach zgodnym i
przeciwnym do jej ruchu, mierzoną w układzie odniesienia związanym z platformą.
Ruch platformy wpływa na prędkość dźwięku w kierunkach zgodnym i
przeciwnym do jej ruchu, mierzoną w układzie odniesienia związanym z platformą.
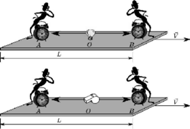
Rys. 2 Synchronizacja zegarów za pomocą światła i dźwięku.
Tylko dźwięk
A jak sobie poradzić, gdy obserwator nie ma do dyspozycji lasera? Może
wówczas użyć jedynie fal dźwiękowych, wiedząc, że prędkość dźwięku
w nieruchomym powietrzu jest stała i izotropowa. Można spróbować
zsynchronizować zegary analogicznie, umieszczając źródło fali pośrodku
(punkt
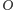 ) platformy i wysyłając sygnał dźwiękowy jednocześnie
w kierunku obu zegarów (nazwijmy je odpowiednio
) platformy i wysyłając sygnał dźwiękowy jednocześnie
w kierunku obu zegarów (nazwijmy je odpowiednio
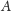 i
i
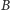 ).
W momencie dotarcia dźwięku do zegara zostaje on ustawiony na czas równy
).
W momencie dotarcia dźwięku do zegara zostaje on ustawiony na czas równy
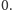 Załóżmy, że (nieznane) prędkości dźwięku w jedną stronę
spełniają zależność:
Załóżmy, że (nieznane) prędkości dźwięku w jedną stronę
spełniają zależność:
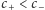 (jak powyżej). Oczywiste jest, że sygnał
dźwiękowy wyemitowany z
(jak powyżej). Oczywiste jest, że sygnał
dźwiękowy wyemitowany z
 do
do
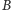 dotrze do celu później
niż z
dotrze do celu później
niż z
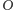 do
do
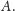 W momencie gdy sygnał dźwiękowy restartuje
zegar
W momencie gdy sygnał dźwiękowy restartuje
zegar
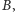 zegar
zegar
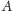 wskazuje:
wskazuje:
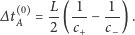 |
Załóżmy, że w chwili, gdy
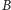 jest zresetowany, sygnał dźwiękowy
zostaje wysłany z
jest zresetowany, sygnał dźwiękowy
zostaje wysłany z
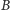 do
do
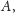 w celu pomiaru prędkości dźwięku
z
w celu pomiaru prędkości dźwięku
z
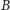 do
do
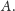 Gdy sygnał ten osiągnie zegar
Gdy sygnał ten osiągnie zegar
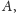 odczyt zegara
będzie równy:
odczyt zegara
będzie równy:
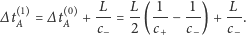 |
Zatem zmierzona prędkość od
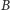 do
do
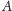 wynosi:
wynosi:
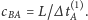 Po elementarnych rachunkach otrzymujemy:
Po elementarnych rachunkach otrzymujemy:
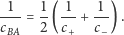 |
Widzimy zatem, że eksperymentalnie zmierzona prędkość w jedną stronę
jest w rzeczywistości średnią harmoniczną prędkości z
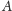 do
do
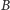 oraz z
oraz z
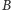 do
do
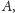 czyli prędkością po drodze zamkniętej
czyli prędkością po drodze zamkniętej
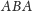 (mierząc prędkość z
(mierząc prędkość z
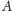 do
do
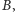 otrzymalibyśmy
identyczny rezultat). Oznacza to, że niemożliwe jest zmierzenie prędkości
otrzymalibyśmy
identyczny rezultat). Oznacza to, że niemożliwe jest zmierzenie prędkości
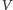 platformy względem torów czy nieruchomego powietrza przy użyciu
jedynie sygnałów dźwiękowych, gdyż nie są one wystarczające do zmierzenia
prędkości dźwięku w jedną stronę
platformy względem torów czy nieruchomego powietrza przy użyciu
jedynie sygnałów dźwiękowych, gdyż nie są one wystarczające do zmierzenia
prędkości dźwięku w jedną stronę
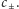 Obserwator, mający do
dyspozycji jedynie falę dźwiękową, nie byłby w stanie eksperymentalnie
zweryfikować, czy porusza się względem ośrodka, w którym ta fala się
rozchodzi (układu preferowanego), czy też nie. Podobnie nie można na
podstawie wyniku doświadczenia Michelsona–Morleya wyciągnąć wniosku,
że układ wyróżniony nie istnieje. Dysponując jedynie falami świetlnymi, nie
możemy tego zweryfikować, a wszystkie pomiary prędkości światła są de
facto pomiarami po drodze zamkniętej.
Obserwator, mający do
dyspozycji jedynie falę dźwiękową, nie byłby w stanie eksperymentalnie
zweryfikować, czy porusza się względem ośrodka, w którym ta fala się
rozchodzi (układu preferowanego), czy też nie. Podobnie nie można na
podstawie wyniku doświadczenia Michelsona–Morleya wyciągnąć wniosku,
że układ wyróżniony nie istnieje. Dysponując jedynie falami świetlnymi, nie
możemy tego zweryfikować, a wszystkie pomiary prędkości światła są de
facto pomiarami po drodze zamkniętej.
Podsumowanie
Czy Natura wybrała układ wyróżniony? Odpowiedź na to pytanie jest na razie nieznana, choć istnieją przesłanki świadczące o tym, że może tak być. Kolejne pytanie, jakie się pojawia, brzmi: czy Natura dała nam narzędzia, dzięki którym możemy to zweryfikować? Aby znaleźć układ wyróżniony, trzeba dokonać pomiaru prędkości światła w przynajmniej dwóch kierunkach. Nie da się tego zrobić, mając do dyspozycji jedynie sygnały świetlne (lub obiekty poruszające się z prędkościami mniejszymi lub równymi prędkości światła). Jednak gdyby istniały tachiony, hipotetyczne cząstki nadświetlne, mogłyby one zostać wykorzystane do absolutnej (natychmiastowej) synchronizacji zegarów z dowolną dokładnością i pomiaru prędkości światła po drodze otwartej. Spełniałyby one podobną rolę jak wiązka światła laserowego przy pomiarze prędkości dźwięku w ruchomym powietrzu. Czy tachiony istnieją? Na to pytanie na razie również nie znamy odpowiedzi. Ale czy Natura byłaby na tyle złośliwa, by dać nam zjawisko bez narzędzi do jego zbadania?
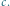 Ruch platformy wpływa na prędkość dźwięku w kierunkach zgodnym i
przeciwnym do jej ruchu, mierzoną w układzie odniesienia związanym z platformą.
Ruch platformy wpływa na prędkość dźwięku w kierunkach zgodnym i
przeciwnym do jej ruchu, mierzoną w układzie odniesienia związanym z platformą.