No właśnie – dociera, ale czy aby na pewno? Nasuwa się pytanie, czy Jaś ma szansę dostać się do zamku olbrzyma, jeżeli prędkość jego wspinaczki jest dużo, dużo mniejsza niż tempo rośnięcia fasoli. Rozważmy następujący model fizyczny sytuacji, przedstawiony za pomocą zadania:

Nieskończenie rozciągliwa guma ma jeden koniec przyczepiony do ściany, drugi zaś jest ciągnięty z prędkością 1 m/s. Początkowo guma ma 1 m długości. Robak, początkowo będący przy ścianie, zaczyna pełznąć wzdłuż gumy z prędkością 0,001 cm/s. Czy robak kiedykolwiek dotrze do końca gumy? Jeśli tak, to po jakim czasie?

Rozwiązanie dla informatyka

Na początek przeformułujemy zadanie tak, by dało się ono opisać jako sekwencja skończonej liczby prostych kroków. W tym celu wyobrazimy sobie, że, zamiast pełznąć jednostajnie wzdłuż gumy, robak odczekuje sekundę, patrząc na rozciągającą się gumę, po czym wykonuje natychmiastowy skok do miejsca, gdzie znalazłby się po kolejnej sekundzie, gdyby guma się nie rozciągała. W miejscu tym czeka cierpliwie przez sekundę, podczas kiedy guma się wydłuża, a następnie wykonuje kolejny skok  Przy takim ruchu robak porusza się nieco wolniej, niżby wynikało to z treści zadania – w porównaniu z robakiem pełznącym jednostajnie prawie zawsze znajduje się bliżej ściany, gdzie prędkości punktów gumy są mniejsze. Oznacza to, że schemat skokowego ruchu robaka opisany powyżej może dać nam górne oszacowanie na czas ruchu robaka.

W czasie jednej sekundy robak przeskakuje o 0,001 cm, a guma wydłuża się o 1 metr. Oznaczając przez  odległość robaka od ściany po upływie  sekund, z powyższych rozważań otrzymujemy wzór rekurencyjny

Rozwijając ten wzór, mamy kolejno

i tak dalej. Ostatecznie otrzymujemy wzór

Suma po prawej stronie równości, czyli logarytm harmoniczny, zawiera się w przedziale  Po 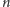-tym kroku długość gumy wynosi  metrów, więc robak na pewno osiągnie koniec gumy, gdy po raz pierwszy zajdzie

A zatem robak osiągnie koniec gumy po czasie  sekund. Zagadnienie znalezienia oszacowania dolnego pozostawiamy Czytelnikowi Wnikliwemu.

Rozwiązanie dla matematyka

Informatykowi wygodnie jest myśleć, że robak porusza się skokami (co trochę fałszuje wynik). Dzięki temu w każdym przedziale czasowym ma skończenie wiele obserwacji – skoków robaka. Takie podejście, w pewnym uproszczeniu, pozwala wytłumaczyć problem komputerowi i oczekiwać od niego przybliżonego rozwiązania. Matematyk może myśleć o tym zagadnieniu podobnie, ale trochę bardziej abstrakcyjnie. Zamiast szukać dobrych przybliżeń rozwiązania przez zmuszanie robaka do skoków z coraz większą częstotliwością, wprowadza abstrakcyjne nieskończenie małe przedziały czasu. Niech 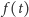 oznacza odległość robaka od ściany w chwili 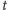 przy założeniu, że guma nie jest rozciągana. Będzie nas interesowało, jak daleko robak może zajść w nieskończenie małym przedziale czasu. Tę wartość, oznaczaną przez 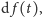 możemy opisać po prostu jako różnicę

Wielkość 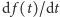(inaczej 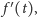 czyli pochodna funkcji ) intuicyjnie ma wyrażać, jak daleko może przesunąć się robak w jednostce czasu, czyli opisuje jego prędkość.

Przyda nam się wynikające z powyższych uwag spostrzeżenie, że

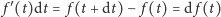(1)

(analogiczny wzór możemy zapisać dla dowolnej funkcji zależnej od parametru ).

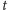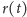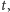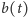Niech  oznacza długość rozciąganej gumy w chwili  a   odległość robaka od ściany, gdy pełznie po rozciąganej gumie. Wtedy dla nieskończenie małego przedziału czasu 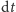 mamy

Wynika to z faktu, iż odległość po czasie 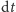 jest równa poprzedniej odległości pomnożonej przez „współczynnik wydłużenia” gumy plus odległość, jaką przebywa w tym czasie sam robak. (Czy widać podobieństwo między tym wzorem a wzorem z rozwiązania informatycznego?)

Korzystając ze wzoru (1), możemy zapisać nasze równanie w postaci

a następnie uprościć lewą stronę

Udało nam się opisać funkcję 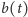 za pomocą równania zawierającego jej pochodną, czyli otrzymaliśmy równanie różniczkowe. Rozwiązaniem tego równania różniczkowego z warunkiem 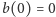 jest

Można to łatwo sprawdzić, różniczkując powyższe równanie, ale lepiej przekonać się o jego sensowności, patrząc na rozwiązanie informatyczne. Warto przy tym pamiętać, że matematyk może myśleć o całce jako o sumie, po odcinkach z nieskończenie drobnego podziału przedziału 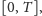 wartości funkcji wybranych z poszczególnych odcinków pomnożonych przez długość odcinków (czyli 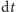). W chwili, gdy robak dotrze do końca gumy po czasie 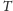(mamy wtedy równość 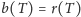), otrzymujemy zależność

Rozwiązanie tego równania ze względu na 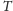(jeśli istnieje) daje odpowiedź w ogólnym przypadku. Podstawmy teraz dane z początkowego zadania: 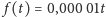 oraz 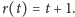 Mamy

lub, pozbywając się całki,

Wobec tego 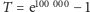 sekund.

Rozwiązanie dla fizyka

Przyjmijmy za początek układu współrzędnych koniec gumy przymocowany do ściany. Niech początkowa długość nierozciągniętej gumy wynosi 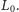 Prawy koniec gumy porusza się z prędkością 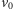 tak, że znajduje się on po czasie 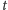 w odległości 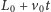 od ściany. Robak porusza się z prędkością  względem fragmentu gumy, na którym się aktualnie znajduje. Jednak dla nieruchomego obserwatora jego prędkość jest większa, gdyż również ten fragment gumy porusza się względem obserwatora (i to w dodatku tym szybciej, im dalej fragment ten znajduje się od zamocowanego końca gumy). Nieruchomy obserwator dostaje zatem następujące równanie na prędkość robaka 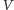 w związanym z nim układzie (przy czym 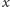 to jego aktualne położenie):

z warunkiem początkowym 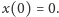 Wyraźnie widać, że gdy robak przemieszcza się w prawo (względem wciąż nieruchomego obserwatora), jego prędkość 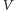 wzrasta. W pewnym momencie jest większa od 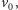 a zatem dystans między robakiem a prawym końcem gumy zaczyna się zmniejszać. Można pokazać (patrz np. rozwiązanie dla matematyka), że zależność położenia od czasu prowadząca do powyższego wzoru to

Porównując położenie 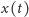 z długością gumy 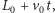 dostajemy czas, po którym robak osiągnie drugi koniec gumy

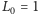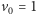Podstawiając  m,  m/s i 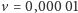  m/s, otrzymujemy 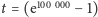 s. Wynik jest o bardzo wiele rzędów wielkości większy niż czas pozostały do wypalenia się Słońca (z grubsza 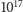 s) czy nawet obecny wiek Wszechświata (nieprzekraczający 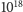 s). Fizyk uzna zatem, że robak nie osiągnie nigdy (tj. w żadnej przewidywalnej przyszłości) końca gumy, a matematyk doda zapewne, że to wszystko dlatego, iż logarytm jest bardzo powoli rosnącą funkcją. Czytelnikowi Wnikliwemu pozostawiamy sprawdzenie, jak szybko robak musiałby się poruszać, by osiągnąć koniec gumy np. przed początkiem tegorocznej wiosny. A czy miałby na to jakiekolwiek szanse, gdyby guma rozciągała się w sposób jednorodny, ale z niewielkim przyspieszeniem?

Morał

(…) Jaś kradnie z zamku olbrzyma kurę znoszącą złote jajka oraz harfę przynoszącą zdrowie i dobre samopoczucie, dzięki czemu Jaś i matka wiodą od tego czasu spokojne i dostatnie życie, głosząc na prawo i lewo, że szczęście sprzyja wytrwałym.

Posłowie dla kosmologa

Opisana w bajce o Jasiu i magicznej fasoli sytuacja jest doskonałą metaforą dla nietypowego (i nierealistycznego) modelu Wszechświata, pozbawionego jakiejkolwiek materii i którego powierzchnie stałego czasu są trójwymiarowymi uogólnieniami powierzchni siodłowej – przestrzeniami o stałej ujemnej krzywiźnie. Zgodnie z ogólną teorią względności taki Wszechświat, podobnie jak łodyga magicznej fasoli, rozszerza się jednorodnie ze stałą prędkością. Zgodnie zaś z morałem bajki, gdyby we Wszechświecie tym mógł się znaleźć jakiś odważny i cierpliwy kosmonauta, mógłby on dolecieć z jednego miejsca we Wszechświecie w dowolne inne pod warunkiem zarezerwowania na ten cel dostatecznie długiego czasu.

Napływ coraz dokładniejszych danych obserwacyjnych spowodował, że najbardziej rozpowszechniony dziś obraz Wszechświata jest całkiem inny. Wskutek występowania zagadkowej energii próżni Wszechświat rozszerza się z przyspieszeniem. Oznacza to, że miejsca Wszechświata dostatecznie dalekie od Ziemi oddalają się od niej z prędkością większą od prędkości światła w próżni i będą oddalać się jeszcze szybciej, nie będą zatem mogły zostać osiągnięte nawet przez najszybsze statki kosmiczne i najwytrwalszych kosmonautów. Z kolei, jeżeli, puściwszy wodze wyobraźni, znajdziemy się we Wszechświecie różniącym się od naszego brakiem energii próżni, taki Wszechświat będzie rozszerzał się z opóźnieniem i do wszystkich jego miejsc można będzie dolecieć w czasie wyrażającym się pewną potęgą odległości do tych miejsc, a więc w praktyce znacznie krótszym, niż gdy rozwiązanie opisywane jest funkcją wykładniczą, jak w rozwiązaniu zagadnienia z bajki.

Krzysztof Turzyński