Rzeczywiście, z punktu widzenia obserwatora zewnętrznego upływ czasu w układzie Roberta Korzeniowskiego (wielkości w tym układzie oznaczać będziemy literkami z primem) jest powolniejszy. Tempo upływu czasu różni się o czynnik 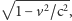gdzie 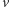jest prędkością chodu. Nie oznacza to jednak, że można przez tenże czynnik skalować prędkości wszystkich ruchów w poruszającym się układzie! Prawo „spowolnionego upływu czasu” o podany czynnik dotyczy obiektów nieruchomych (na przykład zegarów) w poruszającym się układzie odniesienia. Działa ono dobrze również dla obiektów poruszających się powoli w układzie primowanym. Ponieważ jednak ruch nóg w układzie primowanym musi być równie szybki jak ruch piechura, musimy dokonać transformacji Lorentza współrzędnych określających położenie nóg oraz środka masy chodziarza niezależnie. W tym celu wprowadzimy najprostszy z możliwych model chodu.

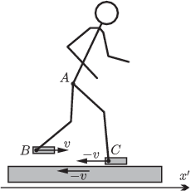
W całym problemie ważne są naprawdę tylko trzy punkty: środek masy 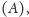i położenie dwóch stóp ( 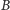 i 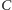). Rozważmy sytuację z punktu widzenia Roberta Korzeniowskiego (czyli w układzie primowanym). Przedstawia ją rysunek  obok.

W tym układzie środek masy 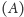jest nieruchomy, chodnik porusza się do tyłu z pewną prędkością 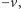stopa aktualnie dotykająca ziemi 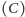również porusza się z prędkością 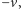a druga stopa, przenoszona do przodu 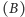porusza się z prędkością 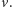Zgodnie z przepisami chodu sportowego w każdej chwili co najmniej jedna stopa musi dotykać ziemi. Dlatego Robert Korzeniowski chcąc iść jak najszybciej, stawiając jedną stopę jednocześnie odrywa drugą. Powiedzmy, że w chwili 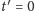stopa odrywana znajduje się 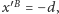w punkcie a stopa stawiana w punkcie 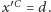 Natomiast przez cały czas środek masy 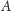znajduje się w punkcie 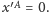Zmiana stóp następuje w chwili 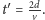Przez następne 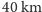 ruch jest cyklicznie powtarzany.

Jak wygląda chód z punktu widzenia obserwatora stojącego na chodniku (układ nieprimowany), dla którego środek masy Roberta Korzeniowskiego porusza się zgodnie z równaniem 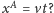 Sprawdźmy najpierw za pomocą transformacji Lorentza, jak wyglądają czasoprzestrzenne współrzędne opisujące stawianie i odrywanie stóp. Rozpocznijmy od pierwszego tupnięcia: stopa 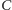postawiona zostaje w punkcie

a stopa 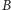oderwana w punkcie

czyli krok staje się dłuższy. Okazuje się jednak, że stopy są stawiane i odrywane w różnych chwilach: stopa 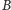zostaje oderwana w chwili

jeszcze zanim zostanie postawiona stopa 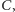co ma miejsce w chwili

(nawiasem mówiąc może to być przyczyną dyskwalifikacji Roberta Korzeniowskiego, mimo iż ten twierdzi, że stopy zmieniał jednocześnie). Rozważmy teraz drugie tupnięcie, w którym stopa 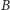zostaje postawiona w punkcie

a stopa 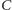oderwana w punkcie

zatem krok jest znowu dłuższy. Odpowiednie chwile odpowiadające tym zdarzeniom to

oraz

Następnie proces powtarzany jest cyklicznie. Sprawdźmy teraz, że czas oderwania stopy od ziemi wynosi:

natomiast czas, w którym druga stopa dotyka ziemi, to:

Możemy teraz odpowiedzieć już w pełni na pytanie, co dzieje się z nogami podczas relatywistycznego chodu według naszego prostego modelu. Czas trwania pełnego kroku, w którym stopa jest przenoszona, a następnie spoczywa na ziemi, wynosi:

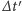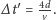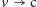i jest dłuższy od czasu  widzianego przez Roberta Korzeniowskiego: Zatem odpowiedź na pytanie, czy im szybciej idziemy, tym wolniej ruszamy nogami, dla zewnętrznego obserwatora jest, paradoksalnie, twierdząca! W granicy czas trwania pełnego kroku staje się wręcz nieskończony! Jest i druga ciekawa obserwacja: w tej granicy obie stopy przez większość czasu „fruną w powietrzu”, robiąc ogromne kroki i prawie wcale nie dotykając ziemi.

To ostatnie stwierdzenie staje się wręcz oczywiste, gdy zdamy sobie sprawę, że w układzie Roberta Korzeniowskiego cały zewnętrzny świat (zatem również chodnik) się skraca. I mimo że długość kroku według Korzeniowskiego jest zwyczajna, to skracanie chodnika powoduje, iż każdy krok wiąże się z pokonaniem ogromnego dystansu. Nic więc dziwnego, że z punktu widzenia sędziów kroki piechura stają się nienaturalnie długie. Ponieważ jednak nogi Korzeniowskiego nie mogą się wydłużać, to jedyną możliwością zrealizowania tej sytuacji jest bieg z wydłużoną fazą lotu.