Ukryty pęd

Rys. 1 Schemat rozważanego układu przewodzących walców.
Przy omawianiu elektryczności i magnetyzmu w uniwersyteckim kursie fizyki definiuje się wielkość zwaną wektorem Poyntinga:
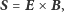 | (1) |
którą interpretuje się np. jako gęstość pędu pola elektromagnetycznego
mnożoną przez czynnik
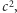 gdzie
gdzie
 jest prędkością światła
w próżni. Oznacza to, że pęd niesiony przez pole w ustalonym fragmencie
przestrzeni można obliczyć, całkując
jest prędkością światła
w próżni. Oznacza to, że pęd niesiony przez pole w ustalonym fragmencie
przestrzeni można obliczyć, całkując
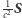 po tym właśnie fragmencie.
Jak się zaraz przekonamy, prowadzi to do zastanawiających wyników.
po tym właśnie fragmencie.
Jak się zaraz przekonamy, prowadzi to do zastanawiających wyników.

Rys. 2 Przekrój poprzeczny przez rozważany układ przewodzących walców.
Rozważmy dwa długie, przewodzące, koncentryczne walce o promieniach
 i
i
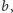 przy czym
przy czym
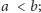 walec wewnętrzny naładowany jest
liniową gęstością ładunku
walec wewnętrzny naładowany jest
liniową gęstością ładunku
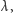 a zewnętrzny liniową gęstością
a zewnętrzny liniową gęstością
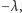 przez oba walce płynie prąd elektryczny o natężeniu
przez oba walce płynie prąd elektryczny o natężeniu
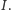 Układ
taki przedstawiony jest schematycznie na rysunku 1. Zgodnie z prawem
Gaussa, pomiędzy walcami występuje pole elektryczne o natężeniu
Układ
taki przedstawiony jest schematycznie na rysunku 1. Zgodnie z prawem
Gaussa, pomiędzy walcami występuje pole elektryczne o natężeniu
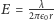 skierowane na zewnątrz osi walców oraz, zgodnie z prawem
Ampère’a, pole magnetyczne o indukcji
skierowane na zewnątrz osi walców oraz, zgodnie z prawem
Ampère’a, pole magnetyczne o indukcji
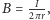 prostopadłe zarówno
do pola elektrycznego, jak i do osi walców (Rys. 2); wewnątrz mniejszego walca
oraz na zewnątrz większego pola są równe zeru. Wykorzystując wzór (1),
nietrudno znaleźć pęd pola elektromagnetycznego w omawianym układzie –
jest on równy
prostopadłe zarówno
do pola elektrycznego, jak i do osi walców (Rys. 2); wewnątrz mniejszego walca
oraz na zewnątrz większego pola są równe zeru. Wykorzystując wzór (1),
nietrudno znaleźć pęd pola elektromagnetycznego w omawianym układzie –
jest on równy
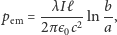
gdzie
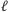 jest długością walców, i skierowany wzdłuż osi walców.
Kierunek i zwrot tego pędu pokrywa się z kierunkiem przepływu prądu
w wewnętrznym walcu.
jest długością walców, i skierowany wzdłuż osi walców.
Kierunek i zwrot tego pędu pokrywa się z kierunkiem przepływu prądu
w wewnętrznym walcu.
Tu pojawia się pewien problem. Jeśli układ walców spoczywa, to jego pęd jest równy zeru. Jak widzimy, pęd pola elektromagnetycznego jest różny od zera, a zatem w układzie powinno być „coś”, czego pęd ma taką samą długość i kierunek, a przeciwny zwrot. Czyli co?
Rozszyfrowanie tej zagadki wymaga zastanowienia się, jaka jest mikroskopowa
natura źródeł pola elektrycznego i magnetycznego – czyli prądu elektrycznego
i gęstości ładunku na walcach. Wyobraźmy sobie (perwersyjnie), że prąd
polega na przepływie elementarnych ładunków dodatnich
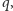 których
liczba w wewnętrznej i zewnętrznej części kabla to odpowiednio
których
liczba w wewnętrznej i zewnętrznej części kabla to odpowiednio
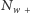 oraz
oraz
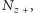 a niezerowa gęstość ładunku zapewniana jest
przez obecność odpowiedniej liczby nieruchomych ładunków ujemnych
a niezerowa gęstość ładunku zapewniana jest
przez obecność odpowiedniej liczby nieruchomych ładunków ujemnych
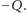 Ładunki
Ładunki
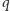 poruszają się z prędkościami odpowiednio
poruszają się z prędkościami odpowiednio
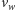 i
i
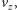 zatem:
zatem:
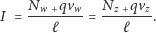 | (2) |
Przy przejściu z wewnętrznej części przewodu na zewnętrzną energia
ładunku
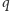 zmienia się z
zmienia się z
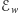 na
na
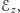 które są związane
zależnością:
które są związane
zależnością:
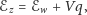 | (3) |
gdzie
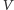 jest różnicą potencjałów elektrostatycznych zewnętrznego
i wewnętrznego walca. Zgodnie ze szczególną teorią względności energia ciała
o masie spoczynkowej
jest różnicą potencjałów elektrostatycznych zewnętrznego
i wewnętrznego walca. Zgodnie ze szczególną teorią względności energia ciała
o masie spoczynkowej
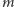 i prędkości
i prędkości
 w inercjalnym układzie
odniesienia wynosi
w inercjalnym układzie
odniesienia wynosi
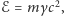 gdzie
gdzie
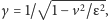 a pęd tego
ciała to
a pęd tego
ciała to
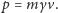 Uzbrojeni w tę wiedzę możemy obliczyć wypadkowy
pęd ładunków krążących w obwodzie (znak
Uzbrojeni w tę wiedzę możemy obliczyć wypadkowy
pęd ładunków krążących w obwodzie (znak
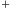 oznacza ruch zgodny
z kierunkiem prądu):
oznacza ruch zgodny
z kierunkiem prądu):
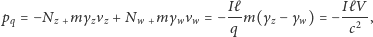 | (4) |
przy czym w obliczeniach skorzystaliśmy najpierw z (2), a następnie z (3).
Ponieważ w opisanym układzie
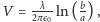 otrzymujemy:
otrzymujemy:
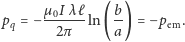
Suma pędu pola elektromagnetycznego oraz tzw. pędu ukrytego, czyli sumy pędów ładunków składających się na prąd elektryczny, jest zatem równa zeru!
Na pierwszy rzut oka może wydać się nieco dziwne, że do wyjaśnienia, dlaczego niezbyt skomplikowany układ przewodników z prądem może spoczywać, musieliśmy odwołać się do szczególnej teorii względności. Zaskoczenie nie powinno jednak trwać długo – przecież teoria ta została sformułowana przez Einsteina właśnie w celu podania praw ruchu zgodnych z prawami elektryczności i magnetyzmu.
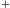 i
i

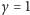 w definicji pędu;
wówczas, oczywiście, wyrażenie dane równaniem (4) jest równe
zeru.
w definicji pędu;
wówczas, oczywiście, wyrażenie dane równaniem (4) jest równe
zeru.