Efekty relatywistyczne w zasięgu ręki?
Prędkość
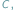 nazywana prędkością światła, jest równa
nazywana prędkością światła, jest równa
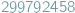 m/s. Dokładnie, bo metr jest zdefiniowany za jej pomocą
i z wykorzystaniem wzorca sekundy. To, w porównaniu z prędkościami,
których doświadczamy, bardzo, bardzo dużo. Na przykład samolot
myśliwski o długości 10 metrów, lecący z prędkością
m/s. Dokładnie, bo metr jest zdefiniowany za jej pomocą
i z wykorzystaniem wzorca sekundy. To, w porównaniu z prędkościami,
których doświadczamy, bardzo, bardzo dużo. Na przykład samolot
myśliwski o długości 10 metrów, lecący z prędkością
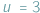 km/s,
skróci się lorentzowsko przez czynnik
km/s,
skróci się lorentzowsko przez czynnik
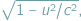 czyli o pięć
angstremów, a więc długość odpowiadającą pojedynczej cząsteczce paliwa
lotniczego.
czyli o pięć
angstremów, a więc długość odpowiadającą pojedynczej cząsteczce paliwa
lotniczego.
Jak widać, mierzalne efekty relatywistyczne wydają się dla zwykłego śmiertelnika nieobserwowalne.
A jednak, podobnie jak monsieur Jourdain nie zdawał sobie sprawy, że mówi prozą, tak my możemy nie wiedzieć, że efekty relatywistyczne własnoręcznie wielokrotnie badaliśmy.
Zacznijmy od eksperymentu myślowego. Wyobraźmy sobie dwa bardzo długie,
położone bardzo blisko siebie i bardzo wąskie taśmociągi, poruszające się
przeciwbieżnie z prędkościami
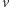 i
i
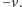 Na taśmociągach
umocowane są, w jednakowych odstępach
Na taśmociągach
umocowane są, w jednakowych odstępach
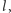 ładunki
ładunki
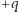 na
tym poruszającym się w prawo oraz
na
tym poruszającym się w prawo oraz
 na tym poruszającym
się w lewo. Liniowa gęstość ładunku taśmociągów wynosi więc
na tym poruszającym
się w lewo. Liniowa gęstość ładunku taśmociągów wynosi więc
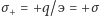 oraz
oraz
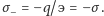 Z odpowiednio dużej
odległości
Z odpowiednio dużej
odległości
 taśmociągi są równoważne prądowi o sumarycznej
gęstości liniowej
taśmociągi są równoważne prądowi o sumarycznej
gęstości liniowej

Następnie umieśćmy, w odległości
 od tak skonstruowanego
„przewodnika” z prądem, spoczywający
od tak skonstruowanego
„przewodnika” z prądem, spoczywający
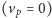 ładunek próbny
ładunek próbny
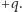 Na ładunek ten nie będzie działać żadna siła ze strony
„przewodnika”, bo sumaryczna liniowa gęstość ładunku jest, z konstrukcji,
zerowa.
Na ładunek ten nie będzie działać żadna siła ze strony
„przewodnika”, bo sumaryczna liniowa gęstość ładunku jest, z konstrukcji,
zerowa.
A teraz spójrzmy na tę sytuację z układu, który porusza się w prawo
z prędkością
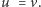 W układzie tym dodatnio naładowany taśmociąg
spoczywa. Ponieważ prędkości taśmociągów są niewielkie, to spróbujmy
opisać tę sytuację za pomocą transformacji Galileusza. Zgodnie z nią
prędkości po prostu się dodają. Wtedy ujemnie naładowany taśmociąg porusza
się z prędkością
W układzie tym dodatnio naładowany taśmociąg
spoczywa. Ponieważ prędkości taśmociągów są niewielkie, to spróbujmy
opisać tę sytuację za pomocą transformacji Galileusza. Zgodnie z nią
prędkości po prostu się dodają. Wtedy ujemnie naładowany taśmociąg porusza
się z prędkością
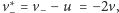 a więc sumaryczna gęstość prądu
wynosi tyle samo co poprzednio (natężenie prądu nienaładowanego
przewodnika jest niezmiennikiem transformacji Galileusza):
a więc sumaryczna gęstość prądu
wynosi tyle samo co poprzednio (natężenie prądu nienaładowanego
przewodnika jest niezmiennikiem transformacji Galileusza):

Gęstość ładunku również nie ulega zmianie, bo transformacja Galileusza na nią nie wpływa.
Ponieważ jednak ładunek próbny porusza się obecnie z prędkością
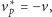 więc okazuje się, że działa na niego siła (odpychająca, tak jak
między przewodnikami o przeciwnych kierunkach prądu):
więc okazuje się, że działa na niego siła (odpychająca, tak jak
między przewodnikami o przeciwnych kierunkach prądu):

Nie jest dobrze. Rozpatrywane układy są inercjalne. Jeśli w jednym nie działa siła, to (w zgodzie z doświadczeniem) w drugim także działać nie może.
Spróbujmy temu zaradzić za pomocą transformacji Lorentza. Zgodnie z nią
prędkości dodają się trochę inaczej. Jeżeli układ primowany porusza się
względem nieprimowanego z prędkością
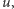 to (równoległa do
to (równoległa do
 i skierowana w tę samą stronę) prędkość
i skierowana w tę samą stronę) prędkość
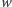 w układzie
nieprimowanym przejdzie na
w układzie
nieprimowanym przejdzie na

Oprócz tego poruszające się (względem jakiegoś układu inercjalnego)
z prędkością
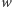 ciała ulegają skróceniu (w tym układzie) o czynnik
ciała ulegają skróceniu (w tym układzie) o czynnik

wzdłuż kierunku ruchu, co w naszym przypadku powoduje wzrost gęstości
liniowej ładunku o czynnik
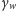 (bo skracający się odstęp
(bo skracający się odstęp
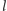 jest
w mianowniku).
jest
w mianowniku).
Teraz należy uważać (ale tylko przez chwilę). Jeżeli popatrzymy na
taśmociąg z układu, w którym taśmociąg spoczywa, to zmierzymy gęstość
ładunku
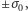 która z gęstością ładunku
która z gęstością ładunku
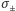 w układzie
początkowym (tym opisanym na początku) jest związana warunkiem
w układzie
początkowym (tym opisanym na początku) jest związana warunkiem
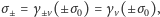 natomiast gęstość prądu warunkiem
natomiast gęstość prądu warunkiem
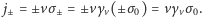 Oczywiście, musi to być prawda dla
dowolnej prędkości
Oczywiście, musi to być prawda dla
dowolnej prędkości
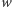 poruszania się danego taśmociagu (tu dla
dodatnio naładowanego):
poruszania się danego taśmociagu (tu dla
dodatnio naładowanego):

Bezpośrednim rachunkiem można sprawdzić następujące równości:

Łatwo wtedy wykazać (podstawiając i porządkując), że pod wpływem
opisanych wyżej transformacji z układu początkowego do układu poruszającego
się z względną prędkością
 (układu primowanego), kombinacja
(układu primowanego), kombinacja
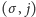 przekształca się analogicznie do kombinacji czasu i położenia
przekształca się analogicznie do kombinacji czasu i położenia
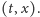

Dzięki temu możemy dokładną analizę zaaranżowanej sytuacji pozostawić
Czytelnikowi i po prostu (znając
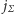 oraz
oraz
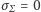 ) obliczyć
sumaryczną gęstość (liniową) ładunku oraz sumaryczną gęstość (liniową)
prądu w układzie primowanym:
) obliczyć
sumaryczną gęstość (liniową) ładunku oraz sumaryczną gęstość (liniową)
prądu w układzie primowanym:

co daje następujące wartości siły elektrycznej
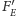 (przyciągającej dla
(przyciągającej dla
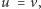 bo
bo
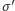 jest wtedy ujemne) oraz siły magnetycznej
jest wtedy ujemne) oraz siły magnetycznej
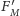 (odpychającej, jak poprzednio):
(odpychającej, jak poprzednio):

gdzie
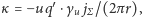 a
a
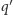 jest wartością ładunku
próbnego w układzie primowanym (nie musimy wnikać w to, jaka jest jego
wartość). Siły te się znoszą, o ile
jest wartością ładunku
próbnego w układzie primowanym (nie musimy wnikać w to, jaka jest jego
wartość). Siły te się znoszą, o ile
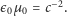 To, dla wychowanych na
układzie SI, nie musi być oczywiste, ale przecież przenikalności dielektryczna
To, dla wychowanych na
układzie SI, nie musi być oczywiste, ale przecież przenikalności dielektryczna
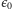 i magnetyczna
i magnetyczna
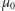 próżni to tylko przeliczniki jednostek
właśnie przez tę relację zdefiniowane!
próżni to tylko przeliczniki jednostek
właśnie przez tę relację zdefiniowane!
Uzmysławiamy sobie w ten sposób, że elektromagnetyzm klasyczny jest teorią relatywistyczną. Wszelkie klasyczne efekty magnetyczne można wyjaśnić za pomocą szczególnej teorii względności. Paradoksalnie jednak, takie proste rozważania sprawdzają się tylko dla niewielkich prędkości (dopóki można nie uwzględniać efektów związanych ze skończoną prędkością światła).
Efekty magnetyczne są mierzalne, bo oddziaływanie elektromagnetyczne jest dużo silniejsze niż grawitacyjne, które determinuje naszą codzienną wrażliwość, oraz dlatego, że dość łatwo zaaranżować sytuację, w której ładunki się poruszają, ale są zbilansowane.
W każdym razie, ilekroć przyczepiamy magnesikiem przypominajkę do lodówki, tylekroć doświadczalnie potwierdzamy szczególną teorię względności.
 i długości
i długości
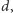 którego
osią symetrii jest „przewodnik”. Z prawa Gaussa wynika, że natężenie
radialnie rozchodzącego się pola elektrycznego, w odległości
którego
osią symetrii jest „przewodnik”. Z prawa Gaussa wynika, że natężenie
radialnie rozchodzącego się pola elektrycznego, w odległości
 od
przewodnika, pomnożone przez powierzchnię boczną walca
od
przewodnika, pomnożone przez powierzchnię boczną walca
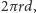 jest
proporcjonalne do ładunku
jest
proporcjonalne do ładunku
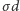 wewnątrz walca. W ten sposób
otrzymujemy
wewnątrz walca. W ten sposób
otrzymujemy