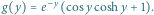Kamerton i struna

Do strojenia instrumentów często wykorzystuje się kamerton widełkowy, wynaleziony w 1711 r. przez Johna Shore’a, lutnistę angielskiego dworu królewskiego. Zaletą tego przyrządu jest to, że wprawiony w ruch emituje dźwięk bardzo „czysty”, tj. zawierający niemal wyłącznie składową wzorcową przyrządu. Zrozumienie, dlaczego tak się dzieje, nie wymaga nadmiernie skomplikowanych rachunków i długich wyjaśnień.
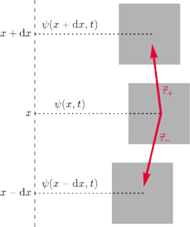
Rys. 1
Równania ruchu
Wyprowadzenie równania ruchu dla struny, czyli równania falowego, można
znaleźć w wielu podręcznikach. Dla porządku przypomnimy tutaj zarys tego
rachunku. Strunę, na którą działa siła naciągu
 możemy podzielić
w myśli na szereg maleńkich kawałków (Rys. 1). Każdy taki kawałek będzie
miał masę
możemy podzielić
w myśli na szereg maleńkich kawałków (Rys. 1). Każdy taki kawałek będzie
miał masę
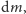 będzie znajdował się w położeniu
będzie znajdował się w położeniu
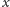 wzdłuż
struny, a jego wychylenie względem pozycji, jaką by miał, gdyby struna
spoczywała, możemy oznaczyć przez
wzdłuż
struny, a jego wychylenie względem pozycji, jaką by miał, gdyby struna
spoczywała, możemy oznaczyć przez
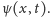 Wówczas II prawo
dynamiki Newtona dla odcinka struny znajdującego się w położeniu
Wówczas II prawo
dynamiki Newtona dla odcinka struny znajdującego się w położeniu
 ma postać:
ma postać:

gdzie
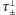 są składowymi sił oddziaływania
są składowymi sił oddziaływania
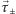 z sąsiednimi
fragmentami struny prostopadłymi do kierunku spoczywającej struny;
wielkość
z sąsiednimi
fragmentami struny prostopadłymi do kierunku spoczywającej struny;
wielkość
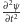 to nic innego jak przyspieszenie w tym kierunku.
Będziemy odtąd zakładać, że wychylenie z położenia równowagi
jest bardzo małe. Ponieważ naciąg struny jest stały, to, przybliżając
to nic innego jak przyspieszenie w tym kierunku.
Będziemy odtąd zakładać, że wychylenie z położenia równowagi
jest bardzo małe. Ponieważ naciąg struny jest stały, to, przybliżając
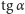 przez
przez
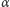 (co jest uzasadnione właśnie dla małych wychyleń),
mamy:
(co jest uzasadnione właśnie dla małych wychyleń),
mamy:

skąd

Dla struny o stałej gęstości liniowej
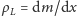 możemy zatem
przepisać równanie ruchu jako
możemy zatem
przepisać równanie ruchu jako
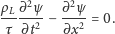 | (1) |
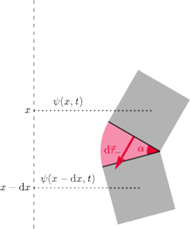
Rys. 2
W przypadku kamertonu źródło siły powodującej jego ruch jest inne. Jeżeli
ramię kamertonu zostanie wygięte, to pojawi się siła sprężystości, która
dla ciał sprężystych spełniających prawo Hooke’a jest proporcjonalna
do odkształcenia ciała. W sytuacji przedstawionej na rysunku 2 wkład
 do siły
do siły
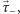 wywieranej na fragment ciała znajdujący się
w położeniu
wywieranej na fragment ciała znajdujący się
w położeniu
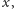 jest proporcjonalny do modułu Younga substancji,
z której wykonane jest ciało, oraz kąta odkształcenia
jest proporcjonalny do modułu Younga substancji,
z której wykonane jest ciało, oraz kąta odkształcenia
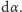 Kąt ten jest
równy kątowi pomiędzy prostymi o nachyleniach
Kąt ten jest
równy kątowi pomiędzy prostymi o nachyleniach
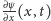 oraz
oraz
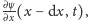 a zatem jest w przybliżeniu równy
a zatem jest w przybliżeniu równy
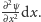 Oznacza
to, że możemy powtórzyć rozumowanie prowadzące do wyznaczenia
równania ruchu dla struny, ale z tą różnicą, że teraz siły
Oznacza
to, że możemy powtórzyć rozumowanie prowadzące do wyznaczenia
równania ruchu dla struny, ale z tą różnicą, że teraz siły
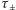 nie mają
stałej wartości, ale są proporcjonalne do
nie mają
stałej wartości, ale są proporcjonalne do
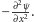 Otrzymujemy
więc:
Otrzymujemy
więc:
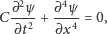 | (2) |
gdzie stała
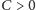 jest odwrotnie proporcjonalna do modułu Younga.
Porównując równania ruchu (1) i (2), stwierdzamy, że w tym drugim
występuje aż czwarta pochodna wychylenia po położeniu. Jak się zaraz
przekonamy, ta drobna z pozoru różnica decyduje o brzmieniu
dźwięku kamertonu.
jest odwrotnie proporcjonalna do modułu Younga.
Porównując równania ruchu (1) i (2), stwierdzamy, że w tym drugim
występuje aż czwarta pochodna wychylenia po położeniu. Jak się zaraz
przekonamy, ta drobna z pozoru różnica decyduje o brzmieniu
dźwięku kamertonu.
Rozwiązanie równań ruchu
Rozwiązania każdego z równań ruchu (1) i (2) można złożyć
z fal stojących, tj. funkcji postaci
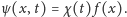 Przyjmiemy,
że funkcja opisująca zależność wychylenia od czasu ma postać
Przyjmiemy,
że funkcja opisująca zależność wychylenia od czasu ma postać
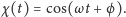 Po podstawieniu do równania (1) otrzymujemy
równanie:
Po podstawieniu do równania (1) otrzymujemy
równanie:

gdzie tzw. związek dyspersyjny ma postać
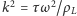 ; rozwiązaniami
tego równania są funkcje
; rozwiązaniami
tego równania są funkcje
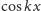 i
i
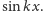 Zakładając, że struna
jest sztywno zamocowana w
Zakładając, że struna
jest sztywno zamocowana w
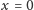 i w
i w
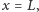 musimy odrzucić
pierwszą klasę rozwiązań, a wśród drugiej klasy dopuścić tylko te, dla
których
musimy odrzucić
pierwszą klasę rozwiązań, a wśród drugiej klasy dopuścić tylko te, dla
których
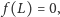 czyli
czyli
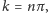 gdzie
gdzie
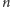 jest liczbą
naturalną. Oznacza to, że widmo częstości takiej struny jest dyskretne
– występuje w nim najniższa częstość
jest liczbą
naturalną. Oznacza to, że widmo częstości takiej struny jest dyskretne
– występuje w nim najniższa częstość
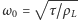 oraz jej
wielokrotności.
oraz jej
wielokrotności.
Podstawiając opisaną wyżej postać rozwiązania do równania (2), otrzymujemy

gdzie związek dyspersyjny ma teraz postać
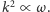 Rozwiązaniem tego równania
jest dowolna kombinacja liniowa funkcji
Rozwiązaniem tego równania
jest dowolna kombinacja liniowa funkcji
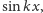
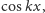
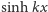 oraz
oraz
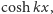 a więc funkcja postaci
a więc funkcja postaci

gdzie stałe
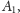
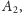
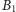 oraz
oraz
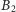 wyznaczymy
z warunków brzegowych. Warunki te dla drgającego pręta o długości
wyznaczymy
z warunków brzegowych. Warunki te dla drgającego pręta o długości
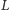 możemy opisać następująco:
możemy opisać następująco:
- 1.
- wychylenie pręta w punkcie
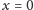 jest zerowe,
jest zerowe,
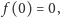
- 2.
- w punkcie
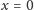 pręt jest pionowy,
pręt jest pionowy,
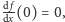
- 3.
- w punkcie
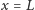 siła sprężystości jest równa zeru,
siła sprężystości jest równa zeru,
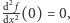
- 4.
- w punkcie
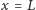 składowa siły sprężystości prostopadła do osi
składowa siły sprężystości prostopadła do osi
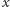 jest równa zeru,
jest równa zeru,
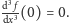
Uwzględnienie tych warunków prowadzi do następującego związku:

a stąd
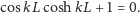 | (3) |
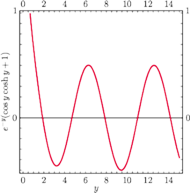
Rozwiązania tego równania możemy wyznaczyć w sposób następujący. Funkcja
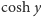 jest bardzo szybko rosnącą funkcją swego argumentu, a więc dla
dostatecznie dużych
jest bardzo szybko rosnącą funkcją swego argumentu, a więc dla
dostatecznie dużych
 miejsca zerowe funkcji
miejsca zerowe funkcji
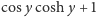 będą
znajdowały się blisko miejsc zerowych funkcji
będą
znajdowały się blisko miejsc zerowych funkcji
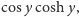 czyli
czyli
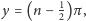 gdzie
gdzie
 jest liczbą naturalną (por. Rys. 3). Lepszą
dokładność możemy uzyskać, zakładając, że
jest liczbą naturalną (por. Rys. 3). Lepszą
dokładność możemy uzyskać, zakładając, że
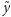 jest pewnym
przybliżeniem szukanego miejsca zerowego i pisząc
jest pewnym
przybliżeniem szukanego miejsca zerowego i pisząc

Rozwijając to w
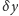 do rzędu kwadratowego, otrzymujemy równanie
do rzędu kwadratowego, otrzymujemy równanie

co pozwala znaleźć dokładniejsze rozwiązanie
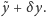 Opisaną
procedurę można powtórzyć, uzyskując rozwiązanie z coraz lepszą
dokładnością. W ten sposób stwierdzamy, że najmniejszymi rozwiązaniami
równania (3) są
Opisaną
procedurę można powtórzyć, uzyskując rozwiązanie z coraz lepszą
dokładnością. W ten sposób stwierdzamy, że najmniejszymi rozwiązaniami
równania (3) są
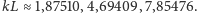 Pamiętając, że
w rozważanym przypadku częstość drgań jest proporcjonalna do kwadratu
liczby falowej
Pamiętając, że
w rozważanym przypadku częstość drgań jest proporcjonalna do kwadratu
liczby falowej
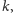 stwierdzamy, że częstości drgań struny i kamertonu
o częstości podstawowej 440 Hz, czyli tonu
stwierdzamy, że częstości drgań struny i kamertonu
o częstości podstawowej 440 Hz, czyli tonu
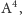 używanego do
strojenia instrumentów, są takie jak w tabeli. Widzimy stąd, że dla kamertonu
druga częstość dozwolonych drgań leży niemal dwie i pół oktawy
powyżej tonu podstawowego, między dźwiękami
używanego do
strojenia instrumentów, są takie jak w tabeli. Widzimy stąd, że dla kamertonu
druga częstość dozwolonych drgań leży niemal dwie i pół oktawy
powyżej tonu podstawowego, między dźwiękami
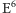 i
i
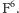 Jest
ona na ogół słabiej słyszalna i łatwa do odróżnienia od częstości
podstawowej, co sprawia, że drgający pręt jest lepszym wzorcem częstości niż
drgająca struna.
Jest
ona na ogół słabiej słyszalna i łatwa do odróżnienia od częstości
podstawowej, co sprawia, że drgający pręt jest lepszym wzorcem częstości niż
drgająca struna.
![-----------------
Cz sto [Hz]
-struna--kamerton-
440 440
880 2763
--1320------7722-](/math/temat/fizyka/mechanika/2012/04/25/Kamerton_i_struna/1x-8f329dac2e32b31e84c81d7d44975e75ff9860f5-dm-33,33,33-FF,FF,FF.gif)
W praktyce stosuje się kamertony zbudowane z dwóch drgających prętów. Takie rozwiązanie pozwala na to, by pręty te drgały w przeciwfazie, a wtedy zamocowanie kamertonu sztywno za uchwyt nie powoduje silnego tłumienia dźwięku.
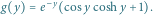
 jest dodatni, funkcja ma te same miejsca zerowe co funkcja we
wzorze (3), jest jednak ograniczona na przedziale
jest dodatni, funkcja ma te same miejsca zerowe co funkcja we
wzorze (3), jest jednak ograniczona na przedziale