O kulach i walcach niestaczających się z równi
Podczas trzynastej edycji Fête de la Science demonstrowaliśmy kule i walce o zaskakującej własności: położone na równi pochyłej nie staczały się z niej, lecz po wykonaniu kilku drgań nieruchomiały. Na fot. 1 pokazano walec i kulę spoczywające na nachylonej powierzchni.

Fig 1 Styropianowa kula i drewniany (pomalowany) walec spoczywające na równi pochyłej.
Za pomocą równi pochyłej i piłki do gry w koszykówkę lub w ping-ponga
łatwo jest sprawdzić, że zazwyczaj już przy bardzo niewielkim kącie
nachylenia
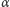 piłka, którą położono na równi, stacza się. Niecodzienny
widok kuli, która pozostaje na równi w spoczynku, budził zdziwienie
widzów. Przygotowane przez nas kule i walce nie staczały się z równi nawet
wówczas, gdy kąt
piłka, którą położono na równi, stacza się. Niecodzienny
widok kuli, która pozostaje na równi w spoczynku, budził zdziwienie
widzów. Przygotowane przez nas kule i walce nie staczały się z równi nawet
wówczas, gdy kąt
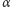 przekraczał
przekraczał
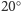 . Widzom odwiedzającym
nasze paryskie „ogrodowe” laboratorium zadawaliśmy pytanie:
. Widzom odwiedzającym
nasze paryskie „ogrodowe” laboratorium zadawaliśmy pytanie:
Jak to możliwe, by kula leżała nieruchomo na pochyłości? Zachęcaliśmy
do stawiania hipotez i do eksperymentowania, w szczególności do obserwacji
zachowania się dziwnych kul i walców przy próbach wprawienia ich
w ruch lub utrzymania w spoczynku, nie tylko na równi pochyłej. Nie
ukrywając faktu, że dziwnie zachowujące się bryły zostały przez nas specjalnie
przygotowane, nie pozwalaliśmy jednak na zajrzenie, co kryją w swych
wnętrzach.
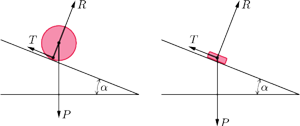
Rys. 1 Siły działające na piłkę (a) i na klocek (b), które położono na równi pochyłej. Piłka nie jest w stanie równowagi.
Piłka na równi
Przeanalizujmy siły działające na piłkę, dzięki którym stacza się ona po równi
pochyłej (Rys. 1). Ziemia przyciąga piłkę siłą grawitacji
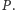 Oddziaływanie
równi na piłkę opisujemy za pomocą siły tarcia
Oddziaływanie
równi na piłkę opisujemy za pomocą siły tarcia
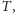 skierowanej wzdłuż
równi w górę, oraz siły reakcji sprężystej
skierowanej wzdłuż
równi w górę, oraz siły reakcji sprężystej
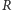 skierowanej prostopadle
do równi, również ku górze. Siły
skierowanej prostopadle
do równi, również ku górze. Siły
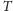 i
i
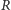 przyłożone są do piłki
w miejscu jej zetknięcia z równią. Czy możliwe jest, by trójka działających
na piłkę sił:
przyłożone są do piłki
w miejscu jej zetknięcia z równią. Czy możliwe jest, by trójka działających
na piłkę sił:
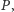
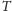 i
i
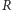 zapewniała jej równowagę? Wynik
prostego doświadczenia, w którym piłkę kładziemy na pochyłości, sugeruje,
że nie ma takiej możliwości. Wiemy jednak, że jeśli zamiast piłki
umieścimy na równi prostopadłościenny klocek, to działające nań siły
zapewniała jej równowagę? Wynik
prostego doświadczenia, w którym piłkę kładziemy na pochyłości, sugeruje,
że nie ma takiej możliwości. Wiemy jednak, że jeśli zamiast piłki
umieścimy na równi prostopadłościenny klocek, to działające nań siły
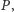
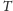 i
i
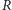 będą się równoważyć. Na przykład zwykła
gumka do wycierania, położona na pochyłej deseczce, pozostaje nieruchoma
nawet przy kącie nachylenia bliskim
będą się równoważyć. Na przykład zwykła
gumka do wycierania, położona na pochyłej deseczce, pozostaje nieruchoma
nawet przy kącie nachylenia bliskim
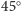 . Gdy gumka jest w równowadze,
siła ciężkości
. Gdy gumka jest w równowadze,
siła ciężkości
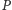 jest zrównoważona wypadkową sił
jest zrównoważona wypadkową sił
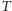 i
i
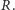 Gdy zwiększyć kąt nachylenia równi, gumka zacznie się
zsuwać, gdyż siła tarcia statycznego nie może przekroczyć pewnej
wartości.
Gdy zwiększyć kąt nachylenia równi, gumka zacznie się
zsuwać, gdyż siła tarcia statycznego nie może przekroczyć pewnej
wartości.
A dlaczego w przypadku piłki jest inaczej? Czemu piłka na równi nie jest w równowadze? Aby wyjaśnić ten fakt, musimy odwołać się do pojęcia momentu siły. Aby ciało rozciągłe, tj. takie, którego rozmiarów nie zaniedbujemy, było w równowadze, spełnione być muszą dwa warunki:
- Suma sił działających na ciało jest równa zeru.
- Suma momentów sił działających na ciało jest równa zeru.
Rys. 2 Jeśli
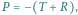 to siły
to siły
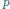 i
i
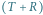 stanowią parę sił, której
moment jest równy
stanowią parę sił, której
moment jest równy
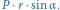
Skoro zwykła piłka nie ma na równi położeń równowagi, to najwidoczniej
nie jest możliwe jednoczesne spełnienie obu warunków. Istotnie, jeśli przyjąć
założenie, że spełniony jest pierwszy z nich, dotyczący sił, to można
wykazać, że nie jest spełniony drugi. Niech
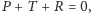 czyli
czyli
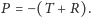 Oznacza to, że siły
Oznacza to, że siły
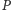 i
i
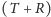 stanowią parę
sił, tzn. układ sił o równoległych kierunkach, równych wartościach
i przeciwnych zwrotach. Jak pokazano na rysunku 2, siły te działają wzdłuż
równoległych prostych, których odległość wynosi
stanowią parę
sił, tzn. układ sił o równoległych kierunkach, równych wartościach
i przeciwnych zwrotach. Jak pokazano na rysunku 2, siły te działają wzdłuż
równoległych prostych, których odległość wynosi
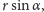 gdzie
gdzie
 to promień kuli. Suma momentów tych sił wynosi
to promień kuli. Suma momentów tych sił wynosi
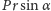 i jest różna od zera (przyjmujemy, że
i jest różna od zera (przyjmujemy, że
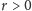 i
i
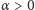 ). Tak więc
na piłkę, którą położono na równi, działają siły, które nie zapewniają stanu
równowagi. W konsekwencji piłka stacza się pod wpływem działającego na nią
momentu sił.
). Tak więc
na piłkę, którą położono na równi, działają siły, które nie zapewniają stanu
równowagi. W konsekwencji piłka stacza się pod wpływem działającego na nią
momentu sił.
Hipotezy
Widzowie uczestniczący w imprezie stawiali rozmaite hipotezy, usiłując wyjaśnić utrzymywanie się kul i walców na pochyłości. Najczęściej sugerowano, że zastosowane zostały magnesy. Wysuwano również inne przypuszczenia: że kula jest naelektryzowana, lub że zawiera specjalny gaz. Sugerowano nawet, że we wnętrzu kuli zamknięto jakieś zwierzę! Wiele z tych hipotez udało się doświadczalnie odrzucić.
Widzowie namawiani przez nas do wykonywania następnych doświadczeń z walcami i kulami spostrzegali, że walec położony nieruchomo na płaskim podłożu wykonuje drgania, tocząc się raz w jedną, raz w drugą stronę. Najbardziej widowiskowe doświadczenie polegało na próbie utrzymania styropianowej kuli na poziomo wyciągniętej dłoni. Eksperymentatorzy odczuwali na własnej skórze, że ta sama kula, która pozostaje nieruchoma na równi, stacza się z poziomo położonej podpory, jaką stanowi dłoń. Najczęściej to właśnie doświadczenie naprowadzało eksperymentatorów na właściwy ślad. Domyślano się wówczas lub stwierdzano: jedna połowa kuli jest cięższa od drugiej.
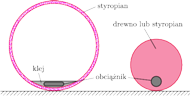
Rys. 3 Budowa kuli i walca z przesuniętymi środkami ciężkości.
Niejednorodne bryły
Najwyższy czas wyjawić, na czym polegał użyty trick sprawiający dziwne
zachowanie się kul i walców: bryły te nie były jednorodne. Pojedynczą kulę
wytwarzano, sklejając dwie półkuliste czasze. Jednakże przed sklejeniem
do wewnętrznej ścianki jednej z nich przymocowywano ołowiany obciążnik.
W sklejonej już kuli obciążnik znajdował się w znacznym oddaleniu od
środka kuli (Rys. 3), a środek ciężkości tak wytworzonej bryły leżał
w pewnej odległości
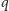 od jej środka geometrycznego (odległość tę
nazywamy mimośrodem). W podobny sposób przesunięto środek
ciężkości walca: kawałek ołowiu umieszczono wewnątrz walca, w pewnej
odległości od jego osi. Obciążniki zawarte w bryłach pozostawały niewidoczne
dla widza.
od jej środka geometrycznego (odległość tę
nazywamy mimośrodem). W podobny sposób przesunięto środek
ciężkości walca: kawałek ołowiu umieszczono wewnątrz walca, w pewnej
odległości od jego osi. Obciążniki zawarte w bryłach pozostawały niewidoczne
dla widza.
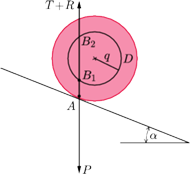
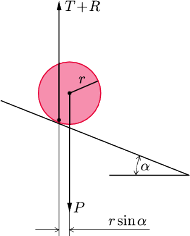
Rys. 4 Siły działające na walec z przesuniętym środkiem ciężkości, położony na równi. Walec jest w stanie równowagi trwałej.
Walec położono na równi pochyłej tak, że jego oś pozostawała pozioma.
Na Rys. 4 pokazano przekrój walca dokonany płaszczyzną równoległą
do podstaw. Widoczny okrąg
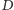 o promieniu
o promieniu
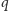 stanowi zbiór
wszystkich punktów, w których może znaleźć się środek ciężkości
walca leżącego w ten sposób na równi.
stanowi zbiór
wszystkich punktów, w których może znaleźć się środek ciężkości
walca leżącego w ten sposób na równi.
Wyjaśnijmy, dlaczego przesunięcie środka ciężkości walca może
zapewnić stabilność walca na równi. Zauważmy, że gdy mimośród jest
odpowiednio duży, to środek ciężkości może znaleźć się dokładnie nad
punktem podparcia
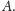 Ściślej: istnieją wówczas dwa punkty okręgu
Ściślej: istnieją wówczas dwa punkty okręgu
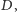 znajdujące się nad punktem
znajdujące się nad punktem
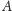 ; oznaczono je
; oznaczono je
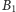 i
i
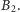 Położenia walca, w których jego środek ciężkości leży
w jednym z tych punktów, są stanami równowagi. Zauważmy, że w obu
stanach równowagi siły
Położenia walca, w których jego środek ciężkości leży
w jednym z tych punktów, są stanami równowagi. Zauważmy, że w obu
stanach równowagi siły
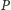 i
i
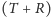 działają wzdłuż tej samej
prostej i w rezultacie suma momentów tych sił jest równa zeru, jeśli tylko siły
te mają jednakową wartość.
działają wzdłuż tej samej
prostej i w rezultacie suma momentów tych sił jest równa zeru, jeśli tylko siły
te mają jednakową wartość.
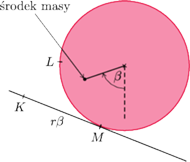
Rys. 5 Określenie kąta
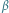 . Gdy
. Gdy
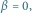 punkty
punkty
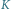 i
i
 pokrywają się,
a środek masy jest w najniższym punkcie okręgu
pokrywają się,
a środek masy jest w najniższym punkcie okręgu
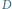 (rys. 4).
(rys. 4).
Szukając ekstremów energii
Energetyczne rozważania zacznijmy jednak od zwykłego jednorodnego walca
(lub jednorodnej kuli). Przyjrzyjmy się, jak zmienia się grawitacyjna energia
potencjalna
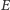 tej bryły toczącej się po równi bez poślizgu. Kąt
tej bryły toczącej się po równi bez poślizgu. Kąt
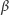 ,
który tworzy z pionem pewna ustalona średnica walca (Rys. 5), przyjmiemy za
parametr opisujący jego położenie. Niech w chwili początkowej
,
który tworzy z pionem pewna ustalona średnica walca (Rys. 5), przyjmiemy za
parametr opisujący jego położenie. Niech w chwili początkowej
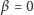 i
i
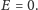 Przy założeniu, że pole grawitacyjne jest jednorodne,
energię potencjalną
Przy założeniu, że pole grawitacyjne jest jednorodne,
energię potencjalną
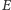 oddziaływania ciała z Ziemią wyrazimy
wzorem
oddziaływania ciała z Ziemią wyrazimy
wzorem
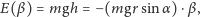 | (1) |
gdzie g jest wartością natężenia ziemskiego pola grawitacyjnego, a wysokość
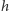 wyznaczamy w odniesieniu do poziomu, na którym znajdował się
środek walca w chwili początkowej. (Uwaga: Kąt
wyznaczamy w odniesieniu do poziomu, na którym znajdował się
środek walca w chwili początkowej. (Uwaga: Kąt
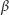 wyrażamy
w radianach, a droga, jaką przebywa środek walca przy obrocie o kąt
wyrażamy
w radianach, a droga, jaką przebywa środek walca przy obrocie o kąt
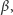 wynosi
wynosi
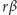 ). Zauważmy, że funkcja
). Zauważmy, że funkcja
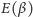 jest
liniowa, co związane jest z faktem, że w rozważanym przypadku środek
masy walca pozostaje w niezmiennej odległości
jest
liniowa, co związane jest z faktem, że w rozważanym przypadku środek
masy walca pozostaje w niezmiennej odległości
 od powierzchni
równi.
od powierzchni
równi.
Zależność
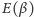 komplikuje się, gdy środek ciężkości walca jest
przesunięty, czyli gdy
komplikuje się, gdy środek ciężkości walca jest
przesunięty, czyli gdy
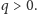 Jeśli założyć, że w chwili początkowej
środek ten znajdował się w najniżej położonym punkcie okręgu
Jeśli założyć, że w chwili początkowej
środek ten znajdował się w najniżej położonym punkcie okręgu
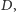 to
czysto geometryczne związki prowadzą do wzoru:
to
czysto geometryczne związki prowadzą do wzoru:

i w konsekwencji
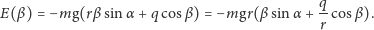 | (2) |
Zauważmy, że oprócz wyrazu występującego we wzorze (1) wzór (2) zawiera
dodatkowy człon proporcjonalny do cosinusa kąta
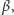 więc okresowo
zmienny.
więc okresowo
zmienny.
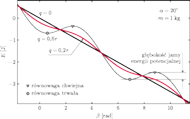
Rys. 6 Zależność grawitacyjnej energii potencjalnej
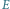 od kąta
od kąta
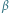 dla walca lub
kuli nieślizgających się po równi.
dla walca lub
kuli nieślizgających się po równi.
Przedstawmy wykres funkcji
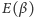 dla konkretnych przykładów
różniących się wartościami ilorazu
dla konkretnych przykładów
różniących się wartościami ilorazu
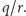 Przyjmijmy:
Przyjmijmy:
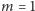 kg,
kg,
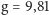 m/s
m/s
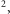
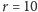 cm,
cm,
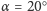 oraz trzy
wartości mimośrodu:
oraz trzy
wartości mimośrodu:
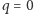 cm (tj. walec z nieprzesuniętym
środkiem ciężkości), 2 cm oraz 6 cm. Na Rys. 6 przedstawiono wykresy
odpowiadające tym przypadkom. Dla pierwszego z nich liniowa funkcja
cm (tj. walec z nieprzesuniętym
środkiem ciężkości), 2 cm oraz 6 cm. Na Rys. 6 przedstawiono wykresy
odpowiadające tym przypadkom. Dla pierwszego z nich liniowa funkcja
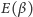 nie ma żadnego ekstremum ani punktu przegięcia, nie ma więc
także położenia równowagi. Gdy
nie ma żadnego ekstremum ani punktu przegięcia, nie ma więc
także położenia równowagi. Gdy
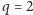 cm,
cm,
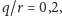 a funkcja
a funkcja
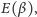 choć nieliniowa, pozostaje monotoniczna i nadal
brak jest położenia równowagi. Jednakże w trzecim rozważanym
przypadku
choć nieliniowa, pozostaje monotoniczna i nadal
brak jest położenia równowagi. Jednakże w trzecim rozważanym
przypadku
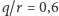 , a funkcja
, a funkcja
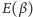 ma minima (oznaczone
na Rys. 6 kółkami) i maksima (oznaczone trójkątami). Wartościom
kąta
ma minima (oznaczone
na Rys. 6 kółkami) i maksima (oznaczone trójkątami). Wartościom
kąta
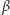 , przy których występują te ekstrema, odpowiadają stany
równowagi.
, przy których występują te ekstrema, odpowiadają stany
równowagi.
Stan równowagi, w którym
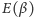 przybiera lokalne minimum, jest
stanem równowagi trwałej. W położeniu tym środek ciężkości walca
znajduje się w punkcie
przybiera lokalne minimum, jest
stanem równowagi trwałej. W położeniu tym środek ciężkości walca
znajduje się w punkcie
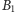 (rys. 4), a fakt ten można sprawdzić
doświadczalnie, zaznaczając położenie środka ciężkości na jednej
z podstaw walca. Trwałość równowagi oznacza, że walec, odchylony
nieznacznie od tego położenia, zmierza do stanu, z którego został wytrącony.
Jeśli jednak wychylenie będzie zbyt duże, to walec podąży ku innemu
położeniu równowagi trwałej. Obszar otaczający minimum energii
potencjalnej nazywamy czasem jamą energii potencjalnej. Im jest ona głębsza,
tym więcej energii trzeba, by wyprowadzić ciało ze stanu równowagi.
W przypadku walca z przesuniętym środkiem ciężkości głębokość (i
szerokość) jamy można w pewnych granicach regulować przez zmianę kąta
(rys. 4), a fakt ten można sprawdzić
doświadczalnie, zaznaczając położenie środka ciężkości na jednej
z podstaw walca. Trwałość równowagi oznacza, że walec, odchylony
nieznacznie od tego położenia, zmierza do stanu, z którego został wytrącony.
Jeśli jednak wychylenie będzie zbyt duże, to walec podąży ku innemu
położeniu równowagi trwałej. Obszar otaczający minimum energii
potencjalnej nazywamy czasem jamą energii potencjalnej. Im jest ona głębsza,
tym więcej energii trzeba, by wyprowadzić ciało ze stanu równowagi.
W przypadku walca z przesuniętym środkiem ciężkości głębokość (i
szerokość) jamy można w pewnych granicach regulować przez zmianę kąta
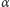 . Na przykład, gdy
. Na przykład, gdy
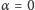 (równia pozioma), głębokość jamy
wynosi
(równia pozioma), głębokość jamy
wynosi
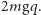 Przy nachylaniu równi, czyli zwiększaniu
Przy nachylaniu równi, czyli zwiększaniu
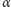 , jama
staje się coraz to płytsza i zanika, gdy punkty
, jama
staje się coraz to płytsza i zanika, gdy punkty
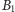 i
i
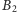 pokrywają
się.
pokrywają
się.
Wartościom kąta
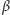 , przy których energia potencjalna przybiera
lokalne maksimum, odpowiada stan równowagi chwiejnej (trójkącik na rys. 6):
walec wytrącony z tego stanu podąża ku innemu stanowi równowagi.
W stanie równowagi chwiejnej środek ciężkości walca znajduje się
w punkcie
, przy których energia potencjalna przybiera
lokalne maksimum, odpowiada stan równowagi chwiejnej (trójkącik na rys. 6):
walec wytrącony z tego stanu podąża ku innemu stanowi równowagi.
W stanie równowagi chwiejnej środek ciężkości walca znajduje się
w punkcie
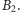 Podczas doświadczeń wykonywano próby utrzymania
walców i kul w stanie równowagi chwiejnej, zadanie to okazywało się jednak
równie trudne, jak utrzymanie na palcu ołówka postawionego na ostrzu
grafitowego pręcika.
Podczas doświadczeń wykonywano próby utrzymania
walców i kul w stanie równowagi chwiejnej, zadanie to okazywało się jednak
równie trudne, jak utrzymanie na palcu ołówka postawionego na ostrzu
grafitowego pręcika.
Stabilność i równowaga
W rozwiązaniach architektonicznych i technicznych niemal nie stosuje się stanów równowagi chwiejnej. Zwykle wymagana jest wysoka stabilność – osiąga się ją, projektując budowle i urządzenia w taki sposób, by przyjmowały stany równowagi trwałej z możliwie głębokimi jamami energii potencjalnej. Jednakże istnieją inne niekonwencjonalne sposoby zapewnienia stabilności. Zanim przedstawimy jeden z nich, przypomnijmy, że stan równowagi to pojęcie ogólniejsze niż stan spoczynku. Ciało jest w równowadze nie tylko, gdy spoczywa, lecz także wtedy, gdy porusza się ruchem jednostajnym prostoliniowym.
Rozpatrzmy lot samolotu wyposażonego w stateczniki, wychylaniem których steruje pilot za pomocą drążka sterowego. Układ sterowania jest tak zaprojektowany, by samolot był samostateczny, tj. by utrzymywał swój prostoliniowy lot także wtedy, gdy pilot puści drążek. Oznacza to, że podczas lotu wykorzystywany jest stan równowagi trwałej.

Samolot F22

Samolot F117
Okazuje się jednak, że obniżając samosterowność samolotu, lub nawet zupełnie z niej rezygnując, można uczynić go bardziej zwrotnym i zmniejszyć opory jego ruchu, a więc także zużycie paliwa. Możliwe jest to jednak jedynie wówczas, gdy bardzo niewielkie odchylenia samolotu od stanu równowagi są dostatecznie szybko korygowane ruchem stateczników i lotek. Szybkość i precyzja reakcji, jakie zapewnić może pilot, okazują się jednak niewystarczające, więc do przeprowadzania (nieustannych) korekcji lotu stosuje się komputer. Umieszczone w samolocie czujniki, m.in. przyspieszeniomierze i żyroskopy, dostarczają komputerowi danych o odchyleniach od stanu równowagi, a program komputerowy zmienia położenie sterów tak, by lot był stabilny. Tak właśnie działa system „fly-by-wire”, dzięki któremu wojskowe samoloty (np. F22) są zdolne do niesamowitych manewrów, a takie jak F117 w ogóle mogą latać. Istotę tego systemu można porównać do czułego układu, który wykrywając odchylenie ołówka od pionu, analizowałby kierunek i kąt wychylenia i sterowałby ruchem ręki tak, by utrzymywać ołówek w stanie bardzo bliskim stanowi równowagi.
Inną skomplikowaną konstrukcją jest Segway, rodzaj elektrycznej hulajnogi na dwóch kołach osadzonych na wspólnej osi. Również i to urządzenie zachowuje równowagę dzięki czujnikom wyznaczającym zmiany położenia środka ciężkości, żyroskopom i komputerowemu sterowaniu.
Przykłady te pokazują, jak ciekawe może być pozornie proste zagadnienie stabilności i jak można niekonwencjonalnie je rozwiązywać. A zadanie określenia położeń równowagi niejednorodnej bryły okazuje się nietrywialnym problemem, choć do jego rozwiązania wystarczają klasyczne prawa statyki.
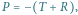 to siły
to siły
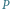 i
i
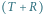 stanowią parę sił, której
moment jest równy
stanowią parę sił, której
moment jest równy
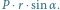
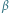 . Gdy
. Gdy
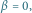 punkty
punkty
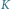 i
i
 pokrywają się,
a środek masy jest w najniższym punkcie okręgu
pokrywają się,
a środek masy jest w najniższym punkcie okręgu
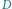 (rys. 4).
(rys. 4).
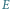 od kąta
od kąta
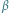 dla walca lub
kuli nieślizgających się po równi.
dla walca lub
kuli nieślizgających się po równi.