Jak to działa?
Trzy ciężkie bąki
Dwa punkty materialne, każdy o masie
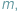 przymocowane są do
przeciwległych punktów nieważkiej obręczy o promieniu
przymocowane są do
przeciwległych punktów nieważkiej obręczy o promieniu
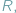 która
toczy się bez tarcia po poziomej płaszczyźnie, pozostając przez cały czas
prostopadła do tej płaszczyzny. Prędkość środka masy układu (punkt
która
toczy się bez tarcia po poziomej płaszczyźnie, pozostając przez cały czas
prostopadła do tej płaszczyzny. Prędkość środka masy układu (punkt
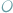 na rysunku 1) wynosi
na rysunku 1) wynosi
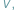 a prędkość kątowa obrotu
względem osi przechodzącej przez
a prędkość kątowa obrotu
względem osi przechodzącej przez
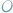 jest równa
jest równa
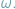 Jaka jest
energia tego układu?
Jaka jest
energia tego układu?
Rys. 1 Dwa punkty na obręczy toczące się po poziomej płaszczyźnie.
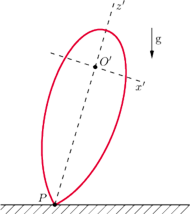
Rys. 2 Bąk ciężki.
Środek masy układu znajduje się stale na tej samej wysokości, zatem energia
potencjalna siły ciężkości jest stała. Ruch każdego z punktów jest
złożeniem ruchu postępowego z prędkością
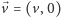 oraz ruchu po
okręgu z prędkością
oraz ruchu po
okręgu z prędkością
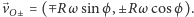 Zatem wypadkowe
prędkości punktów
Zatem wypadkowe
prędkości punktów
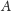 i
i
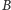 wynoszą:
wynoszą:

Łączna energia kinetyczna tych punktów wynosi więc:
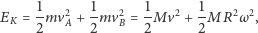 | (*) |
gdzie wprowadziliśmy oznaczenie
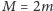 dla całkowitej masy układu.
Widać, że prawa strona ( * ) jest sumą dwóch składników o jasnych
znaczeniach: pierwszy związany jest z ruchem środka masy, drugi niesie
informację o obrocie względem osi stałej względem ciała i przechodzącej przez
środek masy. Współczynnik mnożący
dla całkowitej masy układu.
Widać, że prawa strona ( * ) jest sumą dwóch składników o jasnych
znaczeniach: pierwszy związany jest z ruchem środka masy, drugi niesie
informację o obrocie względem osi stałej względem ciała i przechodzącej przez
środek masy. Współczynnik mnożący
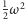 w drugim wyrazie nosi
nazwę momentu bezwładności względem tej osi i jest równy sumie iloczynów
mas punktów układu i kwadratów odległości tych punktów od osi obrotu.
Gdyby ciało toczyło się bez poślizgu, punkt
w drugim wyrazie nosi
nazwę momentu bezwładności względem tej osi i jest równy sumie iloczynów
mas punktów układu i kwadratów odległości tych punktów od osi obrotu.
Gdyby ciało toczyło się bez poślizgu, punkt
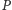 styku obręczy
z podłożem spoczywałby, gdyż mielibyśmy
styku obręczy
z podłożem spoczywałby, gdyż mielibyśmy
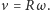 Moglibyśmy
wówczas rozważać obrót ciała względem chwilowej osi przechodzącej przez
ten punkt styczności, a energia kinetyczna wyrażałaby się wzorem
Moglibyśmy
wówczas rozważać obrót ciała względem chwilowej osi przechodzącej przez
ten punkt styczności, a energia kinetyczna wyrażałaby się wzorem
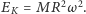 Nietrudno sprawdzić, że moment bezwładności
obliczony względem tej osi wynosi
Nietrudno sprawdzić, że moment bezwładności
obliczony względem tej osi wynosi
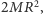 co po pomnożeniu przez
co po pomnożeniu przez
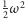 znowu daje energię kinetyczną obrotu.
znowu daje energię kinetyczną obrotu.
W powyższym zadaniu oś obrotu pozostawała stała względem obracającego
się ciała, ale w ogólnym przypadku tak wcale być nie musi. Okazuje się, że dla
dowolnego ciała obracającego się wględem ustalonego punktu istnieją trzy
prostopadłe osie
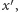
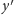 i
i
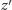 przechodzące przez punkt
obrotu, takie że momenty bezwładności obliczone względem tych osi wynoszą
przechodzące przez punkt
obrotu, takie że momenty bezwładności obliczone względem tych osi wynoszą
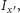
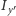 oraz
oraz
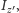 a energia kinetyczna obrotu jest
równa
a energia kinetyczna obrotu jest
równa

gdzie
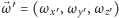 jest wektorem skierowanym wzdłuż chwilowej
osi obrotu, współczynniki
jest wektorem skierowanym wzdłuż chwilowej
osi obrotu, współczynniki
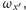
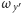 i
i
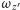 to jego składowe
w układzie współrzędnych wyznaczonym przez osie
to jego składowe
w układzie współrzędnych wyznaczonym przez osie
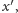
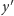 i
i
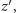 natomiast długość wektora
natomiast długość wektora
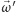 jest równa prędkości
kątowej.
jest równa prędkości
kątowej.
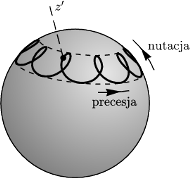
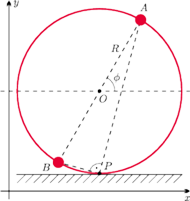
Rys. 3 Ruch symetrycznego bąka ciężkiego.
Szczególnym przypadkiem takich ruchów obrotowych jest ruch – w ziemskim
polu grawitacyjnym – ciała, którego jeden punkt został przegubowo
unieruchomiony w ustalonym punkcie
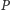 (Rys. 2). Ciało takie nazywamy
bąkiem ciężkim. Gdy bąk ciężki jest symetryczny, tj. ma symetrię obrotową
względem osi
(Rys. 2). Ciało takie nazywamy
bąkiem ciężkim. Gdy bąk ciężki jest symetryczny, tj. ma symetrię obrotową
względem osi
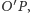 łączącej środek masy
łączącej środek masy
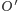 z punktem
nieruchomym
z punktem
nieruchomym
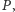 analiza zasady zachowania energii prowadzi
do wniosku, że ruch osi symetrii
analiza zasady zachowania energii prowadzi
do wniosku, że ruch osi symetrii
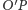 jest złożeniem ruchu
precesyjnego i nutacyjnego, którego przykład przedstawia rysunek 3.
Jakościową słuszność takiego rozwiązania potwierdzi każdy, kto –
niekoniecznie w dzieciństwie – bawił się zabawką również zwaną
bąkiem.
jest złożeniem ruchu
precesyjnego i nutacyjnego, którego przykład przedstawia rysunek 3.
Jakościową słuszność takiego rozwiązania potwierdzi każdy, kto –
niekoniecznie w dzieciństwie – bawił się zabawką również zwaną
bąkiem.
A co, jeśli bąk nie jest symetryczny? Okazuje się, że ogólne rozwiązanie równań ruchu bąka ciężkiego (z dowolnymi warunkami początkowym) nie daje się uzyskać poza trzema przypadkami. Są nimi:
- opisany wyżej bąk Lagrange’a: momenty bezwładności
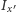 i
i
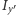 są równe, a środek masy
są równe, a środek masy
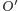 leży
na osi odpowiadającej momentowi bezwładności
leży
na osi odpowiadającej momentowi bezwładności
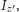
- bąk
Eulera:
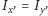 oraz unieruchomiony punkt jest środkiem
masy ciała,
oraz unieruchomiony punkt jest środkiem
masy ciała,
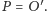
- bąk Kowalewskiej:
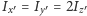 oraz środek masy ciała
leży w płaszczyźnie
oraz środek masy ciała
leży w płaszczyźnie