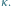Możliwość zmierzenia czegokolwiek wymaga spełnienia dwóch warunków. Potrzebny jest pomysł i – nazwijmy to jakoś – możliwości techniczne. Żeby wykonać prosty pomiar długości, czasu, temperatury itp., wystarczy odpowiednio wyskalowany przyrząd, bo pomysł jest oczywisty.

Co należy zrobić, żeby sprawdzić, czy jabłko rzeczywiście spada ruchem jednostajnie przyspieszonym?

Należy odwołać się do definicji przyspieszenia. Wielkość ta jest po prostu miarą tempa zmiany prędkości. Jeżeli ciało porusza się ruchem jednostajnie przyspieszonym, to w każdym kolejnym przedziale czasu jego prędkość zmienia się o tyle samo. Inaczej mówiąc, wykres zależności prędkości od czasu powinien być linią prostą. Współczynnik kierunkowy tej prostej, czyli stosunek przyrostu prędkości do czasu, w którym ten przyrost następuje, jest, oczywiście, miarą przyspieszenia

Sprawa nie wydaje się trudna. Należy po prostu wykonać taki wykres. Przy okazji wyznaczymy wówczas przyspieszenie ziemskie g. Jest jednak pewien problem. Żeby wyznaczyć prędkość spadającego jabłka, należy zmierzyć, jak wysoko znajduje się ono w kolejnych chwilach. A to jest bardzo trudne bez odpowiedniego wyposażenia technicznego.

Dlatego, jeżeli już wykonuje się doświadczenia, które sprawdzają, czy ciała rzeczywiście spadają ruchem jednostajnie przyspieszonym, to zazwyczaj nie są to pomiary bezpośrednie. Używa się równi pochyłych albo wahadła.

Tymczasem konieczne wyposażenie techniczne jest coraz bardziej dostępne. Potrzebna jest kamera cyfrowa, statyw i…pomysł, jak te możliwości techniczne wykorzystać. Kręcąc film ze spadającym jabłkiem w roli głównej, rejestrujemy jego pozycję co 1/25 sekundy (wartość typowa dla kamer cyfrowych na polskim rynku). Należy film przegrać do komputera, rozbić na pojedyncze klatki i, wykorzystując dowolny program do obróbki zdjęć, zmierzyć tę pozycję na każdej klatce. Jeżeli zdjęcia będą miały w tle coś, co pozwoli na wyznaczenie odległości w pionie, to analizując je, będziemy mogli nie tylko sprawdzić, czy jabłko spada ruchem jednostajnie przyspieszonym, ale również to przyspieszenie wyznaczyć. Montaż takiej sekwencji ujęć przedstawiony jest na zdjęciu (pokazana jest co piąta klatka, czyli pozycja jabłka co dwie dziesiąte sekundy).

Zdjęcie przedstawia rzut ukośny, ale to przecież też jest spadek swobodny w pewnym układzie inercjalnym (jakim?). Jabłko powinno poruszać się ruchem jednostajnym w kierunku poziomym i ruchem z jednostajnym przyspieszeniem w kierunku pionowym. Rzut został wykonany na tle ściany wyłożonej regularnymi płytami, co pozwala określić skalę. Doświadczalnie zostało sprawdzone, że rzut ukośny ma kilka przewag nad spadkiem swobodnym. Po pierwsze, nie trzeba umieszczać pomocników na dwóch poziomach (przy okazji zaświadczam, że jabłku nie stała się żadna krzywda, zostało ono później komisyjnie zjedzone przez ekipę filmową). Po drugie, możliwy do sfilmowania lot jest dwa razy dłuższy (dlaczego to jest istotne?).

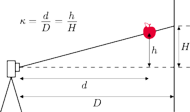
Rys. 1 Wyznaczenie współczynnika

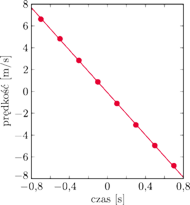
Rys. 2 Wykres zależności średniej pionowej składowej prędkości jabłka od czasu dla przedziałów między kolejnymi pozycjami jabłka ze zdjęcia na poprzedniej stronie. Jako dodatni został przyjęty zwrot w górę.

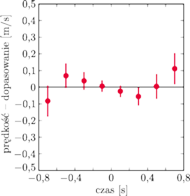
Rys. 3 Wykres różnic między wartością prędkości a przedstawioną na górnym panelu dopasowaną prostą.

Choć ściana jest regularna, to środkowe płyty są na zdjęciu minimalnie wyższe niż te u dołu i góry. Obiektyw aparatu tylko do pewnego stopnia spełnia wzór soczewkowy. Każdy obiektyw powoduje mniejsze lub większe zniekształcenie, takie jak widoczne przy zdjęciach obiektywami typu rybie oko. Jest ono tym mniejsze, im większy jest stosunek ogniskowej do rozmiaru powstającego w aparacie obrazu. Dlatego zdjęcia należy robić z jak największej odległości, wykorzystując zoom optyczny. Oprócz tego dobrze jest zadbać o dobre oświetlenie (tu oświetlenie mogłoby być lepsze – zbyt długie otwarcie migawki powoduje rozmycie jabłka na dole zdjęcia). W pierwszym podejściu pominiemy jednak te problemy. Okaże się, że dokładność pomiarów jest zbyt mała, żeby się nimi przejmować.

Pozostaje jednak jeden efekt, który musimy skorygować. Chodzi o błąd paralaksy spowodowany tym, że płaszczyzna rzutu jest w pewnej odległości od ściany, którą wykorzystujemy jako miarkę. Problem ten możemy rozwiązać za pomocą twierdzenia Talesa. Odległość w pikselach od linii poziomej dzielącej (niewykadrowane) zdjęcie na pół (na tej wysokości znajdowała się ustawiono poziomo kamera) należy pomnożyć przez 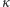stosunek odległości: kamera – płaszczyzna ruchu jabłka i kamera – ściana (Rys. 1). W tym konkretnym przypadku odległość została zmierzona krokami i stosunek 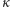wyniósł

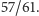
Na rysunku 2 przedstawiona jest zależność pionowej składowej prędkości jabłka od czasu. Ponieważ do wyznaczenia prędkości (średniej) potrzebna jest różnica położeń, to punktów na wykresie jest o jeden mniej niż jabłek na zdjęciu. Punkty układają się na dopasowanej do nich prostej, więc nie mamy podstaw, żeby twierdzić, że nie jest to ruch z jednostajnym przyspieszeniem.

Niepewności pomiaru są zbyt małe (przyjęto niepewność od jednego piksela dla położenia centralnego do trzech pikseli dla położeń skrajnych), żeby były widoczne. Dlatego poniżej przedstawiony jest wykres różnic między zmierzonym położeniem a dopasowaniem, za pomocą którego można wizualnie ocenić stopień zgodności punktów z prostą (Rys. 3).

Parametrem dopasowania jest przyspieszenie (współczynnik kierunkowy dopasowywanej prostej):

Dodatkowo pomiar jest obarczony błędem względnym rzędu 1% w związku z niepewnością wyznaczenia stosunku odległości

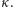
Wygląda na to, że Newton znał się na jabłkach.

Autor dziękuje za pomoc w przeprowadzeniu sesji zdjęciowej
Piotrowi TRACZYKOWI i Pawłowi ZYCHOWI.