Achilles, żeby dogonił żółwia, musi najpierw znaleźć się w miejscu, w którym teraz znajduje się żółw, ale przez ten czas żółw trochę się przesunie itd. Strzała, żeby dolecieć do tarczy, musi najpierw przebyć połowę odległości, następnie połowę połowy itd. Zenon twierdził, że w takim razie ani Achilles nie powinien dogonić żółwia, ani strzała dolecieć do tarczy. W konsekwencji pojęcie ruchu jest wewnętrznie sprzeczne. Twierdzili tak eleaci, którzy uważali, że jest tylko byt, a niebytu nie ma. W takim razie nie ma ruchu, bo ruch musiałby powodować przejście do czegoś, czego nie ma. A jak czegoś nie ma, to nie ma i nie można do tego przejść.

Pozostali filozofowie greccy aż tak drastycznie do ruchu nie podchodzili, ale ani oni, ani ich następcy (aż do Newtona) nie potrafili sobie z pojęciem prędkości poradzić.

Należy jednak pamiętać, że dla starożytnych ruch był przedmiotem rozważań filozoficznych, a obecnie jest to przedmiot badań fizyki. Cele tych nauk są różne, więc nie można bezpośrednio porównywać poglądów starożytnych i współczesnych, bo to tak, jakby przeciwstawiać sobie twierdzenia: „jabłko jest okrągłe” i „jabłko jest smaczne”.

Obecnie wiemy, że choć strzała rzeczywiście musi przebyć ten nieskończony ciąg odcinków

to jeśli pokonuje każdy z nich w czasie proporcjonalnym do jego długości, to dotrze do celu w skończonym czasie

a więc ze stałą prędkością 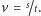Wydaje się, że nie ma w tym nic odkrywczego, ale to tylko dlatego, że się do tego przyzwyczailiśmy. Tak naprawdę „prędkość jest stosunkiem drogi do czasu” tylko dla ruchu jednostajnego (lub dla prędkości średniej). Ogólnie, prędkość (chwilowa) jest to „granica ilorazu wyrazów dwóch ciągów”. Jednego opisującego przebywaną drogę w coraz mniejszych odcinkach czasu i drugiego opisującego właśnie te coraz mniejsze odcinki czasu. Aby robić to w sposób dający poprawne wyniki należy użyć rachunku różniczkowego.