Drobiazgi

Co ma wspólnego cykl (6, 5, 4) z językiem polskim?

Każdej liczbie rzeczywistej możemy przypisać nieskończony ciąg cyfr jej rozwinięcia dziesiętnego. Jak wiadomo, jeżeli ciąg od pewnego miejsca się zapętla, to mamy do czynienia z liczbą wymierną. Inaczej rzecz ujmując, liczby wymierne mają okresowe rozwinięcie dziesiętne. Przyjmujemy tutaj, że tzw. rozwinięcie skończone jest rozwinięciem okresowym - od pewnego miejsca na każdej pozycji występuje wyłącznie cyfra 0.

My będziemy rozważać ciągi liczbowe. Możemy przyjąć jakąś konkretną metodę produkcji kolejnych wyrazów ciągu, na przykład

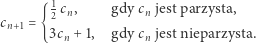1c , gdy c jest parzysta, cn+1 = { 2 n n 3cn + 1, gdy cn jest nieparzysta.

Jednak stwierdzenie, czy dla dowolnej początkowej liczby 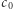$c 0$ ten ciąg zawsze się zapętli, jest nie lada wyzwaniem. Tego dotyczy problem Collatza - ale to nie on jest bohaterem tego tekstu.

W 1972 roku zespół z Artificial Intelligence Laboratory, Massachusetts Institute of Technology, opracował raport Hakmem - złożony z prawie dwustu algorytmicznych ciekawostek (miszmasz algebry, kombinatoryki, teorii liczb, teorii grup $|...$ ). Pozycja 134. wspomnianego raportu także dotyczy ciągów liczbowych i ich zapętlania. Przyjmijmy następującą zasadę:

Każdy element ciągu (oprócz pierwszego) określa, ile liter jest potrzebnych do zapisania słownie (w języku angielskim) poprzedniego elementu ciągu.

Zacznijmy na przykład od liczby 14. Słowo fourteen ma osiem liter, więc drugi element ciągu to 8. Słowo eight ma pięć liter, kolejny element ciągu to 5. Słowo five ma cztery litery - podobnie jak four. Zatem

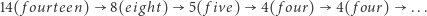14( f ourteen) 8(eight) 5( five) 4( four) 4( four) ...

i tym sposobem otrzymujemy ciąg 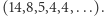$(14,8,5,4,4, ...).$ Co ciekawe, niezależnie od tego, od jakiej liczby zaczniemy, dany ciąg zawsze (i szybko) zapętli się na liczbie 4.

Czy już się domyślasz, Czytelniku, jak brzmi odpowiedź na tytułowe pytanie?