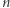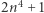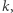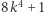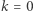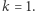Piramida kwadratowych liczb
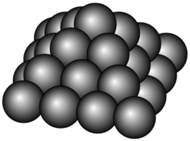
Piramidy w starożytnym Egipcie budowano na kształt ostrosłupa prawidłowego o podstawie kwadratu. Jak pokazują źródła historyczne, starożytni Egipcjanie potrafili obliczyć objętość takiego ostrosłupa. Jednak ich dobrze rozwinięta, jak na tamte czasy, matematyka, miała głównie zastosowanie praktyczne i raczej nikt nie formułował pytań, które miałyby na celu jedynie matematyczną rozrywkę. Jednym z matematyków, który szczególnie interesował się rozrywkowymi zastosowaniami królowej nauk, był Édouard Lucas, autor między innymi słynnej gry zwanej Wieżą Hanoi. W niniejszym artykule zwrócimy uwagę na sformułowany przez Lucasa problem z gatunku tych raczej mało praktycznych. Jak zobaczymy, ma on pewien związek z piramidami.
Wyobraźmy sobie piramidę o podstawie kwadratu utworzoną z jednakowych kul. W 1875 roku Édouard Lucas rzucił wyzwanie czytelnikom pewnego czasopisma matematycznego (nie była to Delta - przyp. red.), formułując
Problem ten można zapisać w formie równania diofantycznego
 |
gdzie 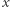 jest liczbą kul armatnich w rzędzie tworzącym bok kwadratu będącego podstawą piramidy, a
jest liczbą kul armatnich w rzędzie tworzącym bok kwadratu będącego podstawą piramidy, a 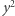 sumą wszystkich kul składających się na piramidę. Posługując się wzorem na sumę kwadratów pierwszych kolejnych liczb naturalnych, powyższe równanie możemy również zapisać w sposób równoważny jako
sumą wszystkich kul składających się na piramidę. Posługując się wzorem na sumę kwadratów pierwszych kolejnych liczb naturalnych, powyższe równanie możemy również zapisać w sposób równoważny jako
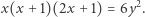 |
Lucas postawił poniższą hipotezę.
Hipoteza. Jedynymi parami liczb naturalnych spełniającymi równanie
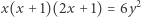 |
są 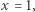
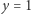 oraz
oraz 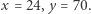
Okazała się ona prawdziwa, jednak początkowe próby jej udowodnienia były nieskuteczne. Sam autor również opublikował rzekomy dowód, jednak zawierał on lukę, której przez długi czas nikomu nie udało się uzupełnić. Dopiero w 1918 roku George Neville Watson przedstawił pierwsze kompletne uzasadnienie hipotezy Lucasa. Było ono jednak obszerne i wykorzystywało zaawansowane narzędzia. Dopiero później pojawiły się mniej wyrafinowane dowody. W dalszej części tego artykułu przedstawimy szkic jednego z nich, który można uznać za stosunkowo prosty, gdyż opiera się na elementarnej teorii liczb.
Niech para 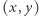 będzie rozwiązaniem powyższego równania. W pierwszej części dowodu załóżmy, że
będzie rozwiązaniem powyższego równania. W pierwszej części dowodu załóżmy, że  jest parzyste. Pomocne będą poniższe dwa lematy, których techniczne dowody przedstawimy w szkicowej postaci.
jest parzyste. Pomocne będą poniższe dwa lematy, których techniczne dowody przedstawimy w szkicowej postaci.
Lemat 1. Nie istnieje trójkąt prostokątny o bokach całkowitych, którego pole jest liczbą kwadratową.
Szkic dowodu. Przypuśćmy, że  jest najmniejszą liczbą naturalną, dla której istnieją
jest najmniejszą liczbą naturalną, dla której istnieją 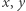 spełniające
spełniające 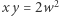 oraz
oraz 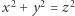 dla pewnego
dla pewnego 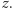 Zgodnie ze znaną charakterystyką rozwiązań drugiego z tych równań możemy przyjąć
Zgodnie ze znaną charakterystyką rozwiązań drugiego z tych równań możemy przyjąć  (
(  względnie pierwsze) i wówczas
względnie pierwsze) i wówczas 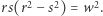 Ze względnej pierwszości
Ze względnej pierwszości  i
i  wynika
wynika 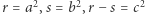 i
i 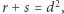 skąd
skąd 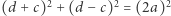 oraz
oraz 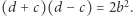 Mamy jednak
Mamy jednak 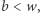 co przeczy definicji
co przeczy definicji  i kończy dowód.
i kończy dowód.
Szkic dowodu. Niech 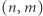 będzie rozwiązaniem równania
będzie rozwiązaniem równania 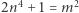 o możliwie najmniejszej wartości
o możliwie najmniejszej wartości 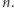 Wówczas
Wówczas 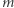 jest nieparzyste i możemy przekształcić równanie do postaci
jest nieparzyste i możemy przekształcić równanie do postaci 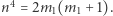 Jeśli
Jeśli 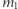 jest nieparzyste, to
jest nieparzyste, to 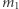 i
i  są względnie pierwsze, a zatem dla pewnych
są względnie pierwsze, a zatem dla pewnych 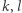 mamy
mamy 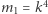 i
i 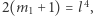 skąd rozważając modulo 8, szybko otrzymujemy sprzeczność. Zatem
skąd rozważając modulo 8, szybko otrzymujemy sprzeczność. Zatem 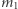 jest parzyste i podobnie wnioskujemy
jest parzyste i podobnie wnioskujemy 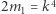 i
i 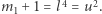 W tej sytuacji
W tej sytuacji 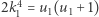 (gdzie
(gdzie 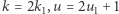 ). Z
). Z 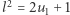 wnioskujemy (modulo 4) parzystość
wnioskujemy (modulo 4) parzystość 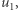 skąd
skąd  i
i 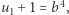 czyli
czyli 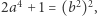 co daje nam sprzeczność z minimalnością
co daje nam sprzeczność z minimalnością 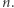
Szkic dowodu. Przypuśćmy, że 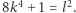 Wówczas
Wówczas 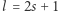 i
i 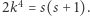 Jeśli
Jeśli  jest parzyste, to
jest parzyste, to 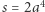 i
i 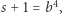 a zatem
a zatem 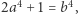 skąd i z lematu 2 mamy
skąd i z lematu 2 mamy 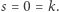 Jeśli
Jeśli  jest nieparzyste, to
jest nieparzyste, to 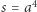 i
i 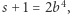 czyli
czyli 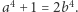 Wnioskujemy stąd (modulo 4), że liczby
Wnioskujemy stąd (modulo 4), że liczby 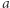 i
i 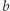 są nieparzyste, ponadto podnosząc ostatnią równość do kwadratu i przekształcając, dostaniemy
są nieparzyste, ponadto podnosząc ostatnią równość do kwadratu i przekształcając, dostaniemy  Ze względnej pierwszości
Ze względnej pierwszości 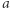 i
i  mamy
mamy 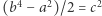 i
i 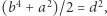 a zatem
a zatem 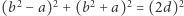 i
i 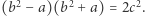 Zgodnie z lematem 1 oznacza to, że
Zgodnie z lematem 1 oznacza to, że 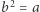 i w konsekwencji
i w konsekwencji 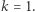
Powróćmy do hipotezy Lucasa. Skoro  jest parzyste, to
jest parzyste, to 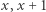 i
i 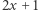 są parami względnie pierwsze. Stąd
są parami względnie pierwsze. Stąd 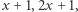 jako liczby nieparzyste, są albo kwadratami, albo potrójnymi kwadratami. Zatem
jako liczby nieparzyste, są albo kwadratami, albo potrójnymi kwadratami. Zatem 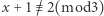 oraz
oraz  a stąd
a stąd 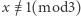 oraz
oraz  co daje również, że
co daje również, że 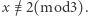 Ostatecznie
Ostatecznie 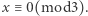 Wobec tego liczby
Wobec tego liczby 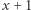 i
i 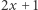 są kwadratami (gdyby były potrójnymi kwadratami, nie byłyby względnie pierwsze z
są kwadratami (gdyby były potrójnymi kwadratami, nie byłyby względnie pierwsze z 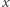 ). Wtedy dla pewnych liczb naturalnych
). Wtedy dla pewnych liczb naturalnych 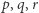 parami względnie pierwszych możemy zapisać
parami względnie pierwszych możemy zapisać
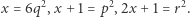 |
Ponadto  a skoro
a skoro 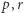 są nieparzyste, to
są nieparzyste, to 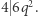 Wtedy
Wtedy 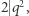 czyli
czyli 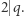
Ze względnej pierwszości 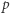 i
i  wynika względna pierwszość liczb całkowitych
wynika względna pierwszość liczb całkowitych 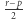 i
i 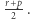
Niech  będzie liczbą całkowitą taką, że
będzie liczbą całkowitą taką, że 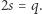 Wtedy
Wtedy  Skoro
Skoro 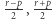 są względnie pierwsze, to otrzymujemy dwie możliwości.
są względnie pierwsze, to otrzymujemy dwie możliwości.
- 1)
- Jedna z liczb
 jest postaci
jest postaci 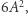 a druga
a druga 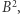 gdzie
gdzie 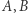 są nieujemne całkowite. Wtedy
są nieujemne całkowite. Wtedy 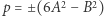 i
i 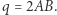 Skoro jednak
Skoro jednak 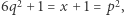 to
to 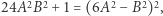 czyli
czyli 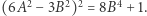 Korzystając z lematu 3, otrzymujemy
Korzystając z lematu 3, otrzymujemy  Stąd
Stąd 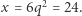
- 2)
- Jedna z liczb
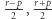 jest postaci
jest postaci 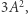 a druga
a druga 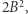 gdzie
gdzie 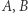 są nieujemne całkowite. Wtedy
są nieujemne całkowite. Wtedy 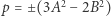 i
i  Wobec równości
Wobec równości 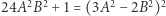 otrzymujemy, że
otrzymujemy, że 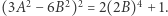 Następnie z lematu 2 wnioskujemy, że nie istnieje liczba całkowita dodatnia
Następnie z lematu 2 wnioskujemy, że nie istnieje liczba całkowita dodatnia 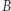 spełniająca powyższe założenia. Stąd równanie
spełniająca powyższe założenia. Stąd równanie 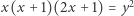 nie ma rozwiązań w tym przypadku.
nie ma rozwiązań w tym przypadku.
Wykazaliśmy więc, że gdy  jest parzyste, to problem Lucasa ma tylko jedno rozwiązanie:
jest parzyste, to problem Lucasa ma tylko jedno rozwiązanie: 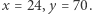
Pozostaje nam sytuacja, kiedy to 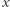 jest nieparzyste. Najpierw odwołamy się do dość znanego w teorii liczb równania Pella, a właściwie do jego szczególnego przypadku, to znaczy równania
jest nieparzyste. Najpierw odwołamy się do dość znanego w teorii liczb równania Pella, a właściwie do jego szczególnego przypadku, to znaczy równania 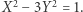 Wiemy, że jego wszystkie rozwiązania to ciąg liczb
Wiemy, że jego wszystkie rozwiązania to ciąg liczb
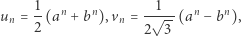 |
gdzie 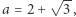
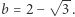
Do przeprowadzenia drugiej części dowodu potrzebny będzie jeszcze jeden lemat, którego dowód również pominiemy. Bazuje on na pewnej obserwacji dotyczącej rozwiązań równania 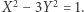
Dowód wspomnianego wyżej lematu również nie jest skomplikowany, jednak opiera się na kilku innych obserwacjach dotyczących własności rekurencyjnych ciągu rozwiązań równania 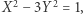 których treści tutaj pominiemy, gdyż same w sobie nie są one dla nas szczególnie interesujące.
których treści tutaj pominiemy, gdyż same w sobie nie są one dla nas szczególnie interesujące.
Skoro 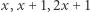 są parami względnie pierwsze, to
są parami względnie pierwsze, to  jest kwadratem albo potrójnym kwadratem i
jest kwadratem albo potrójnym kwadratem i 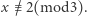 Wówczas
Wówczas 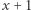 (parzyste) jest odpowiednio albo kwadratem pomnożonym przez 6, albo podwójnym kwadratem. Zatem
(parzyste) jest odpowiednio albo kwadratem pomnożonym przez 6, albo podwójnym kwadratem. Zatem 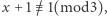 a stąd już łatwo wywnioskować, że
a stąd już łatwo wywnioskować, że 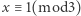 i
i  Wtedy istnieją takie liczby naturalne
Wtedy istnieją takie liczby naturalne 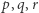 parami względnie pierwsze, że
parami względnie pierwsze, że
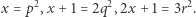 |
Następnie otrzymujemy, że  Ponadto
Ponadto
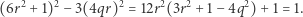 |
Równanie to przyjęło postać szczególnego równania Pella, przy czym 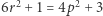 odpowiada wyrazom ciągu
odpowiada wyrazom ciągu 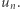 Korzystając z lematu 3, otrzymujemy
Korzystając z lematu 3, otrzymujemy 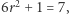 co daje nam
co daje nam 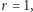 a wtedy
a wtedy 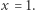 Uzyskaliśmy drugie rozwiązanie problemu Lucasa. Tym samym zakończyliśmy dowód jego hipotezy.
Uzyskaliśmy drugie rozwiązanie problemu Lucasa. Tym samym zakończyliśmy dowód jego hipotezy.
Rozważając powyższe piramidy, można zadać sobie również pytanie, kiedy suma kul jest liczbą trójkątną, czyli poszukać rozwiązań równania diofantycznego
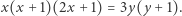 |
Na to również są znane wyniki. Aby dostarczyć sobie matematycznej rozrywki, czemu by nie zadać innego warunku dla liczby będącej sumą kul? Jeśli tylko mamy do czynienia z pewnym ciągiem liczb, którego jawny wzór jest nam znany, to cała zabawa sprowadza się do rozwiązania odpowiedniego równania diofantycznego. Tym samym zachęcam Cię, drogi Czytelniku, do sformułowania podobnego problemu.