Ziemiolubne liczby i ulotne reszty
Człowiek twardo stąpa po ziemi, a z nim pojęcia, które stworzył. Na przykład liczby są tylko tym, do czego człowiekowi służą: porządkowe, kardynalne i inne. W skończonych zastosowaniach są to liczby naturalne 1, 2, 3, ... i ich uogólnienia: liczby całkowite, wymierne, rzeczywiste i zespolone. Słowo skończone w poprzednim zdaniu odnosi się wyłącznie do opisywanego atrybutu liczonego obiektu: a to jego rangi, a to mocy, a to fizycznych rozmiarów. W matematyce teoretycznej liczb praktycznie zawsze potrzebujemy nieskończenie wiele!

Wróćmy zatem na ubitą przez tysiąclecia glebę teorii liczb. Jak udowodnić najprościej, że równanie
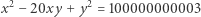 |
nie ma rozwiązań w liczbach całkowitych 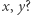 Można na przykład zauważyć, że odpowiednia kongruencja mod 4 nie ma rozwiązań. Wynika to stąd, że kwadrat liczby całkowitej zawsze przystaje do 0 lub 1 modulo 4, a zatem lewa jej strona przystaje do 0,1,2 modulo 4, a prawa do 3.
Można na przykład zauważyć, że odpowiednia kongruencja mod 4 nie ma rozwiązań. Wynika to stąd, że kwadrat liczby całkowitej zawsze przystaje do 0 lub 1 modulo 4, a zatem lewa jej strona przystaje do 0,1,2 modulo 4, a prawa do 3.
Nie zawsze jest tak łatwo i o tym właśnie jest ten artykuł. Rozważmy mianowicie równanie
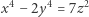 |
(1) |
i zapytajmy o jego rozwiązania w liczbach całkowitych nieujemnych  Jeśli
Jeśli 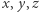 jest takim rozwiązaniem oraz
jest takim rozwiązaniem oraz 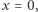 to
to  a więc również
a więc również  Załóżmy teraz nie wprost, że istnieje rozwiązanie, w którym
Załóżmy teraz nie wprost, że istnieje rozwiązanie, w którym 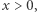 i rozważajmy dalej jedno z rozwiązań, w których
i rozważajmy dalej jedno z rozwiązań, w których 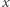 przyjmuje wartość dodatnią najmniejszą z możliwych. Udowodnimy przede wszystkim, że wówczas
przyjmuje wartość dodatnią najmniejszą z możliwych. Udowodnimy przede wszystkim, że wówczas
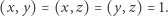 |
(2) |
( 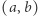 oznacza największy wspólny dzielnik liczb całkowitych
oznacza największy wspólny dzielnik liczb całkowitych 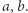 ) Niech
) Niech 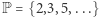 oznacza dalej zbiór wszystkich liczb pierwszych. Załóżmy, że istnieje takie
oznacza dalej zbiór wszystkich liczb pierwszych. Załóżmy, że istnieje takie 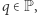 że
że 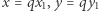 dla pewnych
dla pewnych 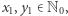 przy czym
przy czym  Po podstawieniu tych wartości do równania (1) otrzymujemy
Po podstawieniu tych wartości do równania (1) otrzymujemy
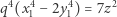 |
i stąd dostajemy, że 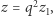 gdzie
gdzie  (również dla
(również dla 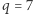 ). Liczby
). Liczby 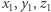 spełniają zatem równanie (1), przy czym
spełniają zatem równanie (1), przy czym 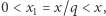 sprzeczność z wyborem
sprzeczność z wyborem  Udowodniliśmy więc, że
Udowodniliśmy więc, że 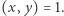 Analogicznie wykazujemy, że
Analogicznie wykazujemy, że 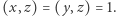 Z (1) i (2) wynika, że wszystkie liczby
Z (1) i (2) wynika, że wszystkie liczby 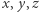 są nieparzyste. Rzeczywiście, gdyby
są nieparzyste. Rzeczywiście, gdyby  była parzysta, to z (1) wynika, że również
była parzysta, to z (1) wynika, że również  byłaby parzysta, skąd
byłaby parzysta, skąd 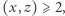 sprzeczność z (2). Podobnie
sprzeczność z (2). Podobnie  jest nieparzysta. Gdyby
jest nieparzysta. Gdyby 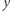 była parzysta to mielibyśmy kongruencję
była parzysta to mielibyśmy kongruencję
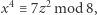 |
ale to nie jest możliwe, gdyż kwadrat liczby nieparzystej przystaje do 1 mod 8:
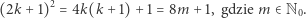 |
Zatem  jest również nieparzysta. Wykażemy teraz, że
jest również nieparzysta. Wykażemy teraz, że
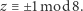 |
(3) |
Jeśli 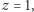 to (3) oczywiście zachodzi. Gdy
to (3) oczywiście zachodzi. Gdy 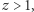 rozpatrujemy dowolny dzielnik pierwszy
rozpatrujemy dowolny dzielnik pierwszy  liczby
liczby 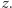 Mamy
Mamy 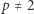 oraz z równania (1) wynika kongruencja
oraz z równania (1) wynika kongruencja
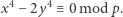 |
Ponieważ 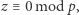 więc
więc 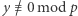 na mocy (2). Niech
na mocy (2). Niech 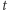 będzie takie, że
będzie takie, że 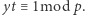 Wówczas
Wówczas
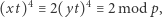 |
czyli kongruencja 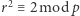 ma rozwiązanie, np.
ma rozwiązanie, np. 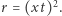 Teraz trzeba przywołać słynne twierdzenie z teorii reszt kwadratowych. Jako pierwszy udowodnił je Gauss:
Teraz trzeba przywołać słynne twierdzenie z teorii reszt kwadratowych. Jako pierwszy udowodnił je Gauss:
Twierdzenie. Jeśli 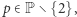 to kongruencja
to kongruencja 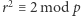 ma rozwiązanie wtedy i tylko wtedy, gdy
ma rozwiązanie wtedy i tylko wtedy, gdy 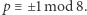
Podsumujmy: liczba  jest iloczynem swoich czynników pierwszych
jest iloczynem swoich czynników pierwszych 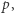 a zatem (3) zachodzi. Skoro
a zatem (3) zachodzi. Skoro 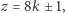 więc
więc 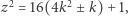 czyli
czyli 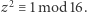 Z podobnych powodów
Z podobnych powodów  Zatem lewa
Zatem lewa  i prawa
i prawa 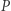 strona równania (1) spełniają następujące kongruencje:
strona równania (1) spełniają następujące kongruencje:
 |
co daje upragnioną sprzeczność.
Jedynym rozwiązaniem równania (1) w liczbach całkowitych jest więc trójka 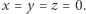 W finale dowodu rozstrzygającą rolę odegrały rozważania modulo 16. Nie jest jednak prawdą, że kongruencja
W finale dowodu rozstrzygającą rolę odegrały rozważania modulo 16. Nie jest jednak prawdą, że kongruencja
 |
nie ma rozwiązań w liczbach nieparzystych. Wystarczy wziąć 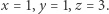

Nie jest to przypadek. W pozostałej części artykułu pokażemy, że dla każdej liczby 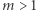 istnieją liczby całkowite
istnieją liczby całkowite 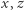 spełniające kongruencję
spełniające kongruencję
 |
(4) |
Oznacza to, że strategia dowodu, że równanie (1) nie ma całkowitych rozwiązań poza 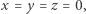 polegająca na szukaniu liczby
polegająca na szukaniu liczby 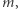 dla której kongruencja
dla której kongruencja
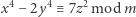 |
nie ma rozwiązań  spełniających
spełniających 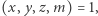 nie może się powieść.
nie może się powieść.
Z twierdzenia chińskiego o resztach wynika, że można się ograniczyć do przypadku, gdy 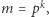 gdzie
gdzie  Najpierw rozpatrzmy przypadek
Najpierw rozpatrzmy przypadek 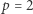 i połóżmy
i połóżmy 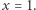 Wykażemy, że dla każdego
Wykażemy, że dla każdego 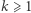 istnieje
istnieje 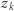 spełniające kongruencję
spełniające kongruencję
 |
(5) |
Dla 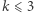 bierzemy
bierzemy 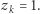 Załóżmy teraz, że dla pewnego
Załóżmy teraz, że dla pewnego 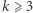 istnieją takie
istnieją takie 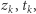 że
że 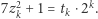 Wykażemy, że istnieją takie
Wykażemy, że istnieją takie 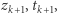 że
że  Niech
Niech 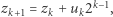 gdzie
gdzie 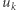 dobierzemy za chwilę. Modulo
dobierzemy za chwilę. Modulo 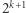 mamy
mamy

Liczbę  dobieramy tak, aby prawa strona powyższego wzoru była podzielna przez
dobieramy tak, aby prawa strona powyższego wzoru była podzielna przez 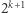 :
:
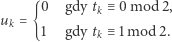 |
To działa, gdyż  jest nieparzyste.
jest nieparzyste.
Zajmiemy się teraz kongruencją (4) dla 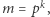 gdzie
gdzie 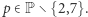 Dla
Dla 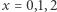 otrzymujemy odpowiednio kongruencje
otrzymujemy odpowiednio kongruencje
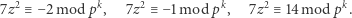 |
Niech  spełnia warunek
spełnia warunek 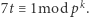 Powyższe kongruencje są równoważne następującym:
Powyższe kongruencje są równoważne następującym:
 |
(6) |
Ponieważ zredukowana grupa reszt modulo 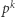 jest cykliczna oraz
jest cykliczna oraz
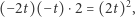 |
więc przynajmniej jedna z kongruencji (6) ma rozwiązanie  (jedna lub wszystkie). W istocie chodzi tu o to, że iloczyn niereszt kwadratowych jest resztą kwadratową itd. Czytelnikowi pozostawiamy przypadek
(jedna lub wszystkie). W istocie chodzi tu o to, że iloczyn niereszt kwadratowych jest resztą kwadratową itd. Czytelnikowi pozostawiamy przypadek 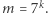
Podobną własność jak równanie (1) mają równania
![3 3 3 3x + 4y + 5z = 0 [E. Selmer, 1951],](/math/temat/matematyka/teoria_liczb/2020/05/31/ziemiolubne-liczby-i-ulotne-reszty/1x-6debaaee854394341ad302b2be6018ebcd34eb7c-dm-33,33,33-FF,FF,FF.gif) |
![x4− 17y4 = 2z2 [H. Reichardt, 1942].](/math/temat/matematyka/teoria_liczb/2020/05/31/ziemiolubne-liczby-i-ulotne-reszty/1x-6ad1d0031f3d1750dd8808270a1849f70c66920c-dm-33,33,33-FF,FF,FF.gif) |
Były to w zasadzie pierwsze przykłady nietrywialnych równań diofantycznych, które nie spełniają zasady lokalno-globalnej, czyli nie mają nietrywialnych rozwiązań wymiernych, mimo że odpowiednie kongruencje mod 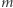 mają nietrywialne rozwiązania dla każdej liczby
mają nietrywialne rozwiązania dla każdej liczby 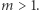 Nie ma takich równań stopnia
Nie ma takich równań stopnia 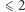 dowolnej liczby zmiennych, gdyż zachodzi następujące słynne twierdzenie Hassego-Minkowskiego:
dowolnej liczby zmiennych, gdyż zachodzi następujące słynne twierdzenie Hassego-Minkowskiego:
Twierdzenie. Niech 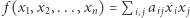 będzie formą kwadratową nieokreśloną o współczynnikach całkowitych. Jeśli dla każdego
będzie formą kwadratową nieokreśloną o współczynnikach całkowitych. Jeśli dla każdego 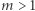 kongruencja
kongruencja 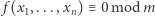 ma rozwiązanie
ma rozwiązanie 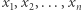 spełniające
spełniające 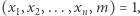 to istnieją
to istnieją  że
że 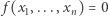 oraz
oraz 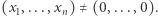
Nierozwiązalność kongruencji 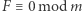 dla liczby
dla liczby 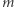 odpowiednio dobranej do badanego równania diofantycznego
odpowiednio dobranej do badanego równania diofantycznego 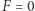 jest ewidentną przeszkodą dla jego rozwiązalności w liczbach całkowitych. Przykłady takie, jak Selmera, Reichardta, równanie (1) i wiele, wiele innych dotykają trudnej rzeczywistości: czasem przeszkody na drodze do rozwiązalności są bardziej subtelne i głębiej ukryte. I tak np. równania reprodukowane w tym tekście dają nietrywialne elementy grupy Szafarewicza-Tate'a odpowiednich krzywych eliptycznych. Kryje się za tym wszystkim matematyka nowoczesna i abstrakcyjna, ale jednocześnie bardzo, bardzo konkretna - nasz przykład równania (1) ilustruje oczywiście tylko ten drugi aspekt. Ma to być jednak wystarczającą zachętą dla Czytelnika Zainteresowanego teorią liczb, aby pogłębić swoje studia tego fascynującego działu matematyki:)
jest ewidentną przeszkodą dla jego rozwiązalności w liczbach całkowitych. Przykłady takie, jak Selmera, Reichardta, równanie (1) i wiele, wiele innych dotykają trudnej rzeczywistości: czasem przeszkody na drodze do rozwiązalności są bardziej subtelne i głębiej ukryte. I tak np. równania reprodukowane w tym tekście dają nietrywialne elementy grupy Szafarewicza-Tate'a odpowiednich krzywych eliptycznych. Kryje się za tym wszystkim matematyka nowoczesna i abstrakcyjna, ale jednocześnie bardzo, bardzo konkretna - nasz przykład równania (1) ilustruje oczywiście tylko ten drugi aspekt. Ma to być jednak wystarczającą zachętą dla Czytelnika Zainteresowanego teorią liczb, aby pogłębić swoje studia tego fascynującego działu matematyki:)