Trójkąt harmoniczny – bliźniak trójkąta Pascala
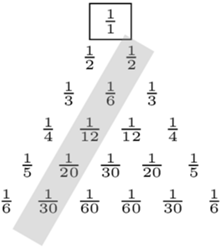
Trójkąt Pascala zna praktycznie każdy. Widoczny poniżej z lewej strony trójkąt ma tę własność, że każda liczba jest sumą dwóch liczb stojących bezpośrednio nad nią (z wyłączeniem wierzchołka trójkąta oraz jego prawego i lewego boku, gdzie znajdują się jedynki). Z kolei w trójkącie po prawej stronie każda liczba jest sumą dwóch liczb stojących bezpośrednio pod nią. Na jego prawym oraz lewym boku znajdują się odwrotności kolejnych liczb naturalnych - liczby harmoniczne. Taki obiekt nazywa się trójkątem harmonicznym. Konstrukcję obu trójkątów można oczywiście kontynuować w nieskończoność...

Spoglądając na oba trójkąty, można dostrzec pewne zależności zachodzące między nimi. Na przykład liczby w ostatnim widocznym wierszu trójkąta Pascala są dzielnikami mianowników liczb ostatniego wiersza trójkąta harmonicznego. W tym tekście przyjrzymy się dokładniej trójkątowi harmonicznemu.
Niech 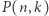 oznacza
oznacza 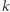 -ty wyraz
-ty wyraz 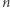 -tego wiersza w trójkącie Pascala (wiersze oraz wyrazy numerujemy od 0), a
-tego wiersza w trójkącie Pascala (wiersze oraz wyrazy numerujemy od 0), a 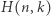 oznacza
oznacza 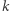 -ty wyraz
-ty wyraz  -tego wiersza w trójkącie harmonicznym (numerujemy od 1).
-tego wiersza w trójkącie harmonicznym (numerujemy od 1).
Wprost z opisu konstrukcji trójkątów otrzymujemy następujące relacje:

Wartość  to
to 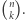 Nasuwa się więc pytanie o ogólny wzór dowolnego wyrazu trójkąta harmonicznego.
Nasuwa się więc pytanie o ogólny wzór dowolnego wyrazu trójkąta harmonicznego.
Z tego wynika następująca zależność między wartościami obu trójkątów
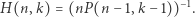 |
Dowód. Rozumowanie przebiega indukcyjnie względem 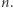 Sprawdzenie przypadków
Sprawdzenie przypadków 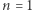 oraz
oraz 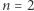 zostawiamy Czytelnikowi i przechodzimy do założenia indukcyjnego. Załóżmy zatem, że wzór jest prawdziwy dla pewnego
zostawiamy Czytelnikowi i przechodzimy do założenia indukcyjnego. Załóżmy zatem, że wzór jest prawdziwy dla pewnego 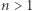 oraz
oraz 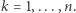 Wykażemy, że wzór zachodzi dla
Wykażemy, że wzór zachodzi dla 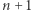 oraz wszystkich
oraz wszystkich 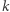 od
od 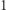 do
do 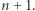 Rozumowanie ponownie przebiega indukcyjnie, przy czym przypadek
Rozumowanie ponownie przebiega indukcyjnie, przy czym przypadek 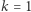 jest oczywisty. Załóżmy więc, że tożsamość jest prawdziwa dla pewnego
jest oczywisty. Załóżmy więc, że tożsamość jest prawdziwa dla pewnego 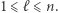 Wtedy korzystając z faktu i po stosownych przekształceniach:
Wtedy korzystając z faktu i po stosownych przekształceniach:

Rozumowanie to kończy oba postępowania indukcyjne.
Korzystając z tego wzoru, otrzymujemy na przykład, że piąty wiersz trójkąta harmonicznego to
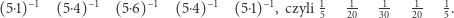 |
W trójkącie Pascala można znaleźć wiele ciekawych zależności na sumy wybranych elementów. Jedną z najbardziej zaskakujących jest związek
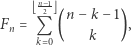 |
gdzie 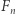 jest
jest  -tą liczbą Fibonacciego. Mniej znaną jest natomiast relacja
-tą liczbą Fibonacciego. Mniej znaną jest natomiast relacja
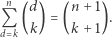 |
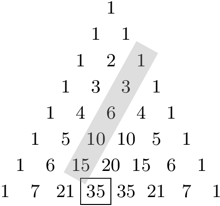
Przez skos trójkąta zawsze będziemy oznaczać zbiór liczb stojących na odcinku równoległym do boku trójkąta, o początku w jego boku.
Oznacza to, że jeżeli weźmiemy liczby znajdujące się na skosie trójkąta (dowolnym skosie, ale równoległym do jego boku; patrz rysunek), to suma liczb na tym skosie będzie równa liczbie pod nim (tej, która nie leży na przedłużeniu skosu), na przykład

Istnieje analogiczna relacja dla trójkąta harmonicznego, którą sformułujemy w kolejnym twierdzeniu.
Powyższa równość oznacza w szczególności, że każda liczba harmoniczna jest nieskończoną sumą liczb na skosie trójkąta, na przykład 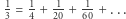 Co więcej, analogiczna równość jest prawdziwa dla każdej liczby w tym trójkącie.
Co więcej, analogiczna równość jest prawdziwa dla każdej liczby w tym trójkącie.
Dowód. Dla ustalonego 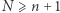 możemy, korzystając z rekurencyjnej definicji elementów trójkąta harmonicznego, napisać
możemy, korzystając z rekurencyjnej definicji elementów trójkąta harmonicznego, napisać

Teza twierdzenia wynika teraz z oczywistego faktu, że granica 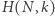 przy
przy 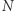 dążącym do nieskończoności wynosi 0.
dążącym do nieskończoności wynosi 0.
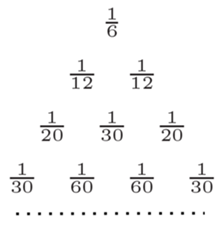
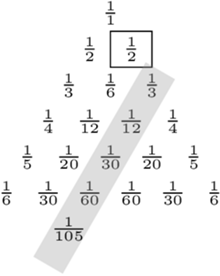
Spójrzmy teraz na ułamki znajdujące się wewnątrz trójkąta harmonicznego, czyli te, które nie znajdują się na jego bokach (patrz rysunek obok).
Jaka jest suma wszystkich takich wyrazów? Odpowiedź jest zaskakująco prosta.


Dowód. Z twierdzenia 3 wynika, że 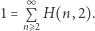 Korzystając raz jeszcze (i wielokrotnie) z twierdzenia 3, otrzymujemy
Korzystając raz jeszcze (i wielokrotnie) z twierdzenia 3, otrzymujemy

Postępujemy tak analogicznie aż do równości
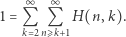 |
Zamieniając kolejność sumowania (we wzorze powyżej - sumujemy po skosach), otrzymujemy tezę.
Twierdzenie 4 można uogólnić!
Dowód powyższego twierdzenia w oparciu o przedstawione powyżej wyniki pozostawiamy Czytelnikowi Dociekliwemu.
Twierdzenia 4 i 5 mają następującą interpretację: każdy element trójkąta harmonicznego jest sumą wszystkich elementów w trójkącie, które leżą poniżej i pomiędzy dwoma skosami zawierającymi daną liczbę. Można zapytać o to, czy istnieje jakaś analogia twierdzenia 6 dla trójkąta Pascala. Czytelnik może sprawdzić, że każdy element trójkąta Pascala pomniejszony o 1 jest sumą wszystkich elementów tego trójkąta, które leżą powyżej i pomiędzy dwoma skosami zawierającymi daną liczbę. Życzymy owocnych poszukiwań kolejnych zależności.
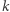
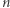
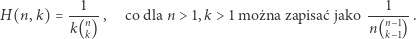

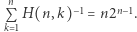
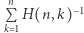 można zapisać w postaci
można zapisać w postaci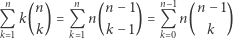
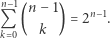
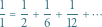
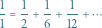
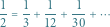
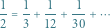
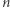
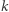
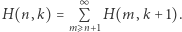
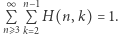
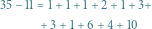
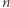
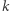
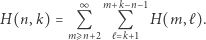
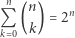
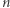 -elementowego.
-elementowego.