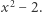Trudniej, a łatwiej
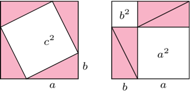
Są twierdzenia łatwe i trudne do udowodnienia. Zazwyczaj im mocniejsze sformułowanie, obejmujące więcej przypadków, tym trudniej się je dowodzi. Tak jest na przykład z twierdzeniem cosinusów i twierdzeniem Pitagorasa, które jest jego szczególnym przypadkiem. Łatwiej jest udowodnić twierdzenie Pitagorasa; można to zrobić nawet w sposób zrozumiały dla przedszkolaka (zobacz rysunek obok). Do dowodu twierdzenia cosinusów trzeba przynajmniej wiedzieć, co to cosinus, w szczególności kąta rozwartego.
Jest jednak metoda dowodzenia, w której dowody mocniejszych twierdzeń bywają łatwiejsze niż ich sformułowań mniej ogólnych. To indukcja matematyczna.
Weźmy taki przykład. Postarajmy się udowodnić, że suma sześcianów początkowych  liczb naturalnych jest pełnym kwadratem, czyli kwadratem pewnej liczby naturalnej. Spróbujmy dowodu indukcyjnego. Sprawdzamy bazę dla
liczb naturalnych jest pełnym kwadratem, czyli kwadratem pewnej liczby naturalnej. Spróbujmy dowodu indukcyjnego. Sprawdzamy bazę dla 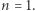 Działa:
Działa: 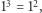 czyli suma pojedynczego sześcianu jedynki jest kwadratem jedności (dla
czyli suma pojedynczego sześcianu jedynki jest kwadratem jedności (dla 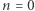 zresztą też działa!). Załóżmy teraz, że
zresztą też działa!). Załóżmy teraz, że 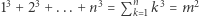 dla pewnego naturalnego
dla pewnego naturalnego 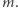 Mamy wykazać, że
Mamy wykazać, że
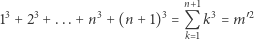 |
dla pewnej liczby naturalnej 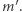 Stosujemy założenie indukcyjne:
Stosujemy założenie indukcyjne:
 |
i klops! Tego się nie da już doprowadzić do niczego sensownego. Dowód się zacina.
Wystarczy jednak wzmocnić nieco tezę: nie tylko twierdzić, że jest to pełny kwadrat jakiejś liczby, ale ją bezpośrednio wskazać: tą liczbą jest suma początkowych  liczb naturalnych, czyli
liczb naturalnych, czyli  Nasze mocniejsze twierdzenie mówi, że
Nasze mocniejsze twierdzenie mówi, że 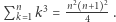 Teraz krok indukcyjny działa bez zarzutu: Zakładamy, że
Teraz krok indukcyjny działa bez zarzutu: Zakładamy, że 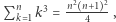 i dowodzimy, że
i dowodzimy, że  Elementarne rachunki nas w tym upewniają:
Elementarne rachunki nas w tym upewniają:
 |
Co się stało? Po prostu z mocniejszych założeń wyciągamy więcej wniosków. A że założenie jest częściowo tezą? Tym lepiej! Nic dziwnego, że przy indukcji matematycznej krok indukcyjny dowodzi się prościej, gdy założenie jest silniejsze. Zobaczmy jeszcze jeden przykład.
Spróbujmy wykazać, że dla każdego  wartość
wartość 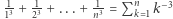 jest mniejsza od
jest mniejsza od 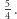 Gdybyśmy użyli zwykłej indukcji, to co prawda baza indukcji by była prawdziwa, bo
Gdybyśmy użyli zwykłej indukcji, to co prawda baza indukcji by była prawdziwa, bo 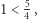 ale z krokiem indukcyjnym byłoby już trudniej. Załóżmy bowiem, że
ale z krokiem indukcyjnym byłoby już trudniej. Załóżmy bowiem, że
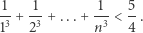 |
Mamy wykazać, że
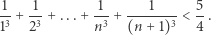 |
I widać gołym okiem, że założenie indukcyjne do niczego nam się nie przyda. Co z tego, że suma odwrotności sześcianów aż do 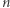 włącznie jest mniejsza od
włącznie jest mniejsza od 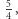 skoro nie wiemy, o ile jest mniejsza i czy
skoro nie wiemy, o ile jest mniejsza i czy 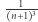 tam się jeszcze zmieści?
tam się jeszcze zmieści?
Widać, że dużego pola manewru nie mamy. Po prostu założenie indukcyjne było zbyt słabe. Spróbujmy zatem wzmocnić tezę, twierdząc, że nie tylko ta suma jest mniejsza od 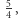 ale wręcz od
ale wręcz od 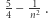
Co? Że to wcale nie jest prawda? Faktycznie: już dla 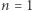 ta nierówność nie zachodzi. Dla
ta nierówność nie zachodzi. Dla 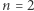 również, nawet dla
również, nawet dla 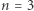 okazuje się, że
okazuje się, że  przekracza wartość
przekracza wartość 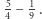 Ale dla
Ale dla 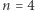 już jest OK:
już jest OK:
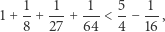 |
co można sprawdzić za pomocą kalkulatora, albo nawet bez.
Teraz już jest łatwo. Stawiamy hipotezę indukcyjną, że dla 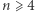 zachodzi
zachodzi
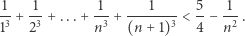 |
Baza już jest udowodniona. Pozostaje krok indukcyjny. Zakładamy zatem, że
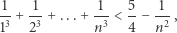 |
i wykażemy, że
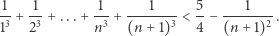 |
To już jest proste.
Mamy bowiem na mocy założenia indukcyjnego
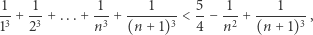 |
a wykazanie, że prawa strona tej nierówności jest mniejsza od  to już jest elementarna algebra. Wystarczy obie strony przemnożyć przez niewątpliwie dodatnią wartość
to już jest elementarna algebra. Wystarczy obie strony przemnożyć przez niewątpliwie dodatnią wartość 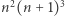 i zredukować powstałą nierówność do równoważnej oczywistej
i zredukować powstałą nierówność do równoważnej oczywistej 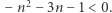
W ten sposób udowodniliśmy, że nierówność ta zachodzi dla wszystkich 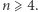 Przypadki, gdy
Przypadki, gdy  możemy sprawdzić ręcznie - ostatecznie dla
możemy sprawdzić ręcznie - ostatecznie dla 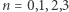 liczb po prostu wyjściowa nierówność jest spełniona z prawą stroną równą
liczb po prostu wyjściowa nierówność jest spełniona z prawą stroną równą 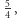 a dla
a dla 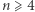 nawet mocniejsza, z odjętym składnikiem
nawet mocniejsza, z odjętym składnikiem 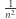 po prawej stronie.
po prawej stronie.
Przy okazji można zadać narzucające się pytanie: czy 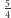 jest najlepszym przybliżeniem sumy nieskończonego szeregu odwrotności sześcianów? Wiemy, że ciąg jego sum częściowych rośnie wraz z
jest najlepszym przybliżeniem sumy nieskończonego szeregu odwrotności sześcianów? Wiemy, że ciąg jego sum częściowych rośnie wraz z  i ma ograniczenie górne, więc z twierdzenia Weierstrassa wynika, że ma granicę. Czy jest nią
i ma ograniczenie górne, więc z twierdzenia Weierstrassa wynika, że ma granicę. Czy jest nią  Nie. Można lepiej oszacować tę wartość z góry. Próbowało tego wielu matematyków; pierwszym chyba był Euler, któremu nie udało się rozwiązać zagadki do końca. Podał co prawda związek tej granicy, z której istnienia zdawał sobie zresztą sprawę, z innymi sumami parzystych potęg odwrotności liczb naturalnych. Choć udało mu się wyznaczyć dokładne postacie granic szeregów z drugimi i czwartymi potęgami,
Nie. Można lepiej oszacować tę wartość z góry. Próbowało tego wielu matematyków; pierwszym chyba był Euler, któremu nie udało się rozwiązać zagadki do końca. Podał co prawda związek tej granicy, z której istnienia zdawał sobie zresztą sprawę, z innymi sumami parzystych potęg odwrotności liczb naturalnych. Choć udało mu się wyznaczyć dokładne postacie granic szeregów z drugimi i czwartymi potęgami, 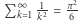 oraz
oraz 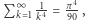 to na trzeciej potędze się zaciął.
to na trzeciej potędze się zaciął.
Nic dziwnego. Mimo z górą dwustuletnich starań matematyków do dziś nie znamy wyrażenia definiującego tę wartość; nie wiemy, czy w ogóle takie wyrażenie istnieje. Znamy ponad bilion (czyli 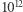 ) cyfr rozwinięcia dziesiętnego tej liczby, którego początek to 1,2020569031595942853997381615. Wiemy, że jest to liczba niewymierna, choć zostało to udowodnione dopiero w roku 1978 przez francuskiego matematyka Rogera Apéry'ego i od jego nazwiska stała ta jest od tej pory nazywana stałą Apéry'ego. Pojawia się ona zresztą w naturalny sposób przy rozwiązywaniu pewnych zagadnień fizycznych, jak wyznaczanie współczynnika żyromagnetycznego (ilorazu momentu magnetycznego przez moment obrotowy), a także informatycznych przy analizie minimalnych losowych drzew rozpinających graf.
) cyfr rozwinięcia dziesiętnego tej liczby, którego początek to 1,2020569031595942853997381615. Wiemy, że jest to liczba niewymierna, choć zostało to udowodnione dopiero w roku 1978 przez francuskiego matematyka Rogera Apéry'ego i od jego nazwiska stała ta jest od tej pory nazywana stałą Apéry'ego. Pojawia się ona zresztą w naturalny sposób przy rozwiązywaniu pewnych zagadnień fizycznych, jak wyznaczanie współczynnika żyromagnetycznego (ilorazu momentu magnetycznego przez moment obrotowy), a także informatycznych przy analizie minimalnych losowych drzew rozpinających graf.
Nie wiemy do tej pory, czy liczba ta jest algebraiczna i czy kiedykolwiek poznamy jej symboliczną postać odnoszącą się na przykład do znanych stałych, takich jak  czy
czy  Zagadkowa sprawa.
Zagadkowa sprawa.
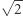 jest algebraiczny, ponieważ jest pierwiastkiem wielomianu
jest algebraiczny, ponieważ jest pierwiastkiem wielomianu