Mały Gauss
Już rok po śmierci Gaussa (w 1856 r.) ukazała się książka wspomnieniowa jego wieloletniego przyjaciela Wolfganga Sartoriusa von Waltershausena Zum Gauss Gedächtniss. Trzeba o niej wiedzieć co najmniej z dwóch powodów. Stąd pochodzi najsłynniejszy aforyzm z matematyką w roli głównej. Jako teoretyk liczb przytoczę go z przyjemnością w pełnej postaci: Matematyka jest królową nauk, a arytmetyka królową matematyki.
Drugi powód to tytułowy kleiner Gauss - tak w obszarze niemieckojęzycznym nazywa się czasem pochodzący z głębokiej starożytności wzór na sumę pierwszych  liczb naturalnych. Nazwa nawiązuje bezpośrednio do najpopularniejszej anegdoty, w której występuje matematyk, podanej właśnie w tej książce. Nie wypada tej anegdoty tu przypominać, gdyż każdy Czytelnik Delty na pewno ją zna. Zastanówmy się tylko, co bardziej kierowało Büttnerem, nauczycielem młodziutkiego Gaussa - chęć poskromienia urwisów, czy też nadzieja wyłowienia perły?
liczb naturalnych. Nazwa nawiązuje bezpośrednio do najpopularniejszej anegdoty, w której występuje matematyk, podanej właśnie w tej książce. Nie wypada tej anegdoty tu przypominać, gdyż każdy Czytelnik Delty na pewno ją zna. Zastanówmy się tylko, co bardziej kierowało Büttnerem, nauczycielem młodziutkiego Gaussa - chęć poskromienia urwisów, czy też nadzieja wyłowienia perły?
To, że ten dylemat każdego ambitnego nauczyciela jest ponadczasowy, ilustruje poniższa współczesna historia.
Matematyczka, przezywana przez uczniów Fibonaccią (czytaj: Fibonacią) z częstotliwością demaskującą jej wredny charakter zadaje swoim uczniom w klasie następujące zadanie rachunkowe:
Zadanie. Wybierz według uznania dwie liczby naturalne 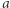 oraz
oraz 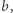 przy czym niech
przy czym niech 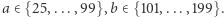 Następnie oblicz i starannie zapisz w zeszycie pierwsze
Następnie oblicz i starannie zapisz w zeszycie pierwsze 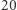 wyrazów ciągu danego rekurencyjnie
wyrazów ciągu danego rekurencyjnie
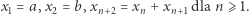 |
Po zebraniu zeszytów ocenia rozwiązania według schematu: odczytuje 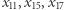 i sprawdza, czy
i sprawdza, czy
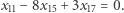
Jeśli tak, to zalicza rozwiązanie, a jeśli nie, to nie zalicza. Tak sobie życie upraszcza, że nie sprawdza w ogóle innych wyrazów ciągu 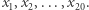 Czy godzi się tak postępować? Z tym pytaniem zwracam się do tych wszystkich, którzy nie mieli przyjemności być uczniami Fibonacci :)
Czy godzi się tak postępować? Z tym pytaniem zwracam się do tych wszystkich, którzy nie mieli przyjemności być uczniami Fibonacci :)
Jest też Fibonaccia II, bardziej znana jako czołowa aktywistka ruchu FPNW, która daje zniewalanym przez siebie uczniom jeszcze większą swobodę wyboru parametrów ciągu 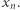 Prawi im tak:
Prawi im tak:
Zadanie. Wybierz dowolne liczby naturalne 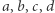 i wypisz wyrazy
i wypisz wyrazy 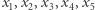 ciągu określonego rekurencyjnie:
ciągu określonego rekurencyjnie:
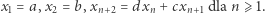 |
Czytelniku, jeżeli uważasz, że znasz się na ciągach, to jesteś wystarczająco postępowy, aby pomóc F II: podsuń jej wielomian 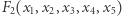 weryfikujący poprawność rachunku w tym sensie, że jeśli
weryfikujący poprawność rachunku w tym sensie, że jeśli 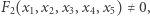 to na pewno uczeń coś pomylił!
to na pewno uczeń coś pomylił!
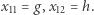 Jeśli dalej obliczał prawidłowo (przynajmniej do miejsca
Jeśli dalej obliczał prawidłowo (przynajmniej do miejsca 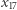 ), to uzyskał następujące wartości:
), to uzyskał następujące wartości: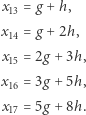
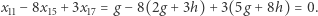
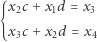
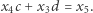
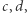 otrzyma
otrzyma
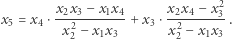
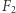 można więc przyjąć
można więc przyjąć