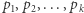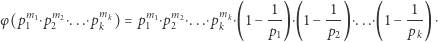Funkcja Eulera
Tym razem o kilku ciekawych własnościach funkcji Eulera.
Niech 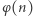 (gdzie
(gdzie  jest dodatnią liczbą naturalną) oznacza funkcję Eulera, czyli liczbę liczb naturalnych nie większych od
jest dodatnią liczbą naturalną) oznacza funkcję Eulera, czyli liczbę liczb naturalnych nie większych od  i względnie pierwszych z
i względnie pierwszych z 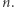 Na przykład
Na przykład
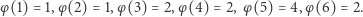 |
Przypomnijmy dwie powszechnie znane własności funkcji Eulera:
Twierdzenie (Eulera). Jeśli 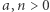 są liczbami naturalnymi oraz
są liczbami naturalnymi oraz 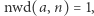 to
to 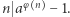
Zauważmy, że jeśli 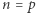 jest liczbą pierwszą i
jest liczbą pierwszą i 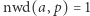 (czyli
(czyli 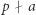 ), to wobec
), to wobec 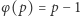 mamy podzielność
mamy podzielność  czyli tezę w małym twierdzeniu Fermata.
czyli tezę w małym twierdzeniu Fermata.
Nietrudno jest udowodnić, że dla 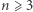 liczba
liczba 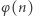 jest parzysta (Czytelniku, spróbuj sam!). Okazuje się, że nie każda liczba naturalna parzysta jest wartością funkcji Eulera
jest parzysta (Czytelniku, spróbuj sam!). Okazuje się, że nie każda liczba naturalna parzysta jest wartością funkcji Eulera 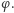 Andrzej Schinzel udowodnił, że dla żadnego naturalnego
Andrzej Schinzel udowodnił, że dla żadnego naturalnego 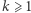 liczba
liczba 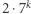 nie jest wartością funkcji
nie jest wartością funkcji 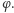
Jeśli 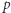 jest liczbą pierwszą, to
jest liczbą pierwszą, to 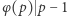 (bo
(bo  ). W 1932 roku Derrick Henry Lehmer spytał, czy istnieje taka liczba złożona
). W 1932 roku Derrick Henry Lehmer spytał, czy istnieje taka liczba złożona 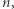 że
że 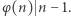 Pytanie to do dzisiaj pozostaje bez odpowiedzi. Można łatwo uzasadnić, że jeśli
Pytanie to do dzisiaj pozostaje bez odpowiedzi. Można łatwo uzasadnić, że jeśli 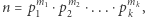 to podzielność
to podzielność  jest równoważna podzielności
jest równoważna podzielności
 |
(1) |
Oczywiście, gdy 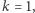 to powyższa podzielność zachodzi (wtedy
to powyższa podzielność zachodzi (wtedy 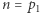 jest liczbą pierwszą). Dla
jest liczbą pierwszą). Dla  nie znaleziono liczb pierwszych
nie znaleziono liczb pierwszych 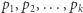 spełniających podzielność (1) i jest wątpliwe, czy takie liczby istnieją. W 1980 roku Geoffrey L. Cohen i Peter Hagis dowiedli, że jeśli
spełniających podzielność (1) i jest wątpliwe, czy takie liczby istnieją. W 1980 roku Geoffrey L. Cohen i Peter Hagis dowiedli, że jeśli  jest liczbą złożoną i zachodzi podzielność (1), to
jest liczbą złożoną i zachodzi podzielność (1), to 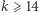 i
i 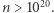
Zajmijmy się teraz równaniem
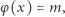 |
(2) |
gdzie 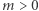 jest daną liczbą naturalną. Można udowodnić, że powyższe równanie
jest daną liczbą naturalną. Można udowodnić, że powyższe równanie
- (a)
- dla
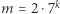 ma 0 rozwiązań,
ma 0 rozwiązań, - (b)
- dla
 ma 2 rozwiązania,
ma 2 rozwiązania, - (c)
- dla
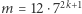 ma 3 rozwiązania.
ma 3 rozwiązania.
Zachodzi twierdzenie ogólne (Paul Erdős, Kevin Ford): dla każdej liczby naturalnej 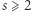 istnieje taka liczba naturalna
istnieje taka liczba naturalna 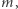 że równanie (2) ma dokładnie
że równanie (2) ma dokładnie  rozwiązań, co więcej, dla danego
rozwiązań, co więcej, dla danego 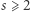 takich liczb jest nieskończenie wiele.
takich liczb jest nieskończenie wiele.
W 1922 roku Robert Daniel Carmichael sformułował hipotezę: nie istnieje takie 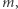 że równanie (2) ma dokładnie jedno rozwiązanie. Hipotezę można również wyrazić następująco: dla każdej liczby naturalnej
że równanie (2) ma dokładnie jedno rozwiązanie. Hipotezę można również wyrazić następująco: dla każdej liczby naturalnej 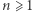 istnieje taka liczba naturalna
istnieje taka liczba naturalna 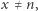 że
że 
W 1994 roku Aaron Schlafly i Stan Wagon, przeprowadzając obszerne obliczenia numeryczne, wykazali, że jeśli równanie 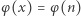 ma dokładnie jedno rozwiązanie (tj.
ma dokładnie jedno rozwiązanie (tj. 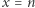 ), to
), to  tzn. najmniejszy kontrprzykład (jeśli istnieje) dla hipotezy Carmichaela ma ponad 10 milionów cyfr.
tzn. najmniejszy kontrprzykład (jeśli istnieje) dla hipotezy Carmichaela ma ponad 10 milionów cyfr.
Przejdźmy do równania
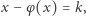 |
(3) |
gdzie 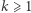 jest daną liczbą naturalną. Dla
jest daną liczbą naturalną. Dla 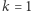 mamy nieskończenie wiele rozwiązań i są nimi wszystkie liczby pierwsze (dlaczego?). Dla
mamy nieskończenie wiele rozwiązań i są nimi wszystkie liczby pierwsze (dlaczego?). Dla 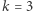 i
i 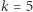 mamy rozwiązania odpowiednio
mamy rozwiązania odpowiednio 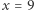 i
i  co Czytelnik zechce sprawdzić. Niech teraz
co Czytelnik zechce sprawdzić. Niech teraz 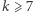 będzie dowolnie ustaloną liczbą nieparzystą. Na mocy wzmocnionej hipotezy Goldbacha (każda liczba większa od 6 jest sumą dwóch różnych liczb pierwszych) istnieją takie różne liczby pierwsze
będzie dowolnie ustaloną liczbą nieparzystą. Na mocy wzmocnionej hipotezy Goldbacha (każda liczba większa od 6 jest sumą dwóch różnych liczb pierwszych) istnieją takie różne liczby pierwsze 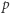 i
i  że
że 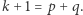 Przyjmijmy
Przyjmijmy 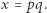 Wtedy
Wtedy 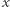 spełnia równanie (3), gdyż
spełnia równanie (3), gdyż
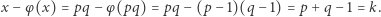 |
To pokazuje hipotetyczną rozwiązalność równania (3) dla każdego nieparzystego 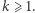
Okazuje się, że równanie (3) może nie mieć rozwiązania dla 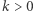 parzystych. Najmniejszymi takimi
parzystych. Najmniejszymi takimi 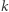 są: 10, 26, 34, 50, 52, 58, 86, 100. W 1995 roku Jerzy Browkin i Andrzej Schinzel udowodnili następujący
są: 10, 26, 34, 50, 52, 58, 86, 100. W 1995 roku Jerzy Browkin i Andrzej Schinzel udowodnili następujący
Fakt. Równanie
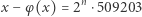 |
nie ma rozwiązań dla każdego naturalnego 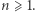
Na koniec kilka zadań dla Czytelnika.