Szereg Leibniza i punkty kratowe
Powiążemy tu wzór Leibniza

z geometrią (pola) i teorią liczb. Tekst jest wyraźnie dłuższy od tego, który jest w książce Hilberta i Cohn-Vossena, bo szkicujemy dowód twierdzenia z teorii liczb, na które autorzy jedynie powołują się. Pozostawimy jednak bez dowodu niektóre bardzo znane twierdzenia z teorii liczb, ze względu na ograniczenia miejsca w miesięczniku. Zaznaczyć warto, że podawany zwykle studentom pierwszego roku dowód jest krótszy, ale zdaniem autora tego tekstu, nie pokazuje związku z geometrią, który jest mocno sugerowany obecnością 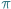 we wzorze.
we wzorze.
Używać będziemy liczb zespolonych. Jak zwykle 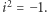 Symbol
Symbol ![|Z[i]](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/2x-481c0db8d938ad8f36f27b62baff09e50a8f82a8-im-33,33,33-FF,FF,FF.gif) oznacza zbiór liczb zespolonych, których części rzeczywista i urojona są całkowite. Liczby te nazywane są też punktami kratowymi.
oznacza zbiór liczb zespolonych, których części rzeczywista i urojona są całkowite. Liczby te nazywane są też punktami kratowymi.
Istotny dla dalszych rozważań jest fakt:
Fakt. Liczba całkowita 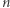 większa od
większa od 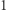 jest sumą kwadratów dwu liczb całkowitych wtedy i tylko wtedy, gdy jest iloczynem dwu sprzężonych elementów
jest sumą kwadratów dwu liczb całkowitych wtedy i tylko wtedy, gdy jest iloczynem dwu sprzężonych elementów ![|Z[i],](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/3x-7725d354fd58f8a57a6a4f755b87fefb1cd27edc-im-33,33,33-FF,FF,FF.gif) o modułach większych od
o modułach większych od 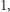 co wynika z równości
co wynika z równości 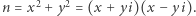
W ![Z[i]](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/1x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif) można zajmować się dzieleniem liczb nieomal tak, jak w zbiorze liczb całkowitych. Liczba
można zajmować się dzieleniem liczb nieomal tak, jak w zbiorze liczb całkowitych. Liczba ![|z1∈Z[i]](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/2x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif) jest dzielnikiem liczby
jest dzielnikiem liczby ![|z2∈ Z[i]](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/3x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif) wtedy i tylko wtedy, gdy istnieje taka liczba
wtedy i tylko wtedy, gdy istnieje taka liczba ![|q∈ Z[i],](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/4x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif) że
że 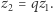 Liczba
Liczba 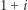 jest dzielnikiem liczby
jest dzielnikiem liczby 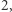 bo
bo 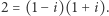 Jedynymi dzielnikami jedności w
Jedynymi dzielnikami jedności w ![Z[i],](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/9x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif) czyli dzielnikami liczby
czyli dzielnikami liczby 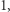 są
są 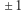 oraz
oraz 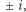 bo z równości
bo z równości 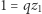 wynika, że
wynika, że 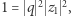 i z tego że
i z tego że ![|q,z1∈ Z[i]](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/15x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif) wynika, że
wynika, że 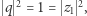 a jeśli
a jeśli 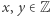 i
i 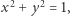 to
to 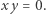 Liczbę pierwszą w
Liczbę pierwszą w ![Z[i]](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/20x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif) można zdefiniować jako taką, której jedynymi dzielnikami są dzielniki jedności oraz ona sama pomnożona przez jeden z dzielników jedności, ale sama nie jest dzielnikiem jedności. Wtedy
można zdefiniować jako taką, której jedynymi dzielnikami są dzielniki jedności oraz ona sama pomnożona przez jeden z dzielników jedności, ale sama nie jest dzielnikiem jedności. Wtedy 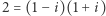 nie jest liczbą pierwszą, ale
nie jest liczbą pierwszą, ale 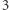 już jest (Czytelniku: dlaczego?). Prawdziwe jest, jak w przypadku podzielności w
już jest (Czytelniku: dlaczego?). Prawdziwe jest, jak w przypadku podzielności w 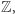
Twierdzenie (O jednoznaczności rozkładu na czynniki pierwsze). Jeśli ![|z∈ Z[i]](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/24x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif) nie jest dzielnikiem jedności, to istnieją liczby pierwsze
nie jest dzielnikiem jedności, to istnieją liczby pierwsze ![|p ,p ,...,p ∈ Z[i] 1 2 k](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/25x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif) takie, że
takie, że 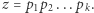 Jeśli liczby
Jeśli liczby ![˜p1,˜p2,...,˜pℓ∈ Z[i]](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/27x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif) są pierwsze i
są pierwsze i 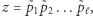 to
to 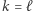 i po ewentualnej zmianie numeracji ilorazy
i po ewentualnej zmianie numeracji ilorazy 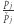 są dzielnikami jedności w
są dzielnikami jedności w ![|Z[i].](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/31x-a1174a9f91cd68447e81c739a6a4b60a88b2399b-im-33,33,33-FF,FF,FF.gif)
Dowód można oprzeć na następującym, nietrudnym do uzasadnienia, fakcie.
Twierdzenie (O dzieleniu z resztą w ![| Z[i]](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/1x-d21fbcfdcf7e366e7be0adcf66f382a2c7058eee-im-33,33,33-FF,FF,FF.gif) ). Dla dowolnych liczb
). Dla dowolnych liczb 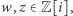
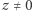 istnieją liczby
istnieją liczby ![κ,ρ ∈ Z[i]](/math/temat/matematyka/teoria_liczb/2018/12/28/Szereg_Leibniza_i_punkty_kratowe/4x-d21fbcfdcf7e366e7be0adcf66f382a2c7058eee-im-33,33,33-FF,FF,FF.gif) takie, że
takie, że 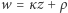 i
i 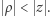 Liczbę
Liczbę  nazywamy ilorazem, a
nazywamy ilorazem, a 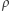 resztą z dzielenia liczby
resztą z dzielenia liczby 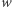 przez liczbę
przez liczbę 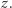
Obecność 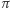 we wzorze Leibniza sugeruje, że w którymś momencie naszych rozważań powinien pojawić się okrąg.
we wzorze Leibniza sugeruje, że w którymś momencie naszych rozważań powinien pojawić się okrąg.
Twierdzenie (O podwajaniu sumy kwadratów). Na okręgu o promieniu 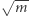 i środku 0 znajduje się tyle samo punktów kratowych, co na okręgu o promieniu
i środku 0 znajduje się tyle samo punktów kratowych, co na okręgu o promieniu 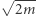 i środku
i środku 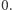
Dowód. Jeśli 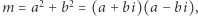 to
to
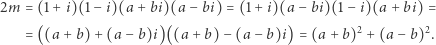 |
Jeśli zaś 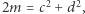 to obie liczby
to obie liczby 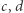 są parzyste albo obie są nieparzyste. W obu sytuacjach liczby
są parzyste albo obie są nieparzyste. W obu sytuacjach liczby 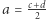 i
i 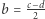 są całkowite i oczywiście
są całkowite i oczywiście 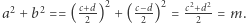 Innymi słowy, przypisując każdemu punktowi kratowemu
Innymi słowy, przypisując każdemu punktowi kratowemu 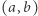 punkt
punkt 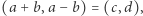 określamy różnowartościowe przekształcenie zbioru wszystkich punktów kratowych na zbiór wszystkich punktów kratowych, których obydwie współrzędne dają tę samą resztę z dzielenia przez
określamy różnowartościowe przekształcenie zbioru wszystkich punktów kratowych na zbiór wszystkich punktów kratowych, których obydwie współrzędne dają tę samą resztę z dzielenia przez 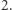 Przy tym punktom z okręgu o promieniu
Przy tym punktom z okręgu o promieniu 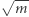 przypisywane są punkty z okręgu o promieniu
przypisywane są punkty z okręgu o promieniu 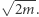
- Cały artykuł dostępny jest w wersji do druku [application/pdf]: (467 KB)