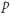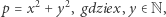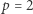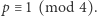Twierdzenia Fermata różnej wielkości

Pierre de Fermat (1601-1665)
Pierre de Fermat był Francuzem i żył w pierwszej połowie XVII wieku (1601-1665). Jako radca prawny praktykował w sądzie w Tuluzie na południu Francji. Naukami ścisłymi, a w szczególności matematyką, interesował się jako amator, ale wniósł potężny wkład do ich rozwoju. Szczególnie spektakularne są jego osiągnięcia w teorii liczb i o nich traktuje niniejszy artykuł. Wszyscy wiedzą, że jest Wielkie Twierdzenie Fermata (WTwF), Małe Twierdzenie Fermata (MTwF) i jeszcze inne twierdzenia Fermata dotyczące teorii liczb - ale które z nich jest największe?
Liczby fascynowały człowieka na długo przed Fermatem, a właściwie to już od jego zejścia z drzewa. Z tego długiego okresu uwzględnimy tylko Diofantosa, tworzącego (a zatem żyjącego) w starożytnej Grecji, gdyż jest on jednym z bohaterów opowiadanej historii. Najważniejszymi aktorami są jednak tytułowe twierdzenia. Oto one.
Twierdzenie (Małe Twierdzenie Fermata). Jeśli 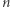 jest liczbą pierwszą oraz
jest liczbą pierwszą oraz 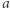 jest liczbą całkowitą niepodzielną przez
jest liczbą całkowitą niepodzielną przez 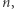 to
to
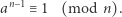 |
(1) |
W obecnej erze komputerów małe twierdzenie Fermata bywa stosowane do sprawdzania, czy dana (duża) liczba naturalna 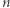 jest pierwsza. Zilustrujemy to na przykładzie. Niech
jest pierwsza. Zilustrujemy to na przykładzie. Niech

Jak sprawdzić, czy liczba 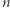 jest pierwsza? Można, oczywiście, dzielić ją przez kolejne liczby naturalne
jest pierwsza? Można, oczywiście, dzielić ją przez kolejne liczby naturalne 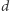 i czekać na przypadek, że dzielenie da się wykonać bez reszty. Wtedy
i czekać na przypadek, że dzielenie da się wykonać bez reszty. Wtedy 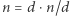 i liczba
i liczba 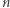 jest, oczywiście, złożona. Wystarczy używać
jest, oczywiście, złożona. Wystarczy używać 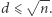 W naszym przypadku
W naszym przypadku 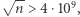 a zatem grozi nam wiele dzieleń z resztą, chyba że
a zatem grozi nam wiele dzieleń z resztą, chyba że 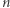 ma mały dzielnik
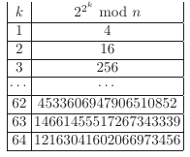
ma mały dzielnik 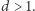 Obok przedstawiono istotny fragment tabeli, w której przedstawiono reszty liczb
Obok przedstawiono istotny fragment tabeli, w której przedstawiono reszty liczb 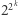 przy dzieleniu przez
przy dzieleniu przez  dla
dla 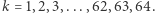
Mamy zatem

i to na mocy małego twierdzenia Fermata kończy dowód, że  nie jest liczbą pierwszą. Proszę zauważyć, że przeprowadzone rachunki nie dają żadnego nietrywialnego dzielnika
nie jest liczbą pierwszą. Proszę zauważyć, że przeprowadzone rachunki nie dają żadnego nietrywialnego dzielnika 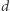 liczby
liczby 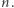 Używając innych metod, można pokazać, że
Używając innych metod, można pokazać, że

jest rozkładem 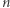 na czynniki pierwsze. Niestety, są liczby złożone
na czynniki pierwsze. Niestety, są liczby złożone 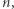 które bardzo sprytnie podszywają się pod liczby pierwsze - to tak zwane liczby Carmichaela. Liczbę złożoną
które bardzo sprytnie podszywają się pod liczby pierwsze - to tak zwane liczby Carmichaela. Liczbę złożoną 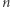 nazywamy liczbą Carmichaela, gdy dla każdej liczby całkowitej
nazywamy liczbą Carmichaela, gdy dla każdej liczby całkowitej  względnie pierwszej z
względnie pierwszej z  zachodzi kongruencja (1). Najmniejszą taką liczbą jest
zachodzi kongruencja (1). Najmniejszą taką liczbą jest 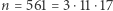 i wiadomo, że jest ich nieskończenie wiele.
i wiadomo, że jest ich nieskończenie wiele.
O MTwF można by mówić w nieskończoność - należy więc przejść do omówienia Wielkiego Twierdzenia Fermata. Na marginesie czytanej książki Diofantosa Fermat zanotował zdanie równoważne następującemu
Twierdzenie (Wielkie Twierdzenie Fermata). Jeśli liczby całkowite dodatnie 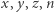 spełniają warunek
spełniają warunek 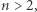 to na pewno
to na pewno

Nieudane próby udowodnienia (lub obalenia) tej hipotezy były podejmowane do 1993 roku, kiedy to wreszcie pełny dowód podał Andrew Wiles z Cambridge. Wielokrotnie i wyczerpująco opisywano, jak te wysiłki przyczyniły się do rozwoju współczesnej matematyki, przynajmniej w jej części algebraicznej i geometrycznej. My ograniczymy się do zaprezentowania jednego podejścia, które dość szybko okazuje się zupełnie nieskuteczne, ale co zaskakujące, również ono wpłynęło na rozwój matematyki! Oprócz równania rozważymy także kongruencję
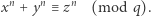 |
(2) |
Wówczas WTwF dla wykładnika 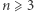 wynika łatwo z następującego lematu.
wynika łatwo z następującego lematu.
Lemat. Jeśli 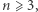 to dla nieskończenie wielu liczb pierwszych
to dla nieskończenie wielu liczb pierwszych 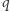 wszystkie rozwiązania kongruencji (2) spełniają
wszystkie rozwiązania kongruencji (2) spełniają 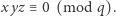
Rzeczywiście, rozważmy hipotetyczne rozwiązanie równania 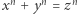 w liczbach całkowitych dodatnich i liczbę pierwszą
w liczbach całkowitych dodatnich i liczbę pierwszą 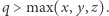 Wówczas kongruencja (2) ma, oczywiście, rozwiązanie, w którym żadna z liczb
Wówczas kongruencja (2) ma, oczywiście, rozwiązanie, w którym żadna z liczb 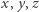 nie jest podzielna przez
nie jest podzielna przez 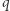 - ta konstatacja jest jednak sprzeczna z tezą Lematu.
- ta konstatacja jest jednak sprzeczna z tezą Lematu.
Niestety, taki atak na WTwF nie może się udać! Pokażemy teraz na dwa sposoby, że powyższy Lemat nie jest prawdziwy.
Pierwszy sposób oparty jest na słynnym twierdzeniu Schura.
Twierdzenie (Schur). Załóżmy, że liczby 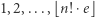 podzielono na
podzielono na  (rozłącznych) klas. Wówczas przynajmniej jedna z tych klas zawiera dwie liczby
(rozłącznych) klas. Wówczas przynajmniej jedna z tych klas zawiera dwie liczby 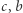 oraz ich różnicę
oraz ich różnicę 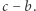
Stosując twierdzenie Schura, wykażemy przykładowo, że Lemat nie jest prawdziwy dla 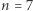 (dla dowolnego
(dla dowolnego 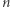 rozumowanie jest analogiczne). Rozróżniamy dwa przypadki:
rozumowanie jest analogiczne). Rozróżniamy dwa przypadki:
- (1)
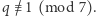 Wówczas funkcja
Wówczas funkcja 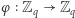 dana wzorem
dana wzorem 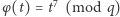 jest różnowartościowa (a więc i "na"). Istotnie, załóżmy przeciwnie, że dla pewnych
jest różnowartościowa (a więc i "na"). Istotnie, załóżmy przeciwnie, że dla pewnych 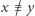 mamy
mamy 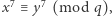 czyli
czyli 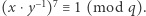 To jednak jest niemożliwe, bo
To jednak jest niemożliwe, bo 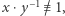 a 7 nie dzieli
a 7 nie dzieli 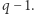 Oznacza to, że każda reszta modulo
Oznacza to, że każda reszta modulo 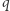 jest siódmą potęgą, a zatem kongruencja (2) ma mnóstwo nietrywialnych rozwiązań. Oznacza to, że każda reszta mod
jest siódmą potęgą, a zatem kongruencja (2) ma mnóstwo nietrywialnych rozwiązań. Oznacza to, że każda reszta mod 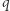 jest siódmą potęgą, a zatem kongruencja (2) ma mnóstwo nietrywialnych rozwiązań.
jest siódmą potęgą, a zatem kongruencja (2) ma mnóstwo nietrywialnych rozwiązań.- (2)
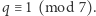 Tutaj załóżmy, że
Tutaj załóżmy, że 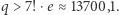 Liczby
Liczby 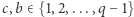 zaliczamy do tej samej klasy, gdy (z definicji) kongruencja
zaliczamy do tej samej klasy, gdy (z definicji) kongruencja 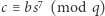 ma rozwiązanie. Jest
ma rozwiązanie. Jest 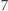 klas (abstrakcji) i na mocy twierdzenia Schura
klas (abstrakcji) i na mocy twierdzenia Schura 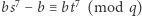 dla pewnych
dla pewnych 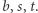 Mamy więc
Mamy więc 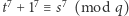 i, oczywiście,
i, oczywiście, 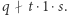
A oto kolejny dowód na to, że rzekoma teza Lematu nie jest prawdziwa. Tym razem rozumowanie korzysta ze słynnego oszacowania na liczbę rozwiązań kongruencji. Ogólna wersja tego oszacowania dla dowolnych gładkich rozmaitości nad ciałem skończonym, znana w ramach hipotez Weila jako hipoteza Riemanna dla rozmaitości, opierała się wysiłkom matematyków przez wiele lat. W końcu udowodnił ją w całej okazałości Pierre Deligne w 1973 roku i zastosował w tym dowodzie cały arsenał nowoczesnej geometrii algebraicznej.
Twierdzenie (Oszacowanie Hasse-Weila dla krzywej Fermata). Dla każdej liczby pierwszej 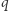 niech
niech 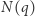 oznacza liczbę rozwiązań
oznacza liczbę rozwiązań 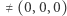 kongruencji (2), przy czym dwa rozwiązania
kongruencji (2), przy czym dwa rozwiązania 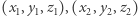 utożsamiamy, gdy istnieje takie
utożsamiamy, gdy istnieje takie 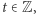 że
że

Wówczas mamy oszacowanie

Wynika stąd natychmiast, że dla ustalonego  i dla dostatecznie dużej liczby pierwszej
i dla dostatecznie dużej liczby pierwszej 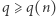 istnieją rozwiązania kongruencji (2) spełniające
istnieją rozwiązania kongruencji (2) spełniające 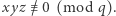
Po dwakroć zatem porzućmy wszelkie nadzieje na to, że WTwF można udowodnić poprzez rozważanie kongruencji. Z drugiej strony zarówno twierdzenie Schura, jak i powyższy szczególny przypadek hipotez Weila dla krzywych nad ciałami skończonymi, wywarły duży wpływ na rozwój kombinatoryki i geometrii algebraicznej. Tak więc pomysły, które całkowicie zawodzą w potencjalnie słynnym zastosowaniu, okazują swoją użyteczność jako zalążki nowych interesujących teorii.
I wreszcie, last but not least, omówimy twierdzenie Fermata bezprzymiotnikowe. Dotyczy ono przedstawialności liczb pierwszych w postaci sumy dwóch kwadratów liczb całkowitych.
Jedyna i istotna trudność w dowodzie tego twierdzenia to pokazanie, że każda liczba pierwsza 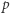 postaci
postaci 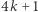 jest postaci (3). Czasem dopowiada się, że przedstawienie (3) jest tylko jedno, ale to jest łatwe. Powyższe wspaniałe twierdzenie Fermata jest zaczynem algebraicznej teorii liczb, jednego z ważnych działów matematyki współczesnej głównego nurtu.
jest postaci (3). Czasem dopowiada się, że przedstawienie (3) jest tylko jedno, ale to jest łatwe. Powyższe wspaniałe twierdzenie Fermata jest zaczynem algebraicznej teorii liczb, jednego z ważnych działów matematyki współczesnej głównego nurtu.
Mianowicie, twierdzenie to można sformułować tak:
- jeśli liczba pierwsza
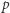 jest postaci
jest postaci 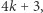 to
to 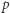 jest elementem nierozkładalnym w pierścieniu
jest elementem nierozkładalnym w pierścieniu ![Z[i] = {a + bi a, b∈ Z},](/math/temat/matematyka/teoria_liczb/2018/09/30/Twierdzenia_Fermata_roznej_wielk/5x-71f823a0abddf33838bae405bba122e42844f423-im-33,33,33-FF,FF,FF.gif)
- jeśli liczba pierwsza
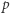 nie jest postaci
nie jest postaci 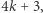 to jest elementem rozkładalnym w
to jest elementem rozkładalnym w ![|Z[i],](/math/temat/matematyka/teoria_liczb/2018/09/30/Twierdzenia_Fermata_roznej_wielk/9x-71f823a0abddf33838bae405bba122e42844f423-im-33,33,33-FF,FF,FF.gif) tzn.
tzn.
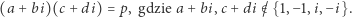 |
(4) |
Rzeczywiście, z (4) wynika, że

skąd po pomnożeniu obu ostatnich wzorów stronami otrzymujemy

Ponieważ 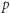 jest liczbą pierwszą, więc musi być
jest liczbą pierwszą, więc musi być

Odwrotnie, jeśli 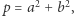 to liczba
to liczba 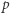 jest rozkładalna w
jest rozkładalna w ![| Z[i],](/math/temat/matematyka/teoria_liczb/2018/09/30/Twierdzenia_Fermata_roznej_wielk/17x-71f823a0abddf33838bae405bba122e42844f423-im-33,33,33-FF,FF,FF.gif) gdyż
gdyż

Prawa rozkładu liczb pierwszych w innych pierścieniach typu ![√--- Z[ − d]](/math/temat/matematyka/teoria_liczb/2018/09/30/Twierdzenia_Fermata_roznej_wielk/19x-71f823a0abddf33838bae405bba122e42844f423-im-33,33,33-FF,FF,FF.gif) wiążą się w subtelny sposób z próbami przeniesienia powyższego twierdzenia Fermata na przedstawienia typu
wiążą się w subtelny sposób z próbami przeniesienia powyższego twierdzenia Fermata na przedstawienia typu

Z powyżej napisanego nie wynika w żaden sposób, które z omówionych teorioliczbowych twierdzeń Fermata jest największe. Wierzę jednak, że każde z nich potrafi zainfekować Czytelnika teorią liczb równie mocno, a o to tylko tu chodzi.