Jak powstały wszystko opisujące liczby
Pierwszy etap pitagoreizmu głosił hasło wszystko jest liczbą: pożądaną Harmonię Świata da się wyrazić jako stosunek liczb (dziś nazywanych naturalnymi), przy czym jest ona tym pełniejsza, im liczby te są mniejsze.
Wykrycie, iż stosunek przekątnej kwadratu do jego boku nie da się opisać w ten sposób, spowodował kryzys, w którego wyniku od kultu liczb odstąpiono (liczby zostawmy kupczykom), wiążąc Harmonię z proporcjami geometrycznymi i złotą proporcję wynosząc na ołtarze. Ten drugi etap pitagoreizmu uformował geometrię naszej cywilizacji w kształcie, jaki ma ona do dziś.
Ale owe lękliwe porzucenie liczb nie mogło podobać się ambitnym uczniom Akademii Platońskiej. I faktycznie je przełamali. Stworzyli w tym celu pierwszą w dziejach teorię aksjomatyczną - była to teoria wielkości jednego rodzaju. Oto jej aksjomaty:
- Wielkości jednego rodzaju dają się porównać (a więc mamy zawsze
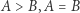 lub
lub 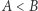 );
); - Dla dwóch wielkości jednego rodzaju istnieje wielkość tegoż rodzaju, będąca ich sumą;
- Istnieje wielkość uzupełniająca mniejszą z wielkości do większej;
- Wielkość można
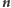 -krotnie zwielokrotnić dla każdego naturalnego
-krotnie zwielokrotnić dla każdego naturalnego 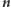 ;
; - Dowolną wielkość
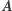 można zwielokrotnić tak, by okazała się większa od z góry danej wielkości
można zwielokrotnić tak, by okazała się większa od z góry danej wielkości 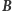 ,
,
ten ostatni warunek został później nazwany aksjomatem Archimedesa.
Dalej pomysły poszły już dwiema, zdecydowanie odmiennymi, drogami.
Teajtetos (-410; -368) stworzył to, co dziś nazywamy algorytmem Euklidesa. Mianowicie stwierdził, że stosunek dwóch wielkości jednego rodzaju można opisać za pomocą poniższej procedury:
Procedura ta czasami się kończy (w przypadku liczb naturalnych zawsze), a czasami nie (przykłady dalej). Zawsze natomiast zamienia stosunek wielkości 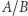 na specyficzny ciąg liczb naturalnych
na specyficzny ciąg liczb naturalnych 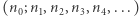 zwany ułamkiem ciągłym lub łańcuchowym. Tak można wyrazić stosunek dowolnych dwóch wielkości jednego rodzaju (np. długości, ciężaru, pola powierzchni itp.), a więc każdą (dodatnią) liczbę rzeczywistą.
zwany ułamkiem ciągłym lub łańcuchowym. Tak można wyrazić stosunek dowolnych dwóch wielkości jednego rodzaju (np. długości, ciężaru, pola powierzchni itp.), a więc każdą (dodatnią) liczbę rzeczywistą.
W przykładzie liczbowym będzie to 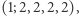 czasami zapisywane pretensjonalnie jako
czasami zapisywane pretensjonalnie jako

Zapis taki jest przydatny (jak będzie widać dalej), a powstaje on z inaczej zapisanego algorytmu Euklidesa: wyłączmy całości, resztę (mniejszą wobec tego od 1) odwracamy, wyłączamy całości, resztę odwracamy, wyłączamy i tak dalej. Widać to obok.

Zobaczmy, jak to działa w tym najbardziej wówczas nerwowym punkcie - w przypadku stosunku przekątnej kwadratu do jego boku. Narysujmy ćwiartkę okręgu o środku 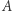 i promieniu
i promieniu 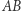 (rysunek), a następnie styczną do niego w punkcie
(rysunek), a następnie styczną do niego w punkcie 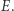 Jak łatwo zauważyć, powstały cztery odcinki równej długości
Jak łatwo zauważyć, powstały cztery odcinki równej długości 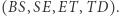 Gdy narysujemy półokrąg o środku
Gdy narysujemy półokrąg o środku 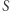 i promieniu
i promieniu 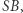 powstanie jeszcze jeden odcinek o tej długości:
powstanie jeszcze jeden odcinek o tej długości: 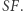 Przystąpmy teraz do rachunków.
Przystąpmy teraz do rachunków.

Wyjaśnienia wymaga jedynie ostatnia z równości. Bierze się ona stąd, że trójkąty 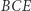 i
i 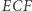 są podobne (kąt przy wierzchołku
są podobne (kąt przy wierzchołku 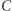 jest wspólny, a
jest wspólny, a 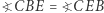 jako kąt wpisany i dopisany oparte na łuku
jako kąt wpisany i dopisany oparte na łuku 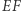 ).
).
Z przeprowadzonego rachunku wynika, że sytuacja będzie się powtarzać bez końca, a więc stosunek przekątnej kwadratu do jego boku to ułamek łańcuchowy zaczynający się od 1 i mający następnie nieskończony ciąg dwójek, co zapisuje się 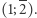
Oczywiście (żyjąc ponad dwa tysiące lat później) możemy to zrealizować, rozwijając 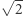 w ułamek łańcuchowy:
w ułamek łańcuchowy:

Ułamki łańcuchowe były przyjęte bardzo sympatycznie, bo nawiązywały do opisu Harmonii przez liczby naturalne - najbardziej harmoniczna była złota proporcja, gdyż opisywały ją same jedynki 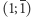 :
:

Ułamki łańcuchowe mają szereg interesujących własności, np.:
- jak można było zauważyć z przykładu liczbowego, liczby wymierne rozwijają się w ułamki skończone;
- ułamki okresowe są pierwiastkami równań kwadratowych o współczynnikach wymiernych;
- niewymierne pierwiastki kwadratowe z liczb wymiernych rozwijają się w ułamki w pewnym stopniu symetryczne, a mianowicie postaci
 ;
;
Ponieważ to dziwne, rozpatrzmy przykład ułamka 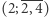 : oznaczmy
: oznaczmy 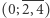 przez
przez 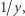 wówczas
wówczas

czyli 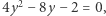 wobec tego
wobec tego

oraz

Poważniejszą własność ułamków łańcuchowych odkrył w XVIII wieku Lagrange:
Twierdzenie. Redukt ułamka łańcuchowego liczby n jest jej najlepszym wymiernym przybliżeniem.
Sformułowanie to wymaga objaśnienia terminu najmniejsze wymierne przybliżenie, niezgodnego z naszymi przyzwyczajeniami językowymi. Otóż jest to takie przybliżenie wymierne, że lepsze od niego musi mieć większy mianownik.
Tak więc z podanego przy algorytmie Euklidesa przykładu liczbowego wynika, że jednym z najlepszych przybliżeń wymiernych 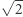 jest
jest 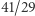 (to skrócone
(to skrócone 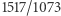 ), ale też
), ale też 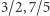 czy
czy 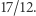
Skoro propozycja opisania liczb rzeczywistych za pomocą ułamków łańcuchowych jest tak atrakcyjna, to czemu uczymy się zupełnie innego sposobu patrzenia na nie?
Jakąś częścią odpowiedzi jest fakt, że była też inna propozycja, przedstawiona przez Eudoksosa 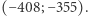 On nie przedstawiał proporcji wielkości jednego rodzaju za pomocą ciągu liczb naturalnych, lecz opisywał ją poprzez jej dolne i górne przybliżenia wymierne. A robił to tak.
On nie przedstawiał proporcji wielkości jednego rodzaju za pomocą ciągu liczb naturalnych, lecz opisywał ją poprzez jej dolne i górne przybliżenia wymierne. A robił to tak.
Proporcja wielkości jednego rodzaju 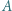 i
i 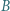 jest równa proporcji wielkości jednego (ale możliwe, że zupełnie innego) rodzaju
jest równa proporcji wielkości jednego (ale możliwe, że zupełnie innego) rodzaju 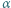 i
i 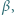 gdy dla dowolnych liczb naturalnych
gdy dla dowolnych liczb naturalnych  i
i 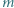 zachodzą warunki:
zachodzą warunki:
jeśli 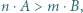 to
to 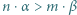 ;
;
jeśli 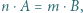 to
to 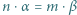 ;
;
jeśli 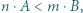 to
to 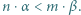
A gdzie tu są zapowiadane przybliżenia wymierne? Popatrzmy na to tak, zakładając przez chwilę, że zachodzi pierwsza sytuacja:

zatem 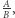 jak i
jak i 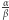 mają takie same wymierne przybliżenia dolne.
mają takie same wymierne przybliżenia dolne.
Trzeci przypadek wskazuje, że 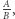 jak i
jak i 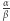 mają te same przybliżenia górne.
mają te same przybliżenia górne.
Łącznie więc proporcja jest wyznaczona przez zbiór wszystkich swoich wymiernych przybliżeń dolnych i przybliżeń górnych. Coś takiego nazywamy dziś przekrojem Dedekinda i to jest obowiązujący od stuleci sposób uprawiania liczb rzeczywistych.
Dziś może nam być trudno wyobrazić sobie świat bez - niejako danych nam od urodzenia - liczb rzeczywistych. Wyobraźmy sobie jednak, że ich nie ma i wykażmy za Euklidesem (VI księga Elementów), że
Twierdzenie. Stosunek pól dwóch trójkątów o równych wysokościach jest równy stosunkowi ich podstaw (pamiętajmy: pola i odcinki to są wielkości różnych rodzajów).
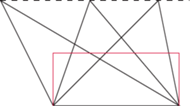
Najpierw spostrzeżenie pomocnicze: pola trójkątów o równych wysokościach i podstawach są równe - dowodzi się go nożyczkami (Czytelniku, czy masz nożyczki?), rozcinając każdy taki trójkąt na trzy kawałki i składając z niego prostokąt o jednym boku równym podstawie, a drugim - połowie wysokości.
Skoro tak, to możemy dwa trójkąty, o których mówi twierdzenie, narysować jako prostokątne. I możemy je zestawić tak, aby ich równe (bo równe wspólnej wysokości) przyprostokątne pokryły się.
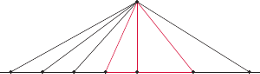
Teraz odkładamy  razy w lewo podstawę lewego trójkąta i
razy w lewo podstawę lewego trójkąta i 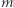 razy w prawo podstawę prawego trójkąta. Otrzymane punkty łączymy z górnym wierzchołkiem wspólnej przyprostokątnej, otrzymując na lewo
razy w prawo podstawę prawego trójkąta. Otrzymane punkty łączymy z górnym wierzchołkiem wspólnej przyprostokątnej, otrzymując na lewo  trójkątów o polach równych lewemu kolorowemu trójkątowi, a na prawo
trójkątów o polach równych lewemu kolorowemu trójkątowi, a na prawo 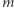 trójkątów o polach równych kolorowemu prawemu trójkątowi (tu
trójkątów o polach równych kolorowemu prawemu trójkątowi (tu 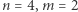 ).
).
Gdy złożymy rysunek wzdłuż wspólnej przyprostokątnej, to  -krotna lewa podstawa będzie większa od
-krotna lewa podstawa będzie większa od 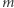 -krotnej prawej wtedy i tylko wtedy, gdy
-krotnej prawej wtedy i tylko wtedy, gdy 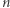 -krotne lewe pole będzie większe od
-krotne lewe pole będzie większe od 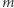 -krotnego pola prawego.
-krotnego pola prawego.
***
Wynalazek liczb rzeczywistych to, zdaniem wielu, największy wynalazek matematyczny wszech czasów. Nad pomysłem Eudoksosa rozpływali się w zachwycie zwłaszcza Archimedes i - wiele lat później - Newton. Ten ostatni swój podziw wyrażał, podkreślając, że nie jest możliwe podzielenie rozciągłości w przestrzeni przez rozciągłość w czasie, bo to zupełnie inne rzeczy - jest natomiast możliwe podzielenie liczby mierzącej rozciągłość w przestrzeni przez liczbę mierzącą rozciągłość w czasie - bo to takie same liczby! W wyniku dzielenia otrzymamy wówczas liczbę, której znaczenie (w tym przypadku zapewne prędkość) musimy ustalić.
Tak więc liczby rzeczywiste pozwoliły na zastosowanie matematyki do wszelkich zjawisk, bo każde z nich opisujemy tymi samymi liczbami (co faktycznie w koncepcji Eudoksosa lepiej widać).