Konsekwencje twierdzenia Dirichleta
Słynne twierdzenie Dirichleta głosi, że jeżeli liczby naturalne 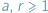 są względnie pierwsze, to ciąg arytmetyczny
są względnie pierwsze, to ciąg arytmetyczny 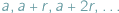 zawiera nieskończenie wiele liczb pierwszych. Przedstawimy kilka wniosków płynących z tego twierdzenia.
zawiera nieskończenie wiele liczb pierwszych. Przedstawimy kilka wniosków płynących z tego twierdzenia.
Wniosek (A). W każdym takim ciągu dla każdej liczby naturalnej  istnieje nieskończenie wiele wyrazów będących iloczynami
istnieje nieskończenie wiele wyrazów będących iloczynami  różnych liczb pierwszych. Dowód tego stwierdzenia można znaleźć w książeczce Wacława Sierpińskiego "250 zadań z elementarnej teorii liczb" (WSiP, Warszawa 1986, zadanie nr 70).
różnych liczb pierwszych. Dowód tego stwierdzenia można znaleźć w książeczce Wacława Sierpińskiego "250 zadań z elementarnej teorii liczb" (WSiP, Warszawa 1986, zadanie nr 70).
Wniosek (B). Dla każdej liczby naturalnej 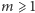 istnieje taka liczba pierwsza
istnieje taka liczba pierwsza 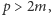 że przedziały
że przedziały 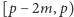 i
i ![(p, p+ 2m]](/math/temat/matematyka/teoria_liczb/2018/02/26/Konsekwencje_twierdzenia_Dirichleta/4x-539729a881729636ebaf71a5c06912584176feef-im-33,33,33-FF,FF,FF.gif) nie zawierają liczby pierwszej. Dowód powyższego stwierdzenia znajduje się w moim artykule Tryptyk o liczbach pierwszych w
nie zawierają liczby pierwszej. Dowód powyższego stwierdzenia znajduje się w moim artykule Tryptyk o liczbach pierwszych w 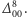
Wniosek (C). Jeżeli w takim ciągu pewien wyraz jest 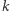 -tą potęgą liczby naturalnej, to ciąg ten zawiera nieskończenie wiele
-tą potęgą liczby naturalnej, to ciąg ten zawiera nieskończenie wiele 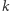 -tych potęg liczb pierwszych.
-tych potęg liczb pierwszych.
Dowód Andrzeja Schinzla (korespondencja prywatna). Załóżmy, że 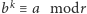 dla pewnego
dla pewnego 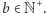 Skoro
Skoro 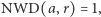 to wynika stąd, że
to wynika stąd, że 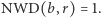 Zatem na mocy twierdzenia Dirichleta istnieje nieskończenie wiele takich liczb pierwszych
Zatem na mocy twierdzenia Dirichleta istnieje nieskończenie wiele takich liczb pierwszych 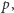 że
że 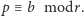 W konsekwencji
W konsekwencji 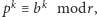 czyli
czyli 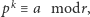 co kończy dowód.
co kończy dowód.
Wniosek (D). Dla dowolnej liczby naturalnej 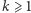 ciąg arytmetyczny
ciąg arytmetyczny 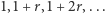 zawiera nieskończenie wiele
zawiera nieskończenie wiele 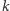 -tych potęg liczb pierwszych.
-tych potęg liczb pierwszych.
Uzasadnienie. Wystarczy zauważyć, że 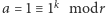 i skorzystać z poprzedniego wniosku.
i skorzystać z poprzedniego wniosku.
Wniosek (E). Niech 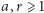 będą liczbami naturalnymi względnie pierwszymi. Wówczas dla każdej liczby naturalnej
będą liczbami naturalnymi względnie pierwszymi. Wówczas dla każdej liczby naturalnej 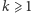 istnieje nieskończenie wiele takich par
istnieje nieskończenie wiele takich par 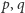 liczb pierwszych, że pewien wyraz ciągu arytmetycznego
liczb pierwszych, że pewien wyraz ciągu arytmetycznego 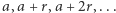 jest postaci
jest postaci 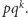
Dowód. Niech 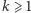 będzie dowolnie ustaloną liczbą naturalną. Niech
będzie dowolnie ustaloną liczbą naturalną. Niech 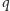 będzie dowolnie ustaloną liczbą pierwszą, niedzielącą
będzie dowolnie ustaloną liczbą pierwszą, niedzielącą 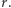 Skoro liczby
Skoro liczby 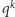 i
i  są wtedy względnie pierwsze, to istnieją takie liczby naturalne
są wtedy względnie pierwsze, to istnieją takie liczby naturalne 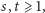 że
że
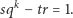 |
(*) |
Przy tym widać, że liczby  i
i  są względnie pierwsze. Ponadto z założenia liczby
są względnie pierwsze. Ponadto z założenia liczby  i
i  są względnie pierwsze. Wynika stąd, że
są względnie pierwsze. Wynika stąd, że 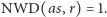 Zatem, wykorzystując twierdzenie Dirichleta, stwierdzamy, że ciąg arytmetyczny
Zatem, wykorzystując twierdzenie Dirichleta, stwierdzamy, że ciąg arytmetyczny 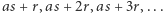 zawiera nieskończenie wiele liczb pierwszych. Niech więc
zawiera nieskończenie wiele liczb pierwszych. Niech więc 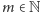 będzie takie, że
będzie takie, że 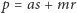 będzie liczbą pierwszą i przy tym takich liczb
będzie liczbą pierwszą i przy tym takich liczb 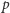 jest nieskończenie wiele. Połóżmy
jest nieskończenie wiele. Połóżmy 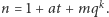 Wtedy
Wtedy 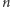 -ty wyraz ciągu arytmetycznego
-ty wyraz ciągu arytmetycznego 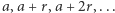 jest, wobec
jest, wobec 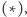 równy:
równy:

Wniosek (F). Istnieje nieskończenie wiele liczb pierwszych, których zapis dziesiętny kończy się na:
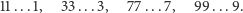 |
Dowód tej własności pozostawiam Czytelnikowi. Powodzenia!