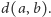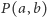Złociaków nigdy dosyć
Wyobraźmy sobie, że trafiliśmy do dziwnego kraju, w którym jedynymi dostępnymi środkami płatniczymi są monety o nominałach 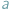 i
i 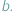 Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty. Nie chcąc tracić swoich złociaków, rozglądamy się za pysznościami w cenach
Formy płatności nie rozwinęły się na tyle, żeby płacić kartą lub czekiem, na domiar złego wybraliśmy się do cukierni, w której kasa jest zupełnie pusta i sprzedawca nie może wydać nam reszty. Nie chcąc tracić swoich złociaków, rozglądamy się za pysznościami w cenach 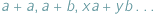 Niektórych kwot, oczywiście, nie daje się uzyskać z nominałów
Niektórych kwot, oczywiście, nie daje się uzyskać z nominałów 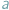 i
i 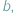 a niektóre można otrzymać na wiele sposobów.
a niektóre można otrzymać na wiele sposobów.
Dla wszystkich względnie pierwszych liczb naturalnych 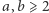 istnieje taka największa niewygodna kwota
istnieje taka największa niewygodna kwota 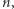 że wszystkie kolejne
że wszystkie kolejne  mogą być uzyskane za pomocą tych nominałów. Wyjaśnienie, że taka największa niewygodna
mogą być uzyskane za pomocą tych nominałów. Wyjaśnienie, że taka największa niewygodna  faktycznie istnieje, jej postać oraz parę innych obserwacji użytkowania tylko dwóch nominałów można znaleźć w
faktycznie istnieje, jej postać oraz parę innych obserwacji użytkowania tylko dwóch nominałów można znaleźć w  A teraz rzucimy na sprawę nowe światło.
A teraz rzucimy na sprawę nowe światło.
- (1)
-
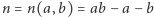 jest największą liczbą, która nie jest postaci
jest największą liczbą, która nie jest postaci 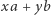 dla
dla 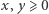 - mimo największych starań nie uzyskamy jej ze złociaków.
- mimo największych starań nie uzyskamy jej ze złociaków. - (2)
- Dokładnie połowa liczb ze zbioru
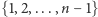 jest postaci
jest postaci
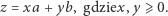
(  )
) - (3)
- Jeśli
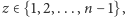 to dokładnie jedna z liczb:
to dokładnie jedna z liczb:  albo
albo 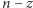 jest postaci (
jest postaci (  ).
).
Własności 1 i 2 zostały udowodnione w Delcie 4/2014. Z obu tych własności wynika własność 3 na mocy następującego rozumowania: nie może się zdarzyć, że dla pewnego 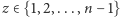 obie liczby
obie liczby  oraz
oraz 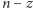 są postaci (
są postaci (  ), gdyż wówczas ich suma
), gdyż wówczas ich suma 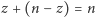 też byłaby postaci (
też byłaby postaci (  ), a to jest sprzeczne z własnością 1 (przecież
), a to jest sprzeczne z własnością 1 (przecież  to największa liczba, której nie jesteśmy w stanie uzyskać!). Tak więc obie
to największa liczba, której nie jesteśmy w stanie uzyskać!). Tak więc obie  i
i 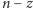 nie mogą jednocześnie być postaci (
nie mogą jednocześnie być postaci (  ) - zatem z własności 2 otrzymujemy, że w każdym zbiorze
) - zatem z własności 2 otrzymujemy, że w każdym zbiorze 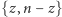 dokładnie jedna z liczb jest postaci (
dokładnie jedna z liczb jest postaci (  )!
)!
Dla 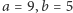 mamy
mamy 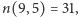 a liczby przedstawialne w postaci (
a liczby przedstawialne w postaci (  ) (ich zbiór oznaczmy przez
) (ich zbiór oznaczmy przez 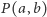 ), mniejsze od
), mniejsze od 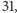 to
to

Natomiast liczby nieprzedstawialne w postaci (  ) mniejsze od
) mniejsze od 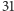 to
to

Już na tym prostym przykładzie można zauważyć, że istnieją dość długie ciągi kolejnych liczb naturalnych, z których każda jest przedstawialna. Zachodzi bowiem następujące twierdzenie.
Twierdzenie 1. Dla dowolnych względnie pierwszych 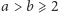 w zbiorze
w zbiorze 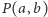 istnieje ciąg kolejnych
istnieje ciąg kolejnych 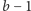 liczb naturalnych, ale nie istnieje taki ciąg długości
liczb naturalnych, ale nie istnieje taki ciąg długości 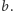
Dowód. Ponieważ liczby 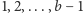 oczywiście nie są przedstawialne, więc na mocy własności 3 kolejne liczby
oczywiście nie są przedstawialne, więc na mocy własności 3 kolejne liczby 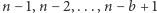 są przedstawialne. Gdyby w zbiorze
są przedstawialne. Gdyby w zbiorze 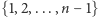 były kolejne liczby
były kolejne liczby 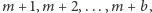 wszystkie należące do
wszystkie należące do 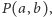 to na mocy własności 3 żadna z liczb
to na mocy własności 3 żadna z liczb 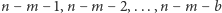 nie byłaby przedstawialna, co jednak jest sprzeczne z następującą obserwacją: odstępy między kolejnymi liczbami w
nie byłaby przedstawialna, co jednak jest sprzeczne z następującą obserwacją: odstępy między kolejnymi liczbami w 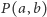 są nie większe od
są nie większe od 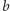 (rzeczywiście, jeśli
(rzeczywiście, jeśli 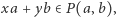 to następna liczba naturalna
to następna liczba naturalna  w
w 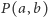 spełnia nierówność
spełnia nierówność 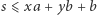 ).
).

W sformułowaniu kolejnego twierdzenia wielkość parametrów  nie odgrywa żadnej roli - w tym sensie ma ono charakter bardziej uniwersalny niż twierdzenie 1.
nie odgrywa żadnej roli - w tym sensie ma ono charakter bardziej uniwersalny niż twierdzenie 1.
Zanim je udowodnimy w ogólności, zobaczmy, jak to działa na naszym przykładzie. Ciąg 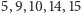 zawiera podciąg arytmetyczny
zawiera podciąg arytmetyczny 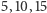 ; ciąg
; ciąg 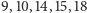 zawiera podciąg
zawiera podciąg  ; ciąg
; ciąg  zawiera podciąg
zawiera podciąg 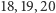 itd.
itd.
Dowód. Niech 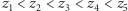 będą kolejnymi liczbami w
będą kolejnymi liczbami w  Dla każdego
Dla każdego 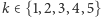 istnieją więc takie liczby całkowite nieujemne
istnieją więc takie liczby całkowite nieujemne 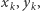 że
że

Każdej parze liczb 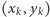 przyporządkujmy parę ich reszt modulo
przyporządkujmy parę ich reszt modulo  np. jeśli
np. jeśli 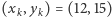 to otrzymujemy parę reszt
to otrzymujemy parę reszt 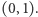 Ponieważ wszystkie pary reszt modulo
Ponieważ wszystkie pary reszt modulo 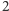 to:
to:  więc istnieją różne liczby
więc istnieją różne liczby 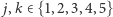 takie, że
takie, że  są tej samej parzystości oraz
są tej samej parzystości oraz 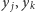 są tej samej parzystości. Wynika stąd, że liczba
są tej samej parzystości. Wynika stąd, że liczba


gdyż liczby  są kolejne w
są kolejne w 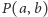 !
!
Zachęta. Zachęcamy Czytelnika do napisania programu, który dla danych liczb względnie pierwszych  będzie generował zbiory
będzie generował zbiory 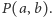 Wtedy można eksperymentować z różnymi konkretnymi parami
Wtedy można eksperymentować z różnymi konkretnymi parami 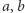 i na podstawie obserwacji dostrzegać różne prawidłowości. Niektóre z nich da się ująć w formę twierdzeń, czyli udowodnić - tak powstaje matematyka.
i na podstawie obserwacji dostrzegać różne prawidłowości. Niektóre z nich da się ująć w formę twierdzeń, czyli udowodnić - tak powstaje matematyka.
Pokusimy się o jeszcze jeden przykład. Skoro ostatnie 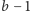 liczb z
liczb z 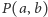 są kolejnymi liczbami naturalnymi (dowód twierdzenia 1), to można zapytać o takie najmniejsze
są kolejnymi liczbami naturalnymi (dowód twierdzenia 1), to można zapytać o takie najmniejsze  że obie liczby
że obie liczby  oraz
oraz 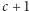 należą do
należą do 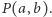 Wiemy, że
Wiemy, że 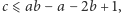 ale eksperymentując z różnymi wartościami
ale eksperymentując z różnymi wartościami 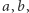 dochodzimy do następującej hipotezy.
dochodzimy do następującej hipotezy.
Hipoteza. Dla danych liczb względnie pierwszych 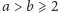 definiujemy
definiujemy 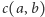 jako taką najmniejszą liczbę naturalną
jako taką najmniejszą liczbę naturalną 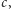 że obie liczby
że obie liczby 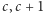 należą do
należą do 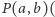 tzn. mają postać (
tzn. mają postać (  )). Wówczas
)). Wówczas  można otrzymać w następujący sposób.
można otrzymać w następujący sposób.
Niech ![a/b = [c0;c1,...,ck]](/math/temat/matematyka/teoria_liczb/2018/01/25/Zlociakow_nigdy_dosyc/8x-7127b4f0c33464b38894c091d1f997ad8d62e55d-im-33,33,33-FF,FF,FF.gif) będzie takim rozwinięciem liczby
będzie takim rozwinięciem liczby 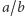 na ułamek łańcuchowy, że
na ułamek łańcuchowy, że  (takie rozwinięcie jest jedyne). Niech
(takie rozwinięcie jest jedyne). Niech ![| f/g = [c0;c1,...,ck−1].](/math/temat/matematyka/teoria_liczb/2018/01/25/Zlociakow_nigdy_dosyc/11x-7127b4f0c33464b38894c091d1f997ad8d62e55d-im-33,33,33-FF,FF,FF.gif) Wówczas
Wówczas

Teraz pojawiają się przynajmniej dwie możliwości: można próbować ją udowodnić lub obalić! Albo… rzucić się na głębszą wodę i zacząć badać pierwsze pojawienie się trójki kolejnych liczb w 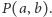 Niech
Niech 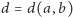 będzie taką najmniejszą liczbą
będzie taką najmniejszą liczbą 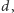 że
że 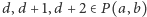 (zakładamy tu, oczywiście, że
(zakładamy tu, oczywiście, że 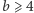 - patrz twierdzenie 1). Na drodze eksperymentów komputerowych otrzymaliśmy
- patrz twierdzenie 1). Na drodze eksperymentów komputerowych otrzymaliśmy

Niestety, nie potrafimy sformułować żadnej hipotezy dotyczącej "wzoru" na