Mała Delta
Obsesja dużych liczb
Kiedy miałem kilka, kilkanaście lat, wraz ze starszym bratem często graliśmy w grę. Należało w swojej kolejce podać liczbę większą od wskazanej przez poprzednika. Przegrywał oczywiście ten, kto nie był w stanie podać liczby większej. Czasami ponosiła nas fantazja i mówiliśmy "nieskończoność" albo "nieskończoność plus nieskończoność". Dziś już wiem, że nieskończoność liczbą nie jest, a działania na nieskończonościach są bardziej wyrafinowane, niż podejrzewałem. Gdyby i Tobie, drogi Czytelniku, przyszło kiedyś wymienić (albo usłyszeć) jakąś dużą liczbę, możesz sięgnąć do poniższej listy. Nie są to bowiem byle jakie liczby...
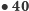 Choć znamy wiele miliardów cyfr rozwinięcia dziesiętnego liczby
Choć znamy wiele miliardów cyfr rozwinięcia dziesiętnego liczby 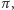 to pierwsze
to pierwsze 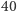 wystarcza, aby zmierzyć rozmiary znanego nam Wszechświata z dokładnością do rozmiaru atomu wodoru - najmniejszego atomu występującego w przyrodzie. Dokładność jest więc iście imponująca!
wystarcza, aby zmierzyć rozmiary znanego nam Wszechświata z dokładnością do rozmiaru atomu wodoru - najmniejszego atomu występującego w przyrodzie. Dokładność jest więc iście imponująca!

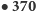 - istnieje co najmniej tyle różnych metod dowodzenia Twierdzenia Pitagorasa. Jest to rekordzista dowodowy wśród twierdzeń matematycznych.
- istnieje co najmniej tyle różnych metod dowodzenia Twierdzenia Pitagorasa. Jest to rekordzista dowodowy wśród twierdzeń matematycznych.
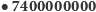 - tylu jest w przybliżeniu mieszkańców planety Ziemia. Dokładna liczba nie może być podana, gdyż, po pierwsze, nie jest znana, a po drugie, ulega częstej zmianie (statystycznie kilka razy na sekundę). Według szacunków ONZ liczba ta do końca wieku wzrośnie do około 11 miliardów.
- tylu jest w przybliżeniu mieszkańców planety Ziemia. Dokładna liczba nie może być podana, gdyż, po pierwsze, nie jest znana, a po drugie, ulega częstej zmianie (statystycznie kilka razy na sekundę). Według szacunków ONZ liczba ta do końca wieku wzrośnie do około 11 miliardów.
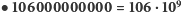 - szacunkowa liczba wszystkich ludzi, jacy kiedykolwiek żyli na Ziemi. Zaczynamy nasze obliczenia dziesiątki tysięcy lat wstecz i uwzględniamy wszystkie osoby zmarłe aż do dnia dzisiejszego - oczywiście nie zapominamy o ponad siedmiu miliardach żyjących obecnie. Zauważmy, że aktualnie żyje aż 7% wszystkich osób, jakie kiedykolwiek się urodziły.
- szacunkowa liczba wszystkich ludzi, jacy kiedykolwiek żyli na Ziemi. Zaczynamy nasze obliczenia dziesiątki tysięcy lat wstecz i uwzględniamy wszystkie osoby zmarłe aż do dnia dzisiejszego - oczywiście nie zapominamy o ponad siedmiu miliardach żyjących obecnie. Zauważmy, że aktualnie żyje aż 7% wszystkich osób, jakie kiedykolwiek się urodziły.
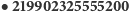 bajtów (około 200 terabajtów) - takiej mniej więcej ilości danych użyto do rozstrzygnięcia hipotezy dwukolorowalności trójek pitagorejskich. Zajęło to w sumie 35 000 godzin pracy komputerów - na szczęście pracowało nad tym wiele komputerów równocześnie. Treść problemu jest następująca: czy jest możliwe pokolorowanie każdej liczby naturalnej na czerwono lub niebiesko w taki sposób, by żadna trójka
bajtów (około 200 terabajtów) - takiej mniej więcej ilości danych użyto do rozstrzygnięcia hipotezy dwukolorowalności trójek pitagorejskich. Zajęło to w sumie 35 000 godzin pracy komputerów - na szczęście pracowało nad tym wiele komputerów równocześnie. Treść problemu jest następująca: czy jest możliwe pokolorowanie każdej liczby naturalnej na czerwono lub niebiesko w taki sposób, by żadna trójka 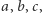 spełniająca równanie
spełniająca równanie 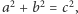 nie była jednokolorowa. Na przykład, jeżeli 5 i 12 są niebieskie, to 13 musi być czerwone. Hipoteza ta jest fałszywa, daje się we wskazany sposób pokolorować liczby naturalne od 1 do 7824 (nawet na parę sposobów), ale gdy dołączymy liczbę 7825, odpowiednie kolorowanie nie istnieje co sumiennie sprawdziły komputery.
nie była jednokolorowa. Na przykład, jeżeli 5 i 12 są niebieskie, to 13 musi być czerwone. Hipoteza ta jest fałszywa, daje się we wskazany sposób pokolorować liczby naturalne od 1 do 7824 (nawet na parę sposobów), ale gdy dołączymy liczbę 7825, odpowiednie kolorowanie nie istnieje co sumiennie sprawdziły komputery.
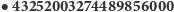 (około 43 tryliony lub
(około 43 tryliony lub 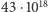 ) - to wszystkie możliwe konfiguracje elementów na kostce Rubika. Na całym świecie oryginalną kostkę oraz jej warianty sprzedano w kilkuset milionach egzemplarzy, co czyni ją najpopularniejszą zabawką w historii.
) - to wszystkie możliwe konfiguracje elementów na kostce Rubika. Na całym świecie oryginalną kostkę oraz jej warianty sprzedano w kilkuset milionach egzemplarzy, co czyni ją najpopularniejszą zabawką w historii.
Jak wyznaczyć liczbę konfiguracji? Każdy róg (element trójkolorowy) może być ustawiony w jednym z ośmiu miejsc i w jednej z trzech orientacji, co daje łącznie 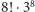 możliwości. Każda krawędź (element dwukolorowy) może być ustawiona w jednym z dwunastu miejsc i w jednej z dwóch orientacji - łącznie
możliwości. Każda krawędź (element dwukolorowy) może być ustawiona w jednym z dwunastu miejsc i w jednej z dwóch orientacji - łącznie 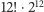 ustawień. Każdy środek (element jednokolorowy) ma stałe położenie względem ustalonej orientacji, wobec tego jest tylko jeden istotny sposób na ich ustawienie. Ostatecznie otrzymujemy liczbę
ustawień. Każdy środek (element jednokolorowy) ma stałe położenie względem ustalonej orientacji, wobec tego jest tylko jeden istotny sposób na ich ustawienie. Ostatecznie otrzymujemy liczbę 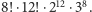 Ale nie jest to poprawna odpowiedź. Istnieją ograniczenia narzucane przez mechanizmy, które redukują liczbę dopuszczalnych możliwości.
Ale nie jest to poprawna odpowiedź. Istnieją ograniczenia narzucane przez mechanizmy, które redukują liczbę dopuszczalnych możliwości.
Ostateczna liczba zmniejsza się dwunastokrotnie, a 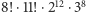 to właśnie 43 252 003 274 489 856 000.
to właśnie 43 252 003 274 489 856 000.
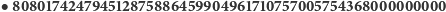 (około 808 oktyliardów lub
(około 808 oktyliardów lub 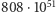 ). W XX wieku ważnym zagadnieniem w matematyce (dokładniej teorii grup) była kwestia opisania, klasyfikacji pewnych obiektów (tak zwanych skończonych grup prostych, cokolwiek to oznacza).
). W XX wieku ważnym zagadnieniem w matematyce (dokładniej teorii grup) była kwestia opisania, klasyfikacji pewnych obiektów (tak zwanych skończonych grup prostych, cokolwiek to oznacza).
Pełna klasyfikacja została osiągnięta nakładem pracy wielu matematyków oraz ponad dziesięciu tysięcy stron publikacji. Jej efektem było wyróżnienie "cegiełek", elementów, z których można zbudować wszystkie obiekty klasyfikowane. Okazało się również, że istnieje największa taka cegiełka - grupa mająca tyle elementów, ile wynosi liczba otwierająca poprzedni akapit. Grupa ta nazywa się po angielsku Monster group, co możemy dość swobodnie przetłumaczyć na grupę potworną (żartobliwie i pieszczotliwie nazywaną również potworkiem).
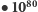 (100 tridecylionów). Szacowana liczba atomów w obserwowalnym Wszechświecie. Nie jesteśmy w stanie dokładnie ich policzyć, bazujemy jedynie na średniej gęstości materii w stosunku do znanych rozmiarów Wszechświata i na tej podstawie wyznaczamy wspomnianą liczbę. Jak ogromna jest to liczba? Przypuśćmy, że atomy ustawiliśmy w linii prostej. Każdy z nich ma średnicę około jednego nanometra (czyli
(100 tridecylionów). Szacowana liczba atomów w obserwowalnym Wszechświecie. Nie jesteśmy w stanie dokładnie ich policzyć, bazujemy jedynie na średniej gęstości materii w stosunku do znanych rozmiarów Wszechświata i na tej podstawie wyznaczamy wspomnianą liczbę. Jak ogromna jest to liczba? Przypuśćmy, że atomy ustawiliśmy w linii prostej. Każdy z nich ma średnicę około jednego nanometra (czyli 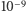 metra). Wszystkie utworzą linię długości około
metra). Wszystkie utworzą linię długości około 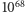 kilometrów czyli
kilometrów czyli 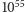 lat świetlnych.
lat świetlnych.
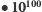 (10 seksdecyliardów lub googol) razem z
(10 seksdecyliardów lub googol) razem z 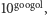 czyli googolplexem zdobyły popularność w różnych teleturniejach. W brytyjskim wydaniu "Milionerów" w pytaniu za milion funtów padło: Jak jest nazywana liczba 1 ze stoma zerami?
czyli googolplexem zdobyły popularność w różnych teleturniejach. W brytyjskim wydaniu "Milionerów" w pytaniu za milion funtów padło: Jak jest nazywana liczba 1 ze stoma zerami?
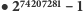 oznaczana także jako
oznaczana także jako 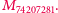 Jest największą znaną liczbą pierwszą, składa się z 22338618 cyfr. Gdybyśmy wydrukowali tę liczbę na papierze, mieszcząc 50 linii na stronie i 100 cyfr w każdej linii, zadrukowalibyśmy 4 468 stron. Taki plik kartek miałby około pół metra grubości i ważył kilka kilogramów. Papierowa wersja została zaprezentowana przez Matta Parkera na kanale YouTube "Numberphile".
Jest największą znaną liczbą pierwszą, składa się z 22338618 cyfr. Gdybyśmy wydrukowali tę liczbę na papierze, mieszcząc 50 linii na stronie i 100 cyfr w każdej linii, zadrukowalibyśmy 4 468 stron. Taki plik kartek miałby około pół metra grubości i ważył kilka kilogramów. Papierowa wersja została zaprezentowana przez Matta Parkera na kanale YouTube "Numberphile".
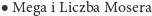 Wprowadzimy notację, pochodząca od Hugona Steinhausa, rozszerzoną później przez Leo Mosera.
Wprowadzimy notację, pochodząca od Hugona Steinhausa, rozszerzoną później przez Leo Mosera.

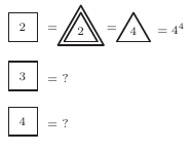
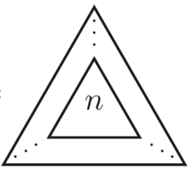
Liczba  w kwadracie oznacza liczbę
w kwadracie oznacza liczbę  w
w  zagnieżdżonych trójkątach (w wieży potęgowej jest
zagnieżdżonych trójkątach (w wieży potęgowej jest 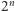 takich samych liczb). Podobnie w dalszej części mamy
takich samych liczb). Podobnie w dalszej części mamy 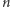 wzajemnie zagnieżdżonych kwadratów. Ogólnie można zdefiniować liczbę
wzajemnie zagnieżdżonych kwadratów. Ogólnie można zdefiniować liczbę  wpisaną w wielokąt o
wpisaną w wielokąt o 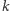 bokach jako liczbę
bokach jako liczbę 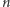 wpisaną w
wpisaną w 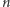 zagnieżdżonych wielokątach o
zagnieżdżonych wielokątach o 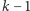 bokach.
bokach.
Steinhaus upodobał sobie szczególnie: mega - dwójka w pięciokącie - oraz megiston - dziesiątka w pięciokącie. Te dwie liczby czasami zamiast w pięciokącie zapisuje się w okręgu.
Liczba Mosera. to 2 w wielokącie, którego liczba boków jest równa liczbie mega (wielokąt taki nazywamy megagonem). Żeby móc porównać te liczby z dotychczasowymi, podamy oszacowanie (choćby grube). Jeżeli 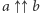 oznacza
oznacza 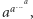 gdzie wieża potęgowa liczb
gdzie wieża potęgowa liczb 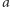 zawiera
zawiera 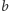 liczb, to
liczb, to

 Rozszerzamy notację strzałkową, będziemy pisali
Rozszerzamy notację strzałkową, będziemy pisali

gdzie

Niech teraz 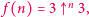 wtedy liczba Grahama zdefiniowana jest jako
wtedy liczba Grahama zdefiniowana jest jako 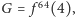 gdzie potęga przy funkcji oznacza liczbę powtórzeń. Liczba ta wystąpiła w badaniach nad uogólnionym problemem Ramseya.
gdzie potęga przy funkcji oznacza liczbę powtórzeń. Liczba ta wystąpiła w badaniach nad uogólnionym problemem Ramseya.
Ciekawostka: 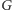 jest "znacznie" większe od liczby Mosera. Pokazano, że ta ostatnia nie jest większa od
jest "znacznie" większe od liczby Mosera. Pokazano, że ta ostatnia nie jest większa od 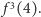
Więcej o liczbie Grahama można się dowiedzieć z artykułu Tomasza Bartnickiego Największa liczba na świecie.
Karol Gryszka
*** Posłowia ***
*** Posłowia ***
Posłowie I: Naprawdę duże liczby
Problem. Jaką największą liczbę może zwrócić program długości co najwyżej 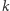 (o co najwyżej
(o co najwyżej 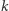 znakach)?
znakach)?
Przez 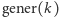 oznaczmy odpowiedź na powyższe pytanie
oznaczmy odpowiedź na powyższe pytanie 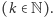 Program, który ma 100 znaków, może zwrócić liczbę zdecydowanie większą niż 100. Program złożony z 1000 znaków może zwrócić liczbę bardzo zdecydowanie większą niż 1000, ale jak bardzo zdecydowanie? Jak szybko rosną możliwości programu wraz ze wzrostem liczby jego znaków?
Program, który ma 100 znaków, może zwrócić liczbę zdecydowanie większą niż 100. Program złożony z 1000 znaków może zwrócić liczbę bardzo zdecydowanie większą niż 1000, ale jak bardzo zdecydowanie? Jak szybko rosną możliwości programu wraz ze wzrostem liczby jego znaków?
Znaków, których możemy użyć do napisania programów, jest skończenie wiele. Stąd programów o długości co najwyżej 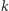 również jest skończenie wiele, a tylko niektóre z nich będą działać poprawnie i zwracać liczby. Niewątpliwie któryś z nich wygeneruje liczbę największą.
również jest skończenie wiele, a tylko niektóre z nich będą działać poprawnie i zwracać liczby. Niewątpliwie któryś z nich wygeneruje liczbę największą.
Okazuje się, że 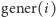 dla niedużych
dla niedużych 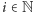 są naprawdę pokaźne, przy nich liczby Mosera lub Grahama to zupełne mikrusy. Co ciekawe, kiedy wybierzemy konkretne
są naprawdę pokaźne, przy nich liczby Mosera lub Grahama to zupełne mikrusy. Co ciekawe, kiedy wybierzemy konkretne 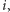 wartość
wartość 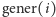 jest nieobliczalna, nie da się obliczyć jej dokładnej wartości - wyjaśnienie w tekście na sąsiedniej stronie. Można natomiast pokazać, od jakiej liczby
jest nieobliczalna, nie da się obliczyć jej dokładnej wartości - wyjaśnienie w tekście na sąsiedniej stronie. Można natomiast pokazać, od jakiej liczby 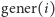 na pewno jest większe - stąd śmiałość w nazywaniu liczby Mosera mikrusem. Przyjrzyjmy się poniższemu programowi.
na pewno jest większe - stąd śmiałość w nazywaniu liczby Mosera mikrusem. Przyjrzyjmy się poniższemu programowi.

Funkcja
 zwraca liczbę
zwraca liczbę 
Przyjrzyjmy się dlaczego tak jest. Linie 4-9 rozpisują definicję notacji strzałkowej, opisanej we wcześniejszym artykule. Co się dokładniej w programie dzieje?
- Linie 2-3 - rozważamy przypadek, gdy liczba strzałek
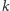 jest większa niż
jest większa niż 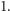 Wtedy trzeba zrobić jedną strzałkę, a potem jeszcze
Wtedy trzeba zrobić jedną strzałkę, a potem jeszcze 
- Zachodzi
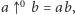 co obsługują linie
co obsługują linie 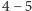 oraz
oraz 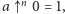 co obsługują linie
co obsługują linie 
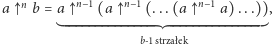 co implementują linie 8-9.
co implementują linie 8-9.
W powyższym programie, po zdefiniowaniu funkcji 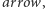 w ostatniej linii pytamy program o wartość
w ostatniej linii pytamy program o wartość 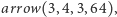 czyli o liczbę Grahama. Program ma dokładnie 201 znaków. A więc wiadomo, że
czyli o liczbę Grahama. Program ma dokładnie 201 znaków. A więc wiadomo, że 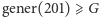 - być może istnieje program o takiej długości zwracający większą liczbę. A co powiecie o
- być może istnieje program o takiej długości zwracający większą liczbę. A co powiecie o 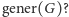
Wojciech Czerwiński
Posłowie II: Dowód nierozstrzygalności
Spróbujmy ściśle uzasadnić, że funkcja 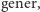 o której mowa wyżej, jest faktycznie nieobliczalna. Bardziej formalnie: chcemy udowodnić, że nie może istnieć program komputerowy
o której mowa wyżej, jest faktycznie nieobliczalna. Bardziej formalnie: chcemy udowodnić, że nie może istnieć program komputerowy 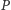 taki, który dla danej na wejściu liczby
taki, który dla danej na wejściu liczby 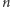 obliczy
obliczy 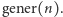
Nasze rozumowanie prowadzić będziemy nie wprost. Zakładamy więc, że jednak taki program 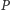 istnieje. Jego długość (okaże się bardzo ważna) oznaczmy przez
istnieje. Jego długość (okaże się bardzo ważna) oznaczmy przez 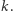 (To znaczy: kod programu
(To znaczy: kod programu 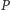 jest zapisany jako ciąg
jest zapisany jako ciąg 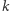 znaków.)
znaków.)
Rozważmy teraz program (a raczej szablon programu) 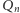 zdefiniowany następująco:
zdefiniowany następująco:
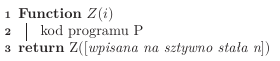
Dla jasności czym jest szablon, napiszmy kod konkretnego programu
 :
:

Programy z szablonu
 są dziwaczne: mają wbudowany program
są dziwaczne: mają wbudowany program  jako wewnętrzną funkcję
jako wewnętrzną funkcję  ; nie przyjmują żadnego wejścia oraz w swoim kodzie mają wpisaną "na sztywno" stałą
; nie przyjmują żadnego wejścia oraz w swoim kodzie mają wpisaną "na sztywno" stałą  Zastanówmy się, jaką długość ma sam program
Zastanówmy się, jaką długość ma sam program  W kod
W kod  wchodzi kod
wchodzi kod  więc tutaj zużywamy
więc tutaj zużywamy  znaków. Poza tym mamy jakąś niewielką liczbę innych znaków (jak "r", "e", "t", "u", "r", "n" itd.) oraz stałą, której zapis zużyje
znaków. Poza tym mamy jakąś niewielką liczbę innych znaków (jak "r", "e", "t", "u", "r", "n" itd.) oraz stałą, której zapis zużyje  znaków "0", "
znaków "0", "  ", "
", "  ", …, "
", …, "  ". Łącznie:
". Łącznie:  znaków dla pewnego
znaków dla pewnego 
Jak widać, program
 oblicza liczbę
oblicza liczbę  A zatem mamy, że
A zatem mamy, że  oraz, oczywiście,
oraz, oczywiście,  Jednak funkcja
Jednak funkcja  jest niemalejąca, czyli musiałoby być
jest niemalejąca, czyli musiałoby być  dla dowolnego
dla dowolnego  a to jest, oczywiście, sprzeczność dla dostatecznie dużych
a to jest, oczywiście, sprzeczność dla dostatecznie dużych 
Tomasz Kazana
Posłowie III: Ortografia
W posłowiu Wojciecha Czerwińsiego "Naprawdę duże liczby" zostało użyte następujące rozumowanie:
Skoro znaków używanych do napisania programu jest skończenie wiele i skoro program ma ograniczoną długość, to liczb definiowanych przez ten program może być też tylko skończenie wiele, a więc wśród nich musi być największa.
Powstaje pytanie, jakie dodatkowe założenia muszą zostać użyte w tym rozumowaniu, by było ono poprawne i dawało prawdziwy wniosek.
O tym, że takie pytanie ma rację bytu świadczy następujący przykład rozumowania dość podobnego do przytoczonego wyżej:
W języku polskim używamy skończonej liczby liter, więc utworzonych z nich napisów ograniczonej długości jest skończenie wiele. W szczególności skończenie wiele jest napisów używających co najwyżej stu liter. Znacznie mniej (czyli też skończenie wiele) jest wśród nich napisów sensownych, a jeszcze mniej tych, które oznaczają liczbę. Liczb dających się tak zapisać jest zatem skończenie wiele, a więc jest też największa taka liczba.
Jak to pogodzić z faktem, że napis
liczba co najmniej o jeden większa od każdej, którą można zapisać za pomocą co najwyżej stu liter
ma tylko osiemdziesiąt liter?
Owe dodatkowe założenia użyte w cytowanym tekście to reguły ortograficzne (tak, ortograficzne!), których musimy przestrzegać przy pisaniu programów.
Marek Kordos
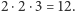
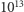 kilometrów na każdy rok. Wielkość ta nosi nazwę roku świetlnego.
kilometrów na każdy rok. Wielkość ta nosi nazwę roku świetlnego.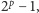 gdzie
gdzie 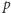 jest liczbą pierwszą, nazywamy liczbami Mersenne'a.
jest liczbą pierwszą, nazywamy liczbami Mersenne'a.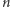 wynosi
wynosi ![[log n]+ 1. 10](/math/temat/matematyka/teoria_liczb/2017/05/28/Obsesja_duzych_liczb/2x-8e05628c6efacaca4b11e6d16b439035762d9ff9-im-33,33,33-FF,FF,FF.gif) Wyznaczmy, ile cyfr ma liczba
Wyznaczmy, ile cyfr ma liczba 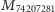 :
: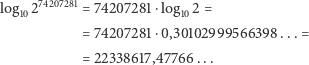
![[22338617,47766 ...]+ 1 = 22338618 cyfr](/math/temat/matematyka/teoria_liczb/2017/05/28/Obsesja_duzych_liczb/5x-8e05628c6efacaca4b11e6d16b439035762d9ff9-dm-33,33,33-FF,FF,FF.gif)
![[x]](/math/temat/matematyka/teoria_liczb/2017/05/28/Obsesja_duzych_liczb/6x-8e05628c6efacaca4b11e6d16b439035762d9ff9-im-33,33,33-FF,FF,FF.gif) oznacza część całkowitą z liczby
oznacza część całkowitą z liczby  ). Od początkowej liczby nie zostało odjęte 1, ale nie ma to wpływu na liczbę cyfr.
). Od początkowej liczby nie zostało odjęte 1, ale nie ma to wpływu na liczbę cyfr.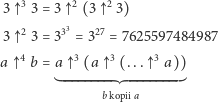
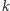 nie zwraca liczby. W takiej sytuacji ustalmy, że
nie zwraca liczby. W takiej sytuacji ustalmy, że 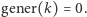 To się zdarzy tylko dla małych
To się zdarzy tylko dla małych