Drobiazgi
Małe Twierdzenie Fermata
Małe Twierdzenie Fermata ma również taki dowód...
Twierdzenie. Dla dowolnej liczby naturalnej  oraz dowolnej liczby pierwszej
oraz dowolnej liczby pierwszej 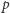 liczba
liczba 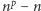 dzieli się przez
dzieli się przez 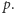
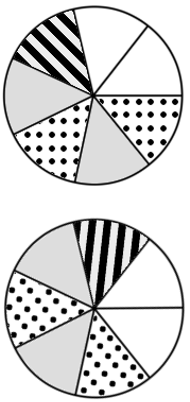
Dowód. Będziemy rozważać "koła fortuny" o 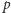 segmentach. Pytamy, ile istnieje różnych takich kół, przy założeniu, że mamy dostępne
segmentach. Pytamy, ile istnieje różnych takich kół, przy założeniu, że mamy dostępne 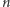 kolorów. Oczywiście, gdyby koło było nieruchome, mielibyśmy
kolorów. Oczywiście, gdyby koło było nieruchome, mielibyśmy 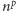 takich kół (każdy z
takich kół (każdy z 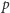 segmentów kolorujemy niezależnie na jeden z
segmentów kolorujemy niezależnie na jeden z 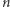 kolorów).
kolorów).
Gdy uwzględniamy możliwość obracania koła, zauważamy, że metoda podana wyżej nie może być poprawna, bo niektóre koła liczone są więcej niż raz. Konkretniej: prawidłowo (a więc jednokrotnie) liczone są tylko koła jednobarwne. Natomiast każde koło niejednobarwne liczone jest dokładnie 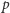 razy - każdy kolejny obrót o jeden segment daje inny obrazek (dlaczego?).
razy - każdy kolejny obrót o jeden segment daje inny obrazek (dlaczego?).
Skoro kół jednobarwnych jest 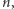 to różnych kół niejednobarwnych liczonych przy założeniu nieruchomości jest
to różnych kół niejednobarwnych liczonych przy założeniu nieruchomości jest 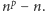 To oznacza, że różnych prawdziwych (obrotowych) niejednobarwnych kół fortuny jest dokładnie
To oznacza, że różnych prawdziwych (obrotowych) niejednobarwnych kół fortuny jest dokładnie 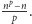 Ostatnia liczba jest, oczywiście, całkowita, a to kończy dowód tezy.
Ostatnia liczba jest, oczywiście, całkowita, a to kończy dowód tezy.
Wniosek. jeśli 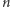 nie dzieli się przez liczbę pierwszą
nie dzieli się przez liczbę pierwszą 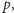 to zachodzi
to zachodzi 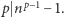
Czasem sam ten wniosek nazywa się Małym Twierdzeniem Fermata.