Rozważmy kilka pytań z teorii liczb. Cz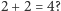y Czy 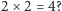Czy suma kwadratów długości przyprostokątnych w trójkącie jest równa kwadratowi długości przeciwprostokątnej? (*) Czy dla 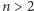równanie 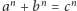ma rozwiązanie w zbiorze dodatnich liczbach naturalnych? (**) Czy każda parzysta liczba całkowita większa od dwóch jest sumą dwóch liczb pierwszych?

Żeby odpowiedzieć na powyższe pytania, zastanówmy się wpierw, czym jest liczba 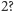Czym jest dodawanie? Czym jest trójkąt, odcinek, jego długość i jej kwadrat? Można odpowiedzieć, że to "oczywiste" lub że to "wiadomo". Jednak żeby uniknąć nieporozumień, matematycy i filozofowie w XIX wieku uznali, że matematykę należy uprawiać przez dowodzenie tez z pewników, zwanych też aksjomatami - pewnych ustalonych i znanych faktów, niebudzących żadnych wątpliwości. 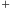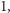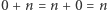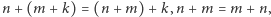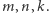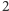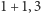Na przykład często wystarczy wiedzieć, że "liczby naturalne" (czyli nieujemne liczby całkowite) to są obiekty, na których można wykonywać dwie operacje: zwaną "dodawaniem" oraz zwaną "mnożeniem", że istnieją dwie wyróżnione liczby naturalne, oznaczone 0 oraz takie, że oraz że dla dowolnych liczb naturalnych Jeżeli zdefiniujemy jako jako 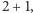i wreszcie, 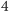jako 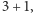to możemy w końcu udowodnić, że 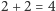: z definicji wynika, że 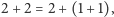a z aksjomatów wynika, że 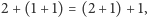i z definicji liczby 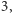jest to równe 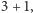co z kolei wynosi 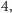na mocy definicji liczby 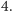Ale czy nasze aksjomaty są wystarczające, żeby dowodzić innych powszechnie znanych faktów? Np. że 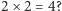Otóż nie: powyższe aksjomaty są na to zbyt słabe! Okazuje się, że możemy sobie wyobrazić inny "model" liczb niż liczby naturalne wraz z operacjami dodawania i mnożenia, które "znamy z życia". Można bowiem skonstruować zbiór 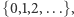zdefiniować operację 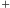jako zwykłe dodawanie, a operację zdefiniować tak, że 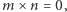dla dowolnych 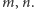Ten model będzie spełniał wszystkie aksjomaty podane powyżej. Ale jak tak można!? Przecież " " miało oznaczać mnożenie, a "wiadomo", że 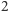pomnożone przez 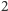daje 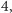a nie 0! Jednak już ustaliliśmy, że nie będziemy powoływać się na wiedzę powszechną, lecz tylko na nasze aksjomaty, a te nic takiego nie postulowały. Co więcej, nasze aksjomaty dopuszczają możliwość, że 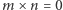dla dowolnych 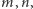ponieważ pokazaliśmy, że można skonstruować model spełniający nasze aksjomaty, oraz dodatkowo mający powyższą właściwość. A zatem nasze aksjomaty są zbyt słabe, by dowodzić niektórych powszechnie znanych faktów. Rzeczywiście, brakuje nam jeszcze kilku aksjomatów przyjmowanych przez wszystkich matematyków: np. 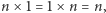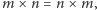że że 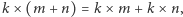że że 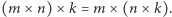Używając tych aksjomatów, możemy dowodzić więcej twierdzeń, np. że 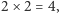ponieważ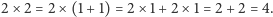

W roku 1889 Giuseppe Peano zaproponował pewien zestaw aksjomatów, nazywany teraz Aksjomatami Peano. Zawierają one wszystkie powyższe aksjomaty i parę innych prostych stwierdzeń znanych ze szkoły podstawowej, np. że 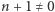dla wszystkich liczb naturalnych 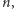oraz że jeżeli 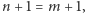to 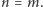Wreszcie, Aksjomaty Peano zawierają nieskończenie wiele aksjomatów, które umożliwiają przeprowadzanie dowodów przez indukcję. Mianowicie, dla każdej własności (wyrażonej w języku formalnym) jest aksjomat, który głosi, że jeżeli liczba 0 ma tę własność, oraz że z tego, iż ta własność zachodzi dla liczby 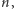wynika, że zachodzi też dla liczby 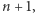to wówczas ta własność zachodzi dla wszystkich liczb naturalnych. To - z grubsza - są wszystkie Aksjomaty Peano. Co prawda jest ich nieskończenie wiele, ale są efektywne, to znaczy, że można napisać prosty program komputerowy, który będzie odpowiadał na pytanie czy dane zdanie jest jednym z Aksjomatów Peano. Inaczej mówiąc, da się je opisać w skończony sposób. Używając tych aksjomatów, z powodzeniem można dowodzić trudnych twierdzeń z teorii liczb, np. że jest nieskończenie wiele liczb pierwszych, że jest nieskończenie wiele trójek pitagorejskich (czyli takich trójek 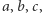że 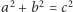), lub że każda liczba naturalna jest sumą czterech kwadratów liczb naturalnych (jest to twierdzenie Lagrange'a z roku 1770).

Pozostaje jednak pytanie: czy Aksjomaty Peano wystarczają, żeby dowodzić wszystkich prawdziwych zdań o liczbach naturalnych? To pytanie jest źle postawione: czymże bowiem są liczby naturalne? Jedyne, co możemy stwierdzić, to to, że powinny one spełniać parę oczywistych własności, takich właśnie jak te wybrane przez Peano. Moglibyśmy uznać: liczby naturalne to są właśnie takie liczby, które spełniają Aksjomaty Peano. Gdy Peano ogłosił swoje aksjomaty, wielu matematyków uznało, że jednoznacznie określają one to pojęcie, które mamy na myśli mówiąc o liczbach naturalnych. Pozostają jednak dwa problemy.

Problem 1: zupełność.

Być może Aksjomaty Peano mogą być spełnione przez "modele" mające różne własności - tak jak nasz początkowy, mały zestaw aksjomatów dopuszczał model, w którym prawdziwe było zdanie " 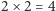" oraz inny, w którym " 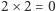". Innymi słowy, zdanie " 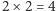" jest niezależne od owego małego zestawu aksjomatów, które dopuszczają zarówno prawdziwość tego zdania, jak i jego fałszywość. Natomiast jak widzieliśmy, Aksjomaty Peano już jednoznacznie implikują prawdziwość zdania 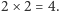Być może jednak wciąż są jakieś zdania od nich niezależne? Na przykład, czy to możliwe, że ani prawdziwość Hipotezy Goldbacha, ani jej fałszywość nie wynika z Aksjomatów Peano? W roku 1931 Kurt Gödel udowodnił, że rzeczywiście istnieją zdania niezależne od Aksjomatów Peano! Mówimy też, że Aksjomaty Peano nie są zupełne. Czyżby więc były zbyt słabe, i należy dołożyć jeszcze jakieś aksjomaty? Okazuje się, że niezupełność nie oznacza bynajmniej, że Peano zapomniał uwzględnić jakichś aksjomatów. Gödel udowodnił bowiem, że każdy efektywny (dziś powiedzielibyśmy "rozpoznawalny przez program komputerowy") zestaw aksjomatów rozszerzający Aksjomaty Peano nie będzie zupełny lub będzie sprzeczny (wyniknie z niego, że 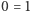)! Jest to tak zwane Pierwsze Twierdzenie Gödla o Niezupełności.

Co oznacza Pierwsze Twierdzenie o Niezupełności?

Czyżby to, że są twierdzenia matematyczne, które są prawdziwe, ale nie da się ich ani udowodnić, ani obalić? Nie! Oznacza ono jedynie tyle, że nie istnieje bezwzględne pojęcie "prawdziwego twierdzenia". Twierdzenie Gödla nie oznacza również, że są pytania matematyczne, na które odpowiedzi nigdy nie będziemy znali. Oznacza jedynie tyle, że odpowiedź na niektóre pytania nie wynika jednoznacznie z Aksjomatów Peano (i innych zestawów aksjomatów), podobnie jak odpowiedź na pytanie "ile lat ma Marek?" nie wynika z założenia, że "Marek ma jabłko". Dla każdego pytania z teorii liczb musimy więc dopuścić trzy możliwe odpowiedzi: "tak", "nie" oraz "nie wynika z Aksjomatów Peano". I tak samo każdy zestaw aksjomatów próbujący opisywać liczby naturalne, dający się opisać w skończony sposób (tzn. efektywny), nie będzie zupełny. Da się natomiast rozszerzyć Aksjomaty Peano do zupełnego zestawu aksjomatów, biorąc np. jako aksjomaty wszystkie zdania, które uznamy, że powinny zachodzić w naszych liczbach naturalnych. Możemy, na przykład, przyjąć Hipotezę Goldbacha za aksjomat, gdyż została ona potwierdzona dla wszystkich liczb mniejszych niż 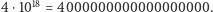Ale jeśli rozszerzymy Aksjomaty Peano o aksjomat głoszący prawdziwość tej hipotezy, to ryzykujemy, że któregoś dnia ktoś udowodni, że z Aksjomatów Peano wynika jej fałszywość, tym samym dowodząc, że nasz rozszerzony system aksjomatów jest sprzeczny. Innym problemem jest brak efektywności: nawet jeśli jakimś cudem udałoby się wybrać niesprzeczny i zupełny zestaw aksjomatów rozszerzający Aksjomaty Peano, to ten wybór będzie bardzo arbitralny: nie będzie efektywny, więc nie będzie można napisać programu komputerowego, który by rozstrzygał, czy dane zdanie jest aksjomatem, czy nie jest. A to znaczy, że matematyk nie mógłby w skończony sposób wybranych przez siebie aksjomatów opisać ani zakomunikować drugiemu matematykowi.

Problem 2: niesprzeczność.

Mało tego, że Aksjomaty Peano nie są zupełne, być może są sprzeczne! Pomimo że zostały wybrane w taki sposób, żeby nie budzić żadnych wątpliwości, tzn. wszyscy matematycy się zgadzają, że nasze wyidealizowane pojęcie o liczbach naturalnych powinno przynajmniej spełniać te aksjomaty, to wciąż jest możliwe, że któregoś dnia ktoś udowodni, że wynika z nich sprzeczność, np. że 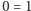(z Aksjomatów Peano wynika niewątpliwie, że 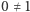). Innymi słowy, nie wiadomo, czy Aksjomaty Peano są niesprzeczne. A nawet jeżeli są, to nie da się tego udowodnić, używając samych Aksjomatów Peano! Można znowu próbować obwiniać o to Peano: dał za dużo aksjomatów, i dlatego, być może, są sprzeczne, lub dał za mało aksjomatów, i dlatego nie da się na ich podstawie udowodnić ich własnej niesprzeczności. Jednak i tym razem Peano jest tu niewinny. Gödel udowodnił bowiem, że jakiegokolwiek by nie rozważać zestawu aksjomatów, jeżeli umożliwia on rozważania arytmetyczne (tzn. dotyczące dodawania, mnożenia i ich podstawowych własności) i jest efektywny i niesprzeczny, to nie da się niesprzeczności tego zestawu udowodnić, używając tylko tych aksjomatów. Ten wynik, zwany Drugim Twierdzeniem o Niezupełności, rozszerza pierwsze Twierdzenie o Niezupełności, gdyż podaje konkretne zdanie, którego prawdziwość jest niezależna od rozważanego zestawu 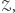mianowicie zdanie "zestaw aksjomatów 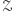jest niesprzeczny".

Czy możliwość, że Aksjomaty Peano są sprzeczne, spędza matematykom sen z oczu?

Otóż nie! Matematycy wierzą głęboko, że Aksjomaty Peano są niesprzeczne. Co więcej, potrafią to udowodnić, zakładając niesprzeczność większego zestawu aksjomatów, na przykład aksjomatów ZFC. Te aksjomaty, zamiast opisywać liczby, opisują nasze powszechne wyobrażenie na temat tego, czym są zbiory. Zaletą mówienia o zbiorach jest to, że można za ich pomocą zdefiniować zarówno liczby naturalne, dodawanie, mnożenie, jak i obiekty geometryczne, takie jak płaszczyzna, prosta, przestrzeń wielowymiarowa, a też wszystkie inne obiekty, o których na co dzień myślą matematycy. Po co nam więc Aksjomaty Peano, skoro aksjomaty ZFC dają więcej, i na dodatek dowodzą niesprzeczności Aksjomatów Peano? Otóż twierdzenia Gödla o niezupełności stosują się także do aksjomatów ZFC: z samych aksjomatów ZFC nie można udowodnić ich niesprzeczności (być może, że są sprzeczne). Można za to znaleźć kolejny zestaw aksjomatów, powiedzmy ZFCD, z którego niesprzeczności wynika niesprzeczność aksjomatów ZFC. I tak dalej. Im większe rozważamy zestawy aksjomatów, tym mniej są one uniwersalnie akceptowane przez matematyków. Gdyby ktoś udowodnił sprzeczność aksjomatów ZFCD, być może nie byłby to tak duży szok dla większości matematyków. Ale gdyby ktoś udowodnił sprzeczność aksjomatów ZFC lub samych Aksjomatów Peano, byłaby to dla matematyków prawdziwa katastrofa!

Jakie są przykłady zdań niezależnych od Aksjomatów Peano?

Jest bardzo niewiele znanych problemów z teorii liczb, o których wiadomo, że są niezależne od Aksjomatów Peano. Np. nie wiadomo, czy Wielkie Twierdzenie Fermata, które jest powszechnie uznane przez matematyków za prawdziwe, da się udowodnić, korzystając tylko z Aksjomatów Peano - dowód Andrew Wilesa, ogólnie uznawany za poprawny, używa bowiem bogatszego zbioru aksjomatów ZFC. Są też znane twierdzenia z teorii liczb, np. Twierdzenie Goodsteina, o których wiadomo, że są niezależne od Aksjomatów Peano, ale mogą być udowodnione przy użyciu aksjomatów ZFC. Z kolei wiadomo, że słynna Hipoteza Continuum jest niezależna od aksjomatów ZFC. Jednak na co dzień matematycy bardzo rzadko rozważają problemy niezależne od aksjomatów ZFC.

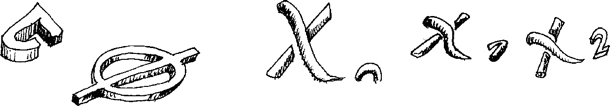
Podsumowując, nawet w matematyce niektóre fakty są przyjmowane "na wiarę", i odpowiedź na niektóre - w pełni precyzyjne - pytania może brzmieć "to zależy". Taka odpowiedź ma jednak bardzo konkretne znaczenie: oznacza, że potrafimy udowodnić, iż odpowiedź na to pytanie jest różna w różnych modelach spełniających nasze aksjomaty. Nie polecam więc wpisywać takiej odpowiedzi na egzaminie maturalnym!