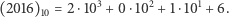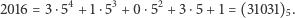Polowanie na ciągi
W 1964 roku amerykańsko-brytyjski matematyk Neil Sloane zaczął kolekcjonować znane ciągi liczb całkowitych. Niewinne hobby, motywowane zbadaniem własności kilku ciągów, które pojawiły się podczas pracy nad jego rozprawą doktorską, szybko przerodziło się w duże przedsięwzięcie. W efekcie zostały opublikowane dwie książki A Handbook of Integer Sequences (wydana w roku 1973, zawierająca 2372 ciągi) oraz The Encyclopedia of Integer Sequences (z 1995 roku, 5847 ciągi). W 1996 roku, gdy liczba zgromadzonych ciągów przekroczyła 10 000, dalsze ich przechowywanie w postaci książkowej stało się bardzo niepraktyczne...
Sloane postanowił stworzyć internetową bazę ciągów, dziś figurującą pod nazwą OEIS (The On-Line Encyclopedia of Integer Sequences). Baza zawiera obecnie około 270 000 ciągów i, aby uświadomić sobie jej wartość jako przydatnego narzędzia w pracy badawczej, wystarczy wspomnieć, że już ponad 4500 artykułów naukowych zawiera informację: Otrzymanie tego wyniku nie byłoby możliwe bez pomocy OEIS.
Znalezienie nietrywialnego ciągu liczb całkowitych, który nie figuruje na wspomnianej liście, nie jest łatwym zadaniem. W niniejszym tekście zaprezentuję, w jaki sposób udało się upolować jeden okaz. Polowanie zacznijmy od próby znalezienia odpowiedzi na właściwie błahe pytanie:
Ile jest liczb naturalnych 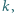 takich, że liczba
takich, że liczba 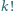 ma dokładnie
ma dokładnie 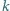 cyfr?
cyfr?
Niech 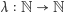 będzie funkcją określającą liczbę cyfr danej liczby (przykładowo
będzie funkcją określającą liczbę cyfr danej liczby (przykładowo 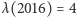 ). Powyższe pytanie możemy sformułować teraz w następujący sposób: ile rozwiązań ma równanie
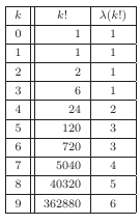
). Powyższe pytanie możemy sformułować teraz w następujący sposób: ile rozwiązań ma równanie 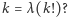 Tabela obok przedstawia wartości funkcji
Tabela obok przedstawia wartości funkcji 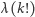 dla małych
dla małych 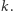
Jak widać, wśród liczb jednocyfrowych jest tylko jedno rozwiązanie (liczba 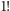 ma dokładnie jedną cyfrę). Bardzo szybki wzrost wartości funkcji
ma dokładnie jedną cyfrę). Bardzo szybki wzrost wartości funkcji 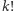 sprawia, że poszukiwanie większych rozwiązań "na piechotę" jest niezwykle nieporęczne. Z drugiej strony szybki wzrost sugeruje, że liczba rozwiązań jest skończona. Zauważmy, że liczba
sprawia, że poszukiwanie większych rozwiązań "na piechotę" jest niezwykle nieporęczne. Z drugiej strony szybki wzrost sugeruje, że liczba rozwiązań jest skończona. Zauważmy, że liczba 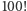 ma o dwie cyfry więcej niż
ma o dwie cyfry więcej niż 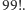 Ujmując to nieco ogólniej, jeżeli
Ujmując to nieco ogólniej, jeżeli 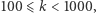 to
to

Powyższa nierówność wynika z faktu, że gdy pomnożymy dowolną liczbę przez liczbę trzycyfrową, liczba jej cyfr zwiększy się o 2 lub 3. Najmniejsze 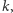 takie, że
takie, że 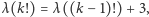 to
to 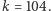
Z powyższych nierówności wynika oszacowanie:

czyli liczba 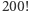 ma więcej niż 200 cyfr. Co więcej, dla każdego
ma więcej niż 200 cyfr. Co więcej, dla każdego 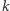 większego od 200 liczba
większego od 200 liczba 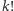 ma więcej niż
ma więcej niż 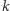 cyfr. Zatem jeżeli istnieją różne od 1 rozwiązania równania
cyfr. Zatem jeżeli istnieją różne od 1 rozwiązania równania 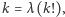 to są one na pewno mniejsze od 200.
to są one na pewno mniejsze od 200.
Problem znalezienia wszystkich rozwiązań sprowadziliśmy do zbadania liczb z zakresu od 10 do 199. Jednak przeprowadzenie bezpośrednich obliczeń wciąż byłoby całkiem czasochłonne (ze względu na bardzo duże wartości liczby 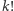 nawet dla niewielkich
nawet dla niewielkich 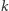 ). Znajdźmy sposób!
). Znajdźmy sposób!
Niech 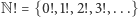 będzie zbiorem silni liczb naturalnych. Funkcja
będzie zbiorem silni liczb naturalnych. Funkcja 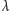 jest niemalejąca na zbiorze
jest niemalejąca na zbiorze 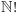 (podobnie jak na zbiorze
(podobnie jak na zbiorze 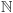 ), a po usunięciu z tego zbioru pierwszych sześciu elementów jest na nim rosnąca. Szukanie rozwiązań równania
), a po usunięciu z tego zbioru pierwszych sześciu elementów jest na nim rosnąca. Szukanie rozwiązań równania 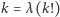 dla
dla 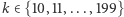 można efektywnie przeprowadzić metodą bisekcji (tj. sprawdzić, czy rozwiązaniem jest element leżący mniej więcej w środku tego zbioru, a jeśli nie, to biorąc pod uwagę wartość funkcji
można efektywnie przeprowadzić metodą bisekcji (tj. sprawdzić, czy rozwiązaniem jest element leżący mniej więcej w środku tego zbioru, a jeśli nie, to biorąc pod uwagę wartość funkcji 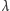 dla tego elementu, ograniczyć przeszukiwany zbiór do liczb mniejszych lub większych od tego sprawdzonego elementu).
dla tego elementu, ograniczyć przeszukiwany zbiór do liczb mniejszych lub większych od tego sprawdzonego elementu).
Przedstawmy kilka początkowych kroków zastosowania tego algorytmu. 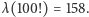 Liczba
Liczba 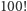 ma 158 cyfr w zapisie dziesiętnym, czyli wszystkie potencjalne rozwiązania będą znajdowały się w zbiorze
ma 158 cyfr w zapisie dziesiętnym, czyli wszystkie potencjalne rozwiązania będą znajdowały się w zbiorze 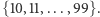
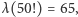 więc wszystkie potencjalne rozwiązania będą znajdowały się w zbiorze
więc wszystkie potencjalne rozwiązania będą znajdowały się w zbiorze 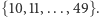 Kontynuując to rozumowanie, dochodzimy do wniosku, że jedynymi liczbami naturalnymi
Kontynuując to rozumowanie, dochodzimy do wniosku, że jedynymi liczbami naturalnymi 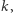 takimi, że liczba
takimi, że liczba 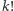 ma dokładnie
ma dokładnie 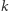 cyfr, są 1, 22, 23 i 24.
cyfr, są 1, 22, 23 i 24.
Czy to już wszystko? Czy odpowiedź na pytanie będące zalążkiem polowania jest kompletna? A co by było, gdybyśmy rozważyli liczby zapisane w innych systemach pozycyjnych?
Odpowiedź na pytanie, ile jest liczb naturalnych 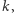 takich, że
takich, że 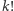 ma dokładnie
ma dokładnie 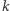 cyfr, zależy, oczywiście, od podstawy systemu pozycyjnego, w którym rozpatrujemy liczbę
cyfr, zależy, oczywiście, od podstawy systemu pozycyjnego, w którym rozpatrujemy liczbę 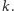 Niech
Niech 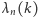 oznacza liczbę cyfr liczby
oznacza liczbę cyfr liczby 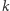 w systemie pozycyjnym o podstawie
w systemie pozycyjnym o podstawie 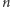 oraz niech
oraz niech 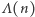 oznacza liczbę takich liczb naturalnych
oznacza liczbę takich liczb naturalnych 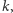 że liczba
że liczba 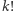 ma dokładnie
ma dokładnie 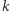 cyfr w zapisie w systemie pozycyjnym o podstawie
cyfr w zapisie w systemie pozycyjnym o podstawie 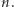 Czyli
Czyli 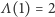 oraz
oraz 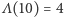 (co udowodniliśmy wcześniej).
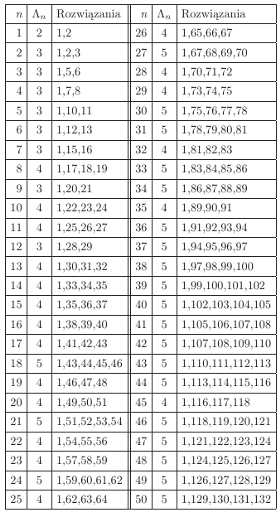
(co udowodniliśmy wcześniej). 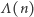 jest liczbą rozwiązań równania
jest liczbą rozwiązań równania

Przez 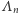 oznaczmy ciąg wartości funkcji
oznaczmy ciąg wartości funkcji 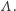 Jest to ciąg opisujący liczbę liczb
Jest to ciąg opisujący liczbę liczb 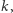 takich, że liczba
takich, że liczba 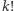 ma dokładnie
ma dokładnie 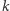 cyfr w zależności od podstawy rozpatrywanego systemu pozycyjnego. I to jest właśnie ten ciąg, który padł ofiarą naszego polowania! Teraz można pokusić się o zbadanie pewnych jego własności, co pozostawiamy jako zadanie dla Czytelnika Niezmęczonego.
cyfr w zależności od podstawy rozpatrywanego systemu pozycyjnego. I to jest właśnie ten ciąg, który padł ofiarą naszego polowania! Teraz można pokusić się o zbadanie pewnych jego własności, co pozostawiamy jako zadanie dla Czytelnika Niezmęczonego.
- Wartości ciągu
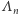 rosną bardzo powoli. Czy istnieje jakieś ograniczenie górne tego ciągu? Jeżeli tak, to jakie?
rosną bardzo powoli. Czy istnieje jakieś ograniczenie górne tego ciągu? Jeżeli tak, to jakie? - Dla jakich liczb naturalnych
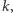 liczba
liczba 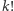 nie ma
nie ma 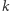 cyfr w żadnym systemie pozycyjnym?
cyfr w żadnym systemie pozycyjnym? - Tablica obok sugeruje, że wraz ze wzrostem liczby
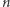 (czyli podstawy systemu pozycyjnego), wszystkie nietrywialne (różne od 1) rozwiązania równania
(czyli podstawy systemu pozycyjnego), wszystkie nietrywialne (różne od 1) rozwiązania równania 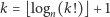
zbliżają się do liczby
 Utwierdzająca w tym przekonaniu może być tablica rozwiązań dla początkowych potęg liczby
Utwierdzająca w tym przekonaniu może być tablica rozwiązań dla początkowych potęg liczby 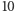 :Formalnie ten wniosek można zapisać w postaci
:Formalnie ten wniosek można zapisać w postaci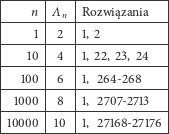
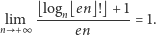
Czytelniku Poszukujący, spróbuj to udowodnić (np. stosując wzór Stirlinga).
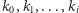 kolejnych liczb naturalnych).
kolejnych liczb naturalnych).