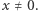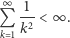Jeszcze jeden (elementarny) dowód rozbieżności szeregu odwrotności liczb pierwszych
W tym krótkim artykule autorzy chcą zaprezentować zwięzły i piękny w swej prostocie dowód rozbieżności szeregu odwrotności liczb pierwszych. Fakt ten można udowadniać, razem z innymi fundamentalnymi i bardziej wyrafinowanymi twierdzeniami teorii liczb przez cały semestr przedmiotu Teoria Liczb, na Wydziale MIM UW, ale można go również wytłumaczyć w sposób elementarny.
Udowodnimy zatem, korzystając z podstawowych zależności, następujący fakt.
Twierdzenie.
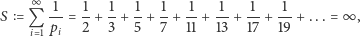 |
gdzie  to kolejne liczby pierwsze.
to kolejne liczby pierwsze.
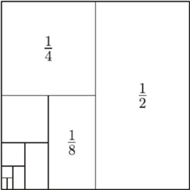
Przypomnimy, że suma nieskończonej liczby składników nie musi być nieskończona. Jeśli składniki w nieskończonej sumie są coraz mniejsze, to może ona być skończona. Jako przykład podamy standardowy szereg
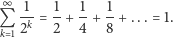 |
Tego faktu dowodzi rysunek powyżej.
Wytłumaczywszy się z tego, że nieskończenie wiele składników może sumować się do skończonej liczby, pokażemy teraz, że nawet jeśli wyrazy nieskończonej sumy są coraz mniejsze, to wcale niekoniecznie suma ta musi być skończona. Weźmy na warsztat szereg odwrotności liczb naturalnych:
Prosty dowód, pochodzący od Mikołaja Oresme, polega na "paczkowaniu" liczb naturalnych w następujący sposób.
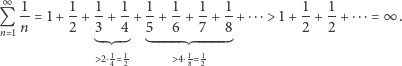 |
Każda  -ta paczka zawiera
-ta paczka zawiera 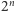 kolejnych liczb naturalnych. Suma wyrazów w paczce jest szacowana przez najmniejszy z jej wyrazów, czyli
kolejnych liczb naturalnych. Suma wyrazów w paczce jest szacowana przez najmniejszy z jej wyrazów, czyli 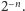 W
W  -tej paczce znajduje się ich
-tej paczce znajduje się ich 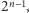 a więc
a więc  -ta paczka sumuje się do co najmniej
-ta paczka sumuje się do co najmniej 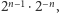 dla dowolnego numeru paczki, a paczek jest nieskończenie wiele (suma nieskończenie wielu połówek jest nieskończona).
dla dowolnego numeru paczki, a paczek jest nieskończenie wiele (suma nieskończenie wielu połówek jest nieskończona).
Lemat 2. Każdą liczbę naturalną 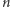 można dla pewnej naturalnej liczby
można dla pewnej naturalnej liczby 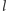 zapisać w postaci
zapisać w postaci 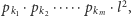 gdzie
gdzie  to liczby pierwsze.
to liczby pierwsze.
Ten fakt jest natychmiastową konsekwencją Twierdzenia o jednoznaczności rozkładu liczb naturalnych na czynniki pierwsze.
Twierdzenie (O jednoznaczności rozkładu). każdą dodatnią liczbę naturalną można zapisać w następującej postaci
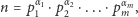 |
gdzie  są liczbami pierwszymi, a
są liczbami pierwszymi, a 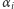 potęgami, w których występują. Rozkład ten, z dokładnością do kolejności, jest jednoznaczny.
potęgami, w których występują. Rozkład ten, z dokładnością do kolejności, jest jednoznaczny.
Dowód Lematu 2. Żeby udowodnić Lemat 2, wystarczy rozdzielić każdą liczbę pierwszą  z powyższego rozkładu, która jest podniesiona do nieparzystej potęgi,
z powyższego rozkładu, która jest podniesiona do nieparzystej potęgi, 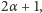 na dwa czynniki
na dwa czynniki 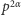 i
i 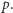 Część "parzystą" grupujemy wraz z tymi liczbami pierwszymi, które podniesione są do parzystej potęgi, w jedną liczbę
Część "parzystą" grupujemy wraz z tymi liczbami pierwszymi, które podniesione są do parzystej potęgi, w jedną liczbę 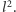 Zostają nam liczby pierwsze w potędze 1.
Zostają nam liczby pierwsze w potędze 1.

Za dowód niech wystarczy widoczny obok rysunek.
Przyda nam się jeszcze jeden pomocniczy lemat.
Mimo że znana jest dokładna suma powyższego szeregu, tutaj wystarczy fakt, że jest ona skończona.
Dowód.
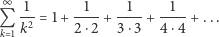 |
Zmniejszając mianownik w każdym wyrazie, dostajemy górne oszacowanie 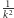 przez
przez 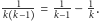 Dzięki temu prawie wszystkie wyrazy się skrócą i otrzymamy nierówność
Dzięki temu prawie wszystkie wyrazy się skrócą i otrzymamy nierówność

Dowód twierdzenia. Możemy już udowodnić twierdzenie "główne". Skorzystajmy najpierw z lematu 3. Skoro
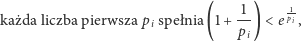 |
to można oszacować nieskończony iloczyn
 |
Oznaczmy przez 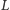 lewą stronę powyższej nierówności i wymnóżmy nawiasy:
lewą stronę powyższej nierówności i wymnóżmy nawiasy:

Przemnóżmy teraz powyższe przez skończoną sumę 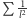 (lemat 4)
(lemat 4)
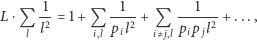 |
co wynosi dokładnie 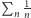 (lemat 2). Mamy zatem ostatecznie
(lemat 2). Mamy zatem ostatecznie
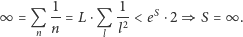 |
Dobrym zwyczajem po przeczytaniu artykułu jest samodzielne obliczenie czegoś i zastanowienie się nad podobnym problemem. Proponujemy zatem trzy pytania/zadania, o rosnącym stopniu trudności.
- 1.
- Czy suma
 jest skończona, a jeśli tak, ile wynosi?
jest skończona, a jeśli tak, ile wynosi? - 2.
- Pokazaliśmy w lemacie 4 zbieżność szeregu
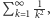 bez wskazania wyniku sumowania. Polecamy, by, inspirując się podanym dowodem, obliczyć dokładnie sumę szeregu
bez wskazania wyniku sumowania. Polecamy, by, inspirując się podanym dowodem, obliczyć dokładnie sumę szeregu 
- 3.
- Liczbami bliźniaczymi nazwiemy dwie takie liczby pierwsze, których różnica wynosi 2. Są to np. 3 i 5, 5 i 7, ..., 71 i 73, ..., 1997 i 1999. Do dziś otwarty pozostaje problem, czy liczb tych jest nieskończenie wiele (tzw. hipoteza liczb pierwszych bliźniaczych). Oczywiście, nie proponujemy Czytelnikom jako pracy domowej udowodnienia bądź obalenia hipotezy, ale sugerujemy, by zastanowić się, czy suma odwrotności wszystkich liczb pierwszych bliźniaczych jest zbieżna (czyli mniejsza niż
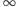 ), jeśli tak, czy można ją łatwo oszacować.
), jeśli tak, czy można ją łatwo oszacować.