Matematyka jest jedna: Magia liczb
Dotarliśmy do ostatniej części cyklu, w którym prezentujemy wybrane przykłady zaskakujących relacji pomiędzy różnymi, pozornie bardzo odległymi, obszarami matematyki. Nie wypada jednak zakończyć bez poświęcenia należytej uwagi dziedzinie teorii liczb. Jak bowiem matematyka nazywana jest często królową nauk, tak o teorii liczb mówi się często jako o królowej matematyki. A królowa ma, oczywiście, wielu służących.

Mówiąc już całkiem poważnie, proste i eleganckie w sformułowaniu problemy teorii liczb przyciągają uwagę matematyków już od tysięcy lat. Nie trzeba dodawać, iż nierzadko te pozornie proste pytania w rzeczywistości okazują się niezwykle głębokie i wymagające wielu lat wytężonej pracy tęgich umysłów matematycznych. Powstały całkiem nowe dziedziny, których rozwój był inspirowany uzyskaniem postępu w pewnych otwartych problemach teorii liczb. W ramach przykładów możemy wymienić algebraiczną teorię liczb, geometrię algebraiczną czy analityczną teorię liczb. Właśnie ta ostatnia stanowi temat przewodni artykułu.
Termin "analityczna teoria liczb" może brzmieć dosyć groźnie. I rzeczywiście - jest to trudny i zaawansowany dział matematyki, który po dziś dzień jest ciągle intensywnie rozwijany. Z góry jednak uspokajamy, że cały artykuł oparty jest na elementarnych przykładach i nie wymaga żadnej specjalistycznej wiedzy. Potrzebne będą jedynie podstawowe informacje dotyczące granic ciągów i zbieżności szeregów. W ostatnim z zadań wykorzystamy również podstawowe własności liczb zespolonych. Cała ta wiedza mieści się w programie I roku studiów i korzystając z materiałów pomocniczych, można ją w razie czego bardzo szybko uzupełnić. Okazuje się, że nawet tak podstawowe narzędzia analizy otwierają całkiem nowe możliwości w zakresie rozwiązywania problemów teorii liczb.
Metody analityczne służą często do badania teorioliczbowych własności wielomianów o współczynnikach całkowitych. Mogą być pomocne w scharakteryzowaniu wielomianów o pewnych naturalnych własnościach. Tego typu charakteryzacja stanowi treść pierwszego z zadań, pochodzącego z II etapu polskiej Olimpiady Matematycznej.
Zadanie 1. Trójmian kwadratowy 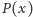 o współczynnikach całkowitych spełnia następujący warunek: dla dowolnej liczby całkowitej
o współczynnikach całkowitych spełnia następujący warunek: dla dowolnej liczby całkowitej 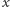 liczba
liczba 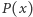 jest kwadratem liczby całkowitej. Dowieść, że wielomian
jest kwadratem liczby całkowitej. Dowieść, że wielomian 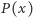 jest kwadratem pewnego wielomianu.
jest kwadratem pewnego wielomianu.
Rozwiązanie. Niech

gdzie 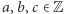 oraz
oraz 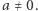 Dla dowolnej liczby naturalnej
Dla dowolnej liczby naturalnej 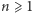 niech
niech 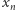 będzie taką liczbą naturalną, że
będzie taką liczbą naturalną, że 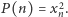 Ciąg
Ciąg 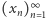 ma dwie istotne własności. Po pierwsze, jest to ciąg liczb całkowitych. Po drugie, na podstawie definicji jesteśmy w stanie określić jego tempo wzrostu. Cała sztuczka polega teraz na tym, aby z ciągiem
ma dwie istotne własności. Po pierwsze, jest to ciąg liczb całkowitych. Po drugie, na podstawie definicji jesteśmy w stanie określić jego tempo wzrostu. Cała sztuczka polega teraz na tym, aby z ciągiem 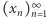 związać inny ciąg liczb całkowitych, który okaże się zbieżny. Wówczas otrzymamy naprawdę potężną dawkę informacji - zbieżny ciąg liczb całkowitych musi być przecież od pewnego miejsca stały! Jak więc znaleźć taki ciąg? Możemy myśleć w ten sposób: skoro kwadrat liczby
związać inny ciąg liczb całkowitych, który okaże się zbieżny. Wówczas otrzymamy naprawdę potężną dawkę informacji - zbieżny ciąg liczb całkowitych musi być przecież od pewnego miejsca stały! Jak więc znaleźć taki ciąg? Możemy myśleć w ten sposób: skoro kwadrat liczby 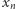 "zachowuje się" kwadratowo (jest wartością wielomianu kwadratowego), to ciąg
"zachowuje się" kwadratowo (jest wartością wielomianu kwadratowego), to ciąg 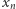 powinien "zachowywać się" liniowo. To nasuwa pomysł zbadania różnicy
powinien "zachowywać się" liniowo. To nasuwa pomysł zbadania różnicy 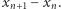 Jest to rzeczywiście dobry kierunek, gdyż możemy zauważyć, że
Jest to rzeczywiście dobry kierunek, gdyż możemy zauważyć, że

Przechodząc z 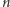 do nieskończoności, otrzymujemy
do nieskończoności, otrzymujemy

Wykazaliśmy w ten sposób, iż ciąg liczb całkowitych 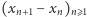 jest zbieżny. Musi być to zatem ciąg od pewnego miejsca stały i jego granica jest, oczywiście, liczbą całkowitą. Innymi słowy, istnieją takie liczby naturalne
jest zbieżny. Musi być to zatem ciąg od pewnego miejsca stały i jego granica jest, oczywiście, liczbą całkowitą. Innymi słowy, istnieją takie liczby naturalne 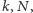 że
że 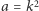 oraz
oraz 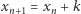 dla
dla 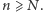 W szczególności
W szczególności

dla dowolnego  Tym samym dla dowolnego
Tym samym dla dowolnego 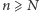 spełniona jest równość
spełniona jest równość

Ponieważ wartości wielomianów 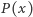 oraz
oraz 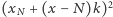 pokrywają się dla nieskończenie wielu argumentów, wielomiany te są równe. Wykazaliśmy w ten sposób, że
pokrywają się dla nieskończenie wielu argumentów, wielomiany te są równe. Wykazaliśmy w ten sposób, że 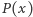 jest kwadratem pewnego wielomianu i dowód jest zakończony.
jest kwadratem pewnego wielomianu i dowód jest zakończony.
Kolejny przykład jest zaskakującym zastosowaniem słynnego faktu analizy matematycznej: szereg harmoniczny, czyli szereg 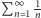 kolejnych odwrotności liczb naturalnych, jest rozbieżny.
kolejnych odwrotności liczb naturalnych, jest rozbieżny.
Zadanie 2. Dane są liczby całkowite 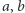 większe od
większe od 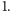 Udowodnić, że istnieje pewna wielokrotność liczby
Udowodnić, że istnieje pewna wielokrotność liczby 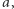 która zapisana w systemie pozycyjnym o podstawie
która zapisana w systemie pozycyjnym o podstawie 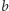 zawiera każdą z cyfr
zawiera każdą z cyfr 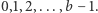
Rozwiązanie. Rozwiązanie będzie przebiegać w sposób niekonstruktywny. Zamiast wskazywać konkretną wielokrotność liczby  która ma żądaną własność, założymy, że teza zadania nie jest prawdziwa i dojdziemy do sprzeczności. Ponieważ szereg harmoniczny
która ma żądaną własność, założymy, że teza zadania nie jest prawdziwa i dojdziemy do sprzeczności. Ponieważ szereg harmoniczny  odwrotności kolejnych liczb naturalnych jest rozbieżny, rozbieżny jest również szereg
odwrotności kolejnych liczb naturalnych jest rozbieżny, rozbieżny jest również szereg 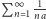 odwrotności wielokrotności liczby
odwrotności wielokrotności liczby  Niech
Niech  oznacza zbiór liczb naturalnych
oznacza zbiór liczb naturalnych 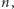 które w zapisie pozycyjnym o podstawie
które w zapisie pozycyjnym o podstawie 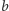 nie zawierają choćby jednej z
nie zawierają choćby jednej z 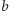 możliwych cyfr. Jeżeli teza zadania nie jest prawdziwa, to zbiór
możliwych cyfr. Jeżeli teza zadania nie jest prawdziwa, to zbiór 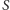 zawiera wszystkie wielokrotności liczby
zawiera wszystkie wielokrotności liczby 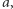 a więc w szczególności szereg
a więc w szczególności szereg 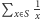 jest rozbieżny. Udowodnimy, że ten szereg jest zbieżny, uzyskując w ten sposób sprzeczność, która w efekcie zakończy rozwiązanie zadania.
jest rozbieżny. Udowodnimy, że ten szereg jest zbieżny, uzyskując w ten sposób sprzeczność, która w efekcie zakończy rozwiązanie zadania.
Ustalmy dowolną cyfrę ze zbioru 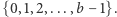 Łatwo zauważyć, że wystarczy udowodnić, iż szereg odwrotności tych liczb, które nie zawierają w swoim zapisie właśnie tej ustalonej cyfry, jest zbieżny. Zauważmy dalej, że liczb o
Łatwo zauważyć, że wystarczy udowodnić, iż szereg odwrotności tych liczb, które nie zawierają w swoim zapisie właśnie tej ustalonej cyfry, jest zbieżny. Zauważmy dalej, że liczb o  cyfrach w zapisie o podstawie
cyfrach w zapisie o podstawie 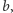 które nie zawierają pewnej ustalonej cyfry, jest co najwyżej
które nie zawierają pewnej ustalonej cyfry, jest co najwyżej  - bowiem każdą z cyfr możemy wybrać na co najwyżej
- bowiem każdą z cyfr możemy wybrać na co najwyżej 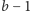 sposobów. Co więcej, liczba o
sposobów. Co więcej, liczba o  cyfrach jest nie mniejsza niż
cyfrach jest nie mniejsza niż 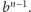 Jej odwrotność nie przekracza więc
Jej odwrotność nie przekracza więc 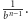 Ponieważ liczb
Ponieważ liczb  -cyfrowych niezawierających ustalonej cyfry jest co najwyżej
-cyfrowych niezawierających ustalonej cyfry jest co najwyżej 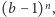 ich suma odwrotności jest zatem nie większa niż
ich suma odwrotności jest zatem nie większa niż 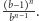 Sumując po wszystkich
Sumując po wszystkich 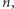 otrzymujemy, iż szereg odwrotności liczb naturalnych, które nie zawierają pewnej ustalonej cyfry, nie przekracza
otrzymujemy, iż szereg odwrotności liczb naturalnych, które nie zawierają pewnej ustalonej cyfry, nie przekracza

gdzie ostatnia z równości wynika bezpośrednio ze wzoru na sumę szeregu geometrycznego. Powyższy szereg jest więc zbieżny i dowód jest zakończony.
Kolejne zadanie dotyczy klasycznego twierdzenia Schura o wielomianach o współczynnikach całkowitych.
Zadanie 3 (Twierdzenie Schura). Dany jest niestały wielomian 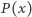 o współczynnikach całkowitych. Udowodnić, że dla nieskończenie wielu liczb pierwszych
o współczynnikach całkowitych. Udowodnić, że dla nieskończenie wielu liczb pierwszych 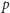 istnieje taka liczba naturalna
istnieje taka liczba naturalna 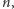 że
że 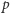 dzieli
dzieli 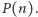
Rozwiązanie. Dla dowodu nie wprost załóżmy, że istnieje jedynie skończenie wiele liczb pierwszych 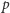 o takiej własności. Niech będą to liczby
o takiej własności. Niech będą to liczby 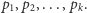 Wówczas dla dowolnego
Wówczas dla dowolnego 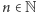 w rozkładzie na czynniki pierwsze liczby
w rozkładzie na czynniki pierwsze liczby  pojawiają się tylko pewne z liczb
pojawiają się tylko pewne z liczb 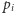 dla
dla 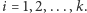 Innymi słowy,
Innymi słowy, 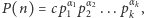 gdzie
gdzie  są nieujemnymi liczbami całkowitymi oraz
są nieujemnymi liczbami całkowitymi oraz 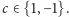
Ustalmy liczbę rzeczywistą 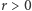 i zauważmy, że
i zauważmy, że

przy czym sumowanie odbywa się po całkowitych 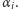 Pierwsza z równości wynika z bezpośredniego wymnożenia wszystkich nawiasów i z jednoznaczności rozkładu na czynniki pierwsze - liczba
Pierwsza z równości wynika z bezpośredniego wymnożenia wszystkich nawiasów i z jednoznaczności rozkładu na czynniki pierwsze - liczba 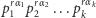 pojawi się tylko jako efekt wymnożenia
pojawi się tylko jako efekt wymnożenia  -go składnika z
-go składnika z 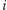 -go czynnika iloczynu. Druga z równości to, oczywiście, bezpośrednie zastosowanie wzoru na sumę szeregu geometrycznego. Widzimy więc w szczególności, że szereg
-go czynnika iloczynu. Druga z równości to, oczywiście, bezpośrednie zastosowanie wzoru na sumę szeregu geometrycznego. Widzimy więc w szczególności, że szereg

jest zbieżny dla dowolnej liczby rzeczywistej 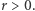
Niech zatem 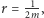 gdzie
gdzie  jest stopniem wielomianu
jest stopniem wielomianu 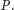 Dla odpowiednio dużych
Dla odpowiednio dużych 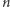 prawdziwa jest wówczas nierówność
prawdziwa jest wówczas nierówność

gdyż po podniesieniu obu stron nierówności do potęgi 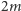 sprowadza się ona do
sprowadza się ona do 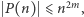 a wielomian
a wielomian 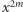 jest wielomianem wyższego stopnia niż
jest wielomianem wyższego stopnia niż 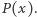 W szczególności
W szczególności

Z drugiej jednak strony każda liczba 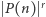 jest postaci
jest postaci 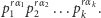 Co więcej, dowolna liczba postaci
Co więcej, dowolna liczba postaci 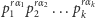 jest równa co najwyżej
jest równa co najwyżej 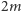 liczbom
liczbom  - wielomian
- wielomian 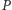 nie jest stały, a więc każdą wartość przyjmuje co najwyżej
nie jest stały, a więc każdą wartość przyjmuje co najwyżej  razy, tak samo jak wielomian
razy, tak samo jak wielomian 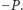 A zatem
A zatem

Otrzymana sprzeczność kończy dowód.
Istnieje wiele dowodów twierdzenia Schura. Zachęcamy gorąco Czytelnika do próby odnalezienia innego - dowód zaprezentowany powyżej jest bardzo niecodzienny, ale da się przeprowadzić bardziej nasuwające się rozumowanie, które prowadzi do konkluzji twierdzenia. Powyższy dowód ma jednak istotną zaletę: w rzeczywistości wynika z niego znacznie więcej. Zauważmy bowiem, że dla dowolnego ciągu liczb całkowitych dodatnich  można zapytać o to, czy istnieje nieskończenie wiele liczb pierwszych
można zapytać o to, czy istnieje nieskończenie wiele liczb pierwszych 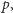 takich, że
takich, że 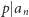 dla pewnego
dla pewnego 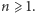 Nie jest tak, oczywiście, dla każdego ciągu: wystarczy wziąć ciąg stały albo ciąg
Nie jest tak, oczywiście, dla każdego ciągu: wystarczy wziąć ciąg stały albo ciąg 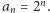 Jeżeli jednak założymy dodatkowo, że istnieje taka liczba naturalna
Jeżeli jednak założymy dodatkowo, że istnieje taka liczba naturalna 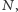 że każda liczba naturalna jest wartością ciągu
że każda liczba naturalna jest wartością ciągu 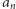 dla co najwyżej
dla co najwyżej 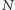 indeksów
indeksów 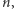 oraz że wyrazy ciągu rosną w tempie nie szybszym niż wielomianowym - czyli, że istnieje taki wielomian
oraz że wyrazy ciągu rosną w tempie nie szybszym niż wielomianowym - czyli, że istnieje taki wielomian 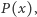 że
że 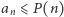 dla odpowiednio dużych
dla odpowiednio dużych 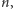 to powyższe rozumowanie gwarantuje nieskończony zbiór liczb pierwszych, z których każda dzieli pewien wyraz ciągu. Przedstawiony argument daje więc pozytywną odpowiedź w bardzo szerokiej klasie ciągów.
to powyższe rozumowanie gwarantuje nieskończony zbiór liczb pierwszych, z których każda dzieli pewien wyraz ciągu. Przedstawiony argument daje więc pozytywną odpowiedź w bardzo szerokiej klasie ciągów.
Ostatnie z zadań należy do podobnej kategorii co zadanie pierwsze. Dotyczy ono charakteryzacji unormowanych wielomianów o współczynnikach całkowitych, które osiągają każdą z potęg liczby 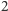 dla argumentów całkowitych. Główny pomysł rozwiązania również jest zbliżony, lecz zrealizowanie go w szczegółach wymaga większego zaangażowania.
dla argumentów całkowitych. Główny pomysł rozwiązania również jest zbliżony, lecz zrealizowanie go w szczegółach wymaga większego zaangażowania.
Zadanie 4. Dany jest unormowany wielomian 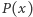 o współczynnikach całkowitych, który spełnia następujący warunek: dla dowolnej liczby całkowitej dodatniej
o współczynnikach całkowitych, który spełnia następujący warunek: dla dowolnej liczby całkowitej dodatniej  istnieje taka liczba całkowita dodatnia
istnieje taka liczba całkowita dodatnia 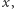 że
że 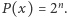 Udowodnić, że wielomian
Udowodnić, że wielomian  jest wielomianem liniowym.
jest wielomianem liniowym.
Rozwiązanie. Oznaczmy przez 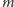 stopień wielomianu
stopień wielomianu  Naszym celem jest wykazanie równości
Naszym celem jest wykazanie równości 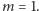 Z treści zadania wynika, że dla dowolnej liczby całkowitej
Z treści zadania wynika, że dla dowolnej liczby całkowitej 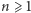 istnieje taka liczba całkowita
istnieje taka liczba całkowita 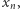 że
że 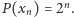 Podobnie jak w zadaniu pierwszym, możemy próbować wykorzystać ten warunek, aby związać z ciągiem
Podobnie jak w zadaniu pierwszym, możemy próbować wykorzystać ten warunek, aby związać z ciągiem 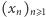 inny ciąg liczb całkowitych, który okaże się zbieżny, a więc od pewnego miejsca stały. Przeprowadzimy najpierw czysto heurystyczne rozumowanie, które pomoże nam znaleźć kandydata na tego typu ciąg. Ponieważ wielomian
inny ciąg liczb całkowitych, który okaże się zbieżny, a więc od pewnego miejsca stały. Przeprowadzimy najpierw czysto heurystyczne rozumowanie, które pomoże nam znaleźć kandydata na tego typu ciąg. Ponieważ wielomian 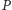 jest unormowany i stopnia
jest unormowany i stopnia  możemy myśleć, że dla dużych wartości
możemy myśleć, że dla dużych wartości  wartość
wartość 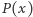 "zachowuje się" jak
"zachowuje się" jak 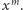 Skoro tak, to aby zachodziła równość
Skoro tak, to aby zachodziła równość 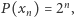 wyraz
wyraz  powinien "zachowywać się" jak
powinien "zachowywać się" jak  Zauważmy jednak, że
Zauważmy jednak, że 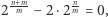 co sugeruje, że dobrym kandydatem może być ciąg
co sugeruje, że dobrym kandydatem może być ciąg 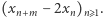 Okazuje się, że tak jest w istocie - udowodnimy, że jest to ciąg zbieżny.
Okazuje się, że tak jest w istocie - udowodnimy, że jest to ciąg zbieżny.
W pierwszej kolejności dowiedziemy nieco słabszej własności: 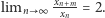 Zauważmy najpierw, że ciąg
Zauważmy najpierw, że ciąg 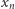 dąży, oczywiście, do nieskończoności. Ponieważ współczynnik w
dąży, oczywiście, do nieskończoności. Ponieważ współczynnik w 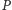 przy
przy  jest równy
jest równy  to dostajemy
to dostajemy  Tym samym
Tym samym

a stąd, oczywiście, mamy 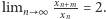 Ciąg
Ciąg 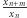 niekoniecznie jest ciągiem liczb całkowitych, a więc jego zbieżność nie daje jeszcze nam bezpośrednio istotnych korzyści. Jest to jednak pomocny krok pośredni.
niekoniecznie jest ciągiem liczb całkowitych, a więc jego zbieżność nie daje jeszcze nam bezpośrednio istotnych korzyści. Jest to jednak pomocny krok pośredni.
Zapiszmy bowiem wielomian 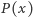 w postaci
w postaci

dla pewnych liczb całkowitych 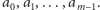 Z równości
Z równości 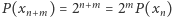 otrzymujemy
otrzymujemy

Ze wzoru na różnicę 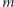 -tych potęg mamy ponadto
-tych potęg mamy ponadto

co w połączeniu daje nam zależność

Przechodząc z  do nieskończoności w powyższej równości i korzystając z wcześniej udowodnionego faktu
do nieskończoności w powyższej równości i korzystając z wcześniej udowodnionego faktu 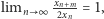 otrzymujemy zatem zbieżność ciągu
otrzymujemy zatem zbieżność ciągu 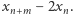 Jest to ciąg liczb całkowitych, a więc istnieje liczba naturalna
Jest to ciąg liczb całkowitych, a więc istnieje liczba naturalna 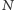 oraz liczba całkowita
oraz liczba całkowita 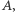 dla których
dla których 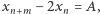 gdy
gdy 
Wykazaliśmy w ten sposób, że dla odpowiednio dużych 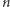 prawdziwa jest równość
prawdziwa jest równość 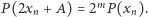 To jednak oznacza, iż wielomian
To jednak oznacza, iż wielomian 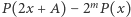 ma nieskończenie wiele pierwiastków, a więc jest wielomianem zerowym. Czyli dla dowolnej liczby rzeczywistej
ma nieskończenie wiele pierwiastków, a więc jest wielomianem zerowym. Czyli dla dowolnej liczby rzeczywistej 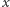 prawdziwa jest równość
prawdziwa jest równość 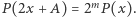
Wychodząc od teorioliczbowego warunku danego w treści zadania, udało nam się zatem dotrzeć do czysto algebraicznej zależności, którą spełnia wielomian  Aby doprowadzić rozwiązanie do końca, posłużymy się liczbami zespolonymi. Jak wiadomo, każdy wielomian ma tyle pierwiastków zespolonych, ile wynosi jego stopień. Niech
Aby doprowadzić rozwiązanie do końca, posłużymy się liczbami zespolonymi. Jak wiadomo, każdy wielomian ma tyle pierwiastków zespolonych, ile wynosi jego stopień. Niech 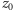 będzie zatem dowolnym zespolonym pierwiastkiem wielomianu
będzie zatem dowolnym zespolonym pierwiastkiem wielomianu 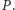 Wówczas
Wówczas

skąd wynika, że  jest również pierwiastkiem wielomianu
jest również pierwiastkiem wielomianu 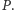 Kontynuując w ten sposób, widzimy, że pierwiastkiem wielomianu
Kontynuując w ten sposób, widzimy, że pierwiastkiem wielomianu 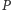 są również liczby
są również liczby  Wielomian
Wielomian 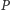 nie jest jednak wielomianem zerowym, a więc liczby w tym ciągu muszą od pewnego miejsca zacząć się powtarzać. To zaś oznacza, że dla pewnych liczb naturalnych
nie jest jednak wielomianem zerowym, a więc liczby w tym ciągu muszą od pewnego miejsca zacząć się powtarzać. To zaś oznacza, że dla pewnych liczb naturalnych 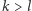 mamy
mamy

co z kolei można przekształcić do postaci

a stąd, oczywiście, 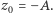
Dowiedliśmy zatem, iż każdy pierwiastek wielomianu 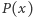 jest równy
jest równy 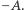 Skoro wielomian
Skoro wielomian 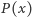 jest unormowany, to w takim razie
jest unormowany, to w takim razie 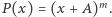 W tym momencie teza zadania staje się ewidentna:
W tym momencie teza zadania staje się ewidentna:

Liczba 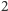 jest
jest  -tą potęga liczby całkowitej tylko dla
-tą potęga liczby całkowitej tylko dla 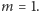 Wielomian
Wielomian 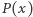 jest więc wielomianem liniowym i rozwiązanie jest zakończone.
jest więc wielomianem liniowym i rozwiązanie jest zakończone.
W ten sposób dotarliśmy do końca cyklu. Żywimy nadzieję, że ukazał on korzyści płynące z zachowania otwartości umysłu na niecodzienne pomysły. Podobnie jak odwagi do podążania niekoniecznie najbardziej narzucającą się drogą. Któż bowiem wie, co ciekawego może nas na niej spotkać?
Metody, które Czytelnik miał okazję spotkać w powyższych przykładach, może wykorzystać w dwóch zadaniach do samodzielnego rozwiązania.
Metody, które Czytelnik miał okazję spotkać w powyższych przykładach, może wykorzystać w dwóch zadaniach do samodzielnego rozwiązania.
Zadanie 5. Liczby całkowite  i
i 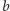 spełniają następujący warunek: dla dowolnej liczby całkowitej dodatniej
spełniają następujący warunek: dla dowolnej liczby całkowitej dodatniej 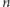 liczba
liczba  jest kwadratem liczby całkowitej. Udowodnić, że
jest kwadratem liczby całkowitej. Udowodnić, że 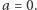
Podpowiedź. Niech 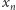 będzie taką liczbą całkowitą dodatnią, że
będzie taką liczbą całkowitą dodatnią, że 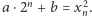 Rozważ ciąg
Rozważ ciąg 
Zadanie 6. Dany jest rosnący ciąg 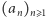 liczb całkowitych, który spełnia warunek
liczb całkowitych, który spełnia warunek 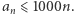 Wykazać, że w ciągu istnieje nieskończenie wiele wyrazów, które w zapisie dziesiętnym mają co najmniej
Wykazać, że w ciągu istnieje nieskończenie wiele wyrazów, które w zapisie dziesiętnym mają co najmniej 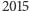 kolejnych cyfr równych 1.
kolejnych cyfr równych 1.
Podpowiedź. Niech 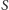 będzie zbiorem liczb, które w zapisie dziesiętnym nie mają ciągu
będzie zbiorem liczb, które w zapisie dziesiętnym nie mają ciągu  kolejnych cyfr równych
kolejnych cyfr równych 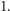 Udowodnij, że szereg
Udowodnij, że szereg  jest zbieżny. Oszacuj w tym celu od góry liczbę liczb
jest zbieżny. Oszacuj w tym celu od góry liczbę liczb  cyfrowych w zbiorze
cyfrowych w zbiorze