O pewnym uogólnieniu małego twierdzenia Fermata
Udowodnione ponad trzysta lat temu małe twierdzenie Fermata głosi, że dla każdej liczby całkowitej  i liczby pierwszej
i liczby pierwszej 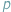 zachodzi podzielność
zachodzi podzielność 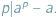 Pragnę przedstawić jego uogólnienie, związane z iteracją funkcji zespolonej
Pragnę przedstawić jego uogólnienie, związane z iteracją funkcji zespolonej 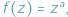 gdzie
gdzie  jest liczbą całkowitą.
jest liczbą całkowitą.
Część wstępna
Niech 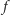 będzie funkcją określoną na pewnym niepustym zbiorze
będzie funkcją określoną na pewnym niepustym zbiorze  przyjmującą wartości w tym zbiorze. Przyjmijmy oznaczenie
przyjmującą wartości w tym zbiorze. Przyjmijmy oznaczenie  (tzn.
(tzn. 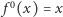 dla każdego
dla każdego 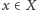 ) oraz w sposób indukcyjny zdefiniujmy
) oraz w sposób indukcyjny zdefiniujmy  dla dodatnich liczb naturalnych
dla dodatnich liczb naturalnych 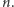
Powiemy, że 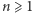 jest okresem punktu
jest okresem punktu 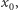 jeżeli
jeżeli 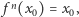 natomiast okresem podstawowym punktu
natomiast okresem podstawowym punktu 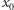 nazwiemy najmniejszy spośród jego okresów (o ile takie istnieją). Zauważmy, że
nazwiemy najmniejszy spośród jego okresów (o ile takie istnieją). Zauważmy, że
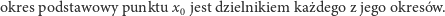 |
(*) |
Rzeczywiście, niech  będzie okresem podstawowym, a
będzie okresem podstawowym, a 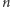 pewnym okresem
pewnym okresem 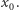 Niech
Niech 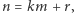 gdzie
gdzie  jest resztą z dzielenia
jest resztą z dzielenia 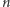 przez
przez 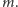 Przypuśćmy, że
Przypuśćmy, że  Wtedy
Wtedy

co jest sprzeczne z definicją liczby 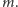
Załóżmy, że dla dowolnej liczby naturalnej 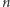 funkcja
funkcja 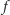 ma skończenie wiele punktów o okresie
ma skończenie wiele punktów o okresie 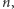 a ich liczbę oznaczmy przez
a ich liczbę oznaczmy przez 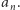 Ponadto niech
Ponadto niech  będzie liczbą punktów o okresie podstawowym
będzie liczbą punktów o okresie podstawowym  Wówczas z
Wówczas z  łatwo wynika
łatwo wynika

Rozważmy teraz 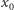 o okresie podstawowym
o okresie podstawowym 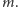 Wówczas
Wówczas 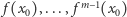 również mają okres podstawowy
również mają okres podstawowy  W przeciwnym razie,
W przeciwnym razie, 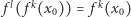 dla pewnego
dla pewnego 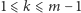 i
i 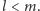 Stąd
Stąd  więc
więc

co prowadzi do sprzeczności, ponieważ 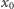 ma okres minimalny
ma okres minimalny  i
i 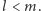 Ponadto punkty
Ponadto punkty  są parami różne, gdyż gdyby
są parami różne, gdyż gdyby 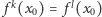 dla pewnych
dla pewnych 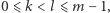 to
to

czyli 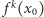 miałby okres minimalny nie większy niż
miałby okres minimalny nie większy niż 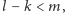 co (jak pokazaliśmy wcześniej) jest niemożliwe. Z poczynionych obserwacji wynika, że zbiór punktów o okresie podstawowym
co (jak pokazaliśmy wcześniej) jest niemożliwe. Z poczynionych obserwacji wynika, że zbiór punktów o okresie podstawowym  jest sumą skończonej liczby rozłącznych,
jest sumą skończonej liczby rozłącznych, 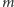 -elementowych zbiorów postaci
-elementowych zbiorów postaci 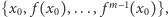 a zatem
a zatem 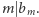
Zauważmy teraz, że jeżeli 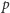 jest liczbą pierwszą, to
jest liczbą pierwszą, to  zatem
zatem  Analogicznie, jeśli
Analogicznie, jeśli 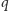 jest liczbą pierwszą różną od
jest liczbą pierwszą różną od  to wówczas
to wówczas 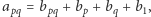 a skoro
a skoro  więc
więc

Okazuje się, że otrzymywane równości możemy uogólnić, korzystając z formuły inwersyjnej Möbiusa, wedle której jeśli 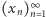 i
i 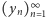 są ciągami liczb całkowitych oraz
są ciągami liczb całkowitych oraz 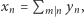 to wówczas
to wówczas 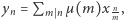 gdzie
gdzie

Jej bezpośrednie zastosowanie prowadzi nas do równości 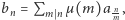 co w połączeniu z podzielnością
co w połączeniu z podzielnością 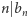 pozwala stwierdzić, że dla dowolnej liczby naturalnej
pozwala stwierdzić, że dla dowolnej liczby naturalnej 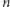

Część zasadnicza

Wróćmy do twierdzenia Fermata.
Dla ustalonego 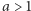 rozważmy funkcję zespoloną
rozważmy funkcję zespoloną 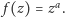 Złożenie
Złożenie 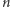 -krotne funkcji
-krotne funkcji 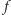 jest równe
jest równe

Zauważmy, że dla każdego  zbiór wszystkich punktów okresowych o okresie
zbiór wszystkich punktów okresowych o okresie  jest skończony. Rzeczywiście, składa się on z zespolonych pierwiastków równania
jest skończony. Rzeczywiście, składa się on z zespolonych pierwiastków równania

Jednym z jego pierwiastków jest  a jeżeli
a jeżeli 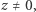 to
to 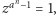 więc
więc  jest pierwiastkiem zespolonym z jedynki stopnia
jest pierwiastkiem zespolonym z jedynki stopnia  a tych jest dokładnie
a tych jest dokładnie  Wynika stąd, że w tej sytuacji
Wynika stąd, że w tej sytuacji

Dla liczby pierwszej 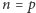 otrzymujemy małe twierdzenie Fermata:
otrzymujemy małe twierdzenie Fermata: 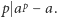
Czytelnik Uważny zauważy, że dla 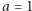 nie możemy stosować naszego rozumowania (dlaczego?). Na szczęście zachodzi
nie możemy stosować naszego rozumowania (dlaczego?). Na szczęście zachodzi 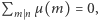 dla dowolnej liczby naturalnej
dla dowolnej liczby naturalnej  zatem nasze twierdzenie pozostaje prawdziwe i w tym przypadku.
zatem nasze twierdzenie pozostaje prawdziwe i w tym przypadku.
Spróbujmy pójść jeszcze krok dalej. Niech 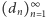 będzie ciągiem liczb całkowitych. Powiemy, że jest on ciągiem Dolda, jeżeli dla każdej liczby naturalnej zachodzi podzielność
będzie ciągiem liczb całkowitych. Powiemy, że jest on ciągiem Dolda, jeżeli dla każdej liczby naturalnej zachodzi podzielność

Z wcześniejszych rozważań wynika, że ciąg 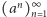 jest ciągiem Dolda dla dowolnej liczby całkowitej
jest ciągiem Dolda dla dowolnej liczby całkowitej 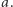
Ciągi Dolda mają ciekawą charakteryzację. Niech 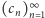 będzie ciągiem liczb całkowitych. Powiemy, że ciąg
będzie ciągiem liczb całkowitych. Powiemy, że ciąg 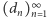 jest generowany przez ciąg
jest generowany przez ciąg 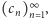 jeżeli dla
jeżeli dla 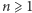 zachodzi
zachodzi

Okazuje się, że 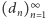 jest ciągiem Dolda wtedy i tylko wtedy, gdy jest generowany przez pewien ciąg
jest ciągiem Dolda wtedy i tylko wtedy, gdy jest generowany przez pewien ciąg 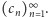 Zostało to wykazane przez Bau-Sen Du, Sen-Shan Huanga i Ming-Chia Li - ich dowód można znaleźć w artykule Generalized Fermat, double Fermat and Newton sequences opublikowanym w czasopiśmie Journal of Number Theory w 2003 roku.
Zostało to wykazane przez Bau-Sen Du, Sen-Shan Huanga i Ming-Chia Li - ich dowód można znaleźć w artykule Generalized Fermat, double Fermat and Newton sequences opublikowanym w czasopiśmie Journal of Number Theory w 2003 roku.