Drobiazgi

Dwa zadania

Zadanie 1. Znaleźć regułę, według której skonstruowany jest ciąg o 30 początkowych wyrazach podanych obok.

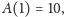
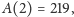
Rozwiązanie 1. 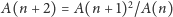$\text{[math]}$ $\text{[math]}$ $\text{[math]}$ zaokrąglone do najbliższej liczby całkowitej. To znaczy: zaczynamy od 10 i 219, za każdym razem wybieramy liczbę, która z najlepszym przybliżeniem tworzy ciąg geometryczny z poprzednimi dwiema.

Rozwiązanie 2. Zaczynamy od 10, 219, 4796, 105030 i kontynuujemy według wzoru

$pict$

(rekursja liniowa 4. rzędu).

Zadanie 2. Skoro dany ciąg może być zdefiniowany na dwa różne sposoby, to jak wykazać, że te dwie definicje są równoważne?

Rozwiązanie. No cóż, można obliczyć pierwszych 1000 wyrazów, używając obu definicji, i przekonać się, że wszystko się zgadza. Wydrukowanie tysiąca początkowych wyrazów zajęłoby pokaźnych rozmiarów książkę. Czyż trzeba bardziej przekonującego argumentu? Tak, trzeba. Tylko że takiego argumentu po prostu nie ma. Obie, bądź co bądź, bardzo proste definicje określają dwa różne ciągi!!! Jedynie „skromny” początek obu ciągów, składający się z 1402 wyrazów, jest taki sam. Ale według pierwszej definicji 1403. wyraz jest równy
1943708471314943308059445452657010940487450311864066842732596790939279068
191168021439671095304800683519756645143142801766345115405789059172602192
426024357604507643919310528104572431148473422703387902120314696316682603
735267692111685622339243356242260056059336217912799059786079481997806631
913955493134941095358770263918313025848373581726054928149011342047774528
154248287433782463237576416857026309254788755903742777139477594456385042
020381315538604379941789590322666368814892780385046811477655985825537894
431894143994712043942268394043823543450207513886190799409707531632679517
052869104335940723488960240770470438470434329535343866330429132657179201
894810776495469936998716229270764904917198741365340242782600909003168195
629553831589770365472687705483796661474238920271726070390505179067208859
490817765494636249793643314197295308500154814706778732034270622318621910
522030142040283435992446877395852252468365235219657327211742475429216859
612898009146799397834207588995393930733511691021384920256724554594857336
855550714963221355049079118765001875374835520434138927516201876958496564
958805765202364476313555615826884516631224599151532590504446541236893625
713832620042439077419006777861484860386048975978762433100742439296700782
881889486380714070148887484098410694218233687263042755465493793927981497
199521026920386200848153568287674310343346371498689283968784694184354766
679111870702565268681491357079215569781219694309328629243757829281537544
222305623084962270299300645420182502879046175714261919397771509700298570
157891004711917373029290386303109701959096841328964650889891682871446978
568692922345060182670103628056600403977432916893829069098732545636174794
446362475483205590674696119315488543667867514676786440758126850754300452
964368265133082563202580908171650074203739290735941387946242005524276316
413356912394816492851593842390985938520048268384592849898513622096090183
58701821,
podczas gdy druga definicja daje 1403. wyraz o 1 większy.