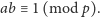Twierdzenie Chevalleya–Warninga i grafy p-regularne
Rozwiązywanie równań diofantycznych jest jednym z ważniejszych
problemów klasycznej teorii liczb. Czytelnicy tego artykułu na pewno
słyszeli o równaniu Pella
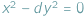 czy równaniu Fermata
czy równaniu Fermata
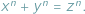
Znane wszystkim Małe Twierdzenie Fermata mówi o rozwiązaniach
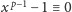 (mod
(mod
 ), a teoria reszt kwadratowych o
), a teoria reszt kwadratowych o
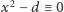 (mod
(mod
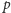 ). Teoria liczb jest nie tylko piękną sztuką, ale także łączy się
z innymi działami nauki, między innymi z kryptografią, topologią czy geometrią
algebraiczną. W tym artykule chciałbym zaprezentować przykład zastosowania
równań diofantycznych w teorii grafów.
). Teoria liczb jest nie tylko piękną sztuką, ale także łączy się
z innymi działami nauki, między innymi z kryptografią, topologią czy geometrią
algebraiczną. W tym artykule chciałbym zaprezentować przykład zastosowania
równań diofantycznych w teorii grafów.
Musimy zacząć od ustalenia kilku ważnych oznaczeń. Jak zwykle
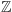 to
zbiór liczb całkowitych. Przez
to
zbiór liczb całkowitych. Przez
 oznaczać będziemy zbiór wszystkich
reszt z dzielenia przez
oznaczać będziemy zbiór wszystkich
reszt z dzielenia przez
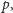 a przez
a przez
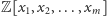 zbiór
wielomianów o zmiennych
zbiór
wielomianów o zmiennych
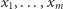 i o współczynnikach
całkowitych.
i o współczynnikach
całkowitych.
Mówimy, że
 -tka liczb całkowitych
-tka liczb całkowitych
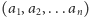 jest
rozwiązaniem modulo
jest
rozwiązaniem modulo
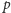 wielomianu
wielomianu
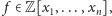 jeżeli
jeżeli
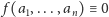 (mod
(mod
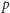 ). Na przykład, para
). Na przykład, para
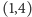 jest
rozwiązaniem modulo
jest
rozwiązaniem modulo
 wielomianu
wielomianu
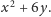
Rozwiązanie
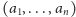 modulo
modulo
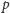 nazywamy istotnym,
jeśli jego współrzędne są liczbami z przedziału od 0 do
nazywamy istotnym,
jeśli jego współrzędne są liczbami z przedziału od 0 do
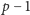 (czyli
(czyli
 dla
dla
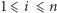 ). W powyższym przykładzie
rozwiązanie
). W powyższym przykładzie
rozwiązanie
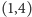 jest istotne, zaś
jest istotne, zaś
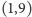 już nie. Z własności
kongruencji wiemy, że jeżeli
już nie. Z własności
kongruencji wiemy, że jeżeli
 jest rozwiązaniem, to
jest rozwiązaniem, to
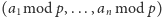 jest rozwiązaniem istotnym. Ponadto, żeby
znaleźć wszystkie rozwiązania modulo
jest rozwiązaniem istotnym. Ponadto, żeby
znaleźć wszystkie rozwiązania modulo
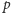 danego równania, wystarczy
znać rozwiązania istotne.
danego równania, wystarczy
znać rozwiązania istotne.
Stopniem jednomianu nazywamy sumę wykładników jego czynników, czyli,
na przykład,
 ma stopień 4. Stopniem wielomianu
ma stopień 4. Stopniem wielomianu
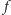 (oznaczamy go
(oznaczamy go
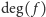 ) nazywamy najwyższy spośród stopni jego
jednomianów; wobec tego dla
) nazywamy najwyższy spośród stopni jego
jednomianów; wobec tego dla
 mamy
mamy
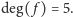
Będziemy wykorzystywać następującą nieoczywistą zależność (której dowód Czytelnik Wnikliwy z pewnością spróbuje znaleźć sam):
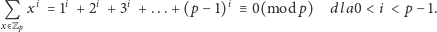 | (1) |
Teraz możemy już zaprezentować tytułowe twierdzenie.
Twierdzenie (Chevalleya–Warninga). Niech
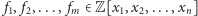 będą niezerowymi
wielomianami wielu zmiennych o sumie stopni mniejszej niż liczba
wszystkich zmiennych, tzn.
będą niezerowymi
wielomianami wielu zmiennych o sumie stopni mniejszej niż liczba
wszystkich zmiennych, tzn.
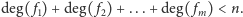 Wtedy liczba ich wspólnych istotnych rozwiązań modulo
Wtedy liczba ich wspólnych istotnych rozwiązań modulo
 jest
podzielna przez
jest
podzielna przez

Zanim zobaczymy dowód twierdzenia, warto przyjrzeć się kilku przykładom i wnioskom. Twierdzenie Chevalleya–Warninga jest ważnym narzędziem w badaniu rozwiązalności równań diofantycznych.
Rozpatrzmy, na przykład, równanie
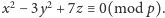 Jego stopień
jest równy dwa, a są trzy zmienne. Zatem z powyższego twierdzenia liczba
rozwiązań istotnych jest podzielna przez
Jego stopień
jest równy dwa, a są trzy zmienne. Zatem z powyższego twierdzenia liczba
rozwiązań istotnych jest podzielna przez
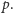 Ten wielomian ma trywialne
rozwiązanie
Ten wielomian ma trywialne
rozwiązanie
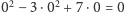 i
i
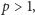 więc musi istnieć także
pewne rozwiązanie nietrywialne, tzn. takie, które ma przynajmniej jedną
współrzędną niezerową. Na przykład, dla
więc musi istnieć także
pewne rozwiązanie nietrywialne, tzn. takie, które ma przynajmniej jedną
współrzędną niezerową. Na przykład, dla
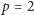 mamy następujące cztery
rozwiązania istotne:
mamy następujące cztery
rozwiązania istotne:
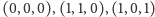 i
i
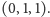
Rozumując podobnie, udowodnimy teraz, że równanie
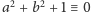 (mod
(mod
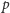 ) ma rozwiązanie. W tym celu przyjrzyjmy się równaniu
) ma rozwiązanie. W tym celu przyjrzyjmy się równaniu
 (mod
(mod
 ).
).
Tak samo jak w poprzednim przykładzie możemy uzasadnić, że istnieje
nietrywialne rozwiązanie
 modulo
modulo
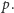 Załóżmy bez straty
ogólności, że
Załóżmy bez straty
ogólności, że
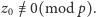 Wtedy
Wtedy
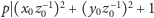 (gdzie
(gdzie
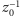 jest odwrotnością
jest odwrotnością
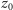 modulo
modulo
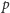 ). A stąd
wnioskujemy, że równanie
). A stąd
wnioskujemy, że równanie
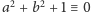 (mod
(mod
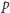 ) ma
rozwiązanie.
) ma
rozwiązanie.
Zwróćmy jeszcze uwagę na pewną delikatną kwestię mogącą wzbudzać
niepokój. Weźmy, na przykład, równanie
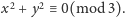 Ma ono
dokładnie jedno istotne rozwiązanie – trywialne. Liczba zmiennych jest
równa stopniowi wielomianu, więc nie możemy stosować twierdzenia
Chevalleya–Warninga. Ale
Ma ono
dokładnie jedno istotne rozwiązanie – trywialne. Liczba zmiennych jest
równa stopniowi wielomianu, więc nie możemy stosować twierdzenia
Chevalleya–Warninga. Ale
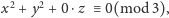 równoważne
naszemu, ma już trzy zmienne i stopień równy 2. Czy zatem otrzymaliśmy
sprzeczność w matematyce? Nie: zmieniła nam się liczba zmiennych i zbiór
rozwiązań jest już trójelementowy:
równoważne
naszemu, ma już trzy zmienne i stopień równy 2. Czy zatem otrzymaliśmy
sprzeczność w matematyce? Nie: zmieniła nam się liczba zmiennych i zbiór
rozwiązań jest już trójelementowy:
Dowód. Przejdźmy do dowodu twierdzenia. Główny pomysł to wyrażenie liczby wspólnych rozwiązań w postaci ładnej funkcji – najlepiej także wielomianu.
Wykażemy najpierw, że wielomian

przystaje do 1 modulo
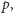 jeżeli
jeżeli
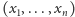 jest wspólnym
rozwiązaniem
jest wspólnym
rozwiązaniem
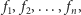 i przystaje do 0 w przeciwnym przypadku.
Dlaczego tak jest? Z Małego Twierdzenia Fermata
i przystaje do 0 w przeciwnym przypadku.
Dlaczego tak jest? Z Małego Twierdzenia Fermata
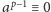 lub
lub
 modulo
modulo
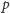 w zależności od tego, czy
w zależności od tego, czy
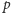 dzieli
dzieli
 czy nie. Zatem
czy nie. Zatem
 -ty czynnik
-ty czynnik
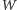 przystaje do
przystaje do
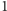 dla
rozwiązania
dla
rozwiązania
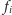 modulo
modulo
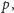 a do
a do
 w przeciwnej
sytuacji.
w przeciwnej
sytuacji.
Wynika stąd, że liczba istotnych rozwiązań przystaje modulo
 do
do

Musimy udowodnić, że ta suma jest podzielna przez
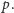
Niech
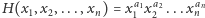 będzie pewnym jednomianem
będzie pewnym jednomianem
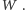 Wykażemy najpierw, że
Wykażemy najpierw, że
 | (2) |
Zauważmy, że

Suma wszystkich wykładników
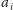 jest mniejsza niż
jest mniejsza niż
 gdyż
gdyż

(ostatnia nierówność wynika z założeń twierdzenia). Dlatego istnieje
przynajmniej jeden wykładnik
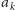 mniejszy niż
mniejszy niż
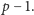 Dla
Dla
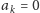 wzór (2) jest prawdziwy, ponieważ
wzór (2) jest prawdziwy, ponieważ
 -ty czynnik
w powyższym iloczynie jest równy
-ty czynnik
w powyższym iloczynie jest równy
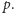 Natomiast dla
Natomiast dla
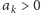 ze
wzoru (1) otrzymujemy
ze
wzoru (1) otrzymujemy

zatem także i cały iloczyn jest podzielny przez
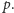
Ponieważ
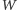 jest sumą swoich jednomianów, to również
jest sumą swoich jednomianów, to również

co należało wykazać.
Użyjemy teraz twierdzenia Chevalleya–Warninga do rozwiązania problemu
z teorii grafów. Stopniem wierzchołka grafu będziemy nazywali liczbę krawędzi
z niego wychodzących. Zakładamy, że graf nie ma pętelek (krawędzi o tym
samym początku i końcu). Mówimy, że graf jest
 -regularny,
jeżeli stopień każdego wierzchołka jest równy
-regularny,
jeżeli stopień każdego wierzchołka jest równy
 Badanie
takich grafów pasjonowało wielu matematyków, szczególnie że – ze
względu na swoją symetrię – naturalnie pojawiają się one w licznych
problemach. Ciągle istnieje wiele nierozwiązanych hipotez dotyczących tej klasy
grafów.
Badanie
takich grafów pasjonowało wielu matematyków, szczególnie że – ze
względu na swoją symetrię – naturalnie pojawiają się one w licznych
problemach. Ciągle istnieje wiele nierozwiązanych hipotez dotyczących tej klasy
grafów.
Twierdzenie (o grafie p-regularnym). Niech
 będzie grafem
będzie grafem
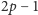 regularnym dla pewnej liczby pierwszej
regularnym dla pewnej liczby pierwszej
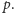 Wtedy w
Wtedy w
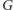 istnieje spójny
istnieje spójny
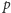 -regularny podgraf.
-regularny podgraf.
Idea dowodu polega na opisaniu świata kombinatorycznego równaniami
diofantycznymi. Niech
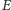 będzie zbiorem krawędzi, a
będzie zbiorem krawędzi, a
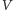 zbiorem
wierzchołków
zbiorem
wierzchołków
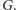 Niech
Niech
 będzie (niekoniecznie spójnym)
podgrafem
będzie (niekoniecznie spójnym)
podgrafem
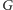 zawierającym wszystkie jego wierzchołki (jak na rysunku).
Krawędzi w
zawierającym wszystkie jego wierzchołki (jak na rysunku).
Krawędzi w
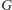 o końcach
o końcach
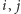 przypiszmy pewną niezerową liczbę
przypiszmy pewną niezerową liczbę
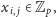 jeżeli ta krawędź leży w
jeżeli ta krawędź leży w
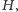 i zero w przeciwnym
przypadku. Stopień
i zero w przeciwnym
przypadku. Stopień
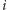 -tego wierzchołka w
-tego wierzchołka w
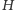 (oznaczany dalej
(oznaczany dalej
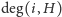 ) przystaje modulo
) przystaje modulo
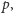 na mocy Małego Twierdzenia
Fermata, do
na mocy Małego Twierdzenia
Fermata, do

I odwrotnie, zauważmy, że każdy wybór liczb
 daje nam
pewien podgraf
daje nam
pewien podgraf
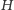 (zakładamy, że zawiera on wszystkie wierzchołki
(zakładamy, że zawiera on wszystkie wierzchołki
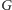 ). Kluczowe w dowodzie jest spostrzeżenie, że wystarczy znaleźć
nietrywialny podgraf
). Kluczowe w dowodzie jest spostrzeżenie, że wystarczy znaleźć
nietrywialny podgraf
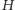 (lub równoważnie liczby
(lub równoważnie liczby
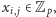 nie
wszystkie zerowe), którego każdy wierzchołek ma stopień podzielny
przez
nie
wszystkie zerowe), którego każdy wierzchołek ma stopień podzielny
przez
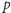 (czyli
(czyli
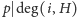 ). Dlaczego? Nietrywialny podgraf
). Dlaczego? Nietrywialny podgraf
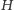 ma nietrywialną spójną składową. Nietrywialna spójna składowa
takiego
ma nietrywialną spójną składową. Nietrywialna spójna składowa
takiego
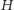 będzie właśnie szukanym
będzie właśnie szukanym
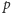 -podgrafem:
-podgrafem:
 i
i
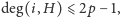 więc
więc
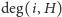 jest
równy 0 lub
jest
równy 0 lub
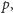 ale w tej nietrywialnej spójnej składowej każdy
wierzchołek będzie miał stopień
ale w tej nietrywialnej spójnej składowej każdy
wierzchołek będzie miał stopień
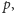 bo wierzchołki stopnia 0 są
izolowane.
bo wierzchołki stopnia 0 są
izolowane.
Udało nam się sprowadzić nasz problem do rozwiązania układu równań diofantycznych

Tych wielomianów jest
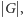 każdy ma stopień
każdy ma stopień
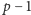 i zależy
od zmiennych
i zależy
od zmiennych
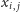 (dla wszystkich
(dla wszystkich
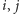 połączonych krawędzią
w
połączonych krawędzią
w
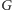 ). Suma stopni tych wielomianów jest równa
). Suma stopni tych wielomianów jest równa
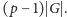 Liczba
zmiennych jest taka sama jak liczba krawędzi w
Liczba
zmiennych jest taka sama jak liczba krawędzi w
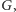 czyli
czyli
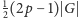 (każdy wierzchołek
(każdy wierzchołek
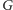 ma stopień
ma stopień
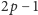 i każda krawędź ma
dwa końce) – to więcej niż
i każda krawędź ma
dwa końce) – to więcej niż
 Ponieważ ten układ równań
diofantycznych ma trywialne rozwiązanie oraz
Ponieważ ten układ równań
diofantycznych ma trywialne rozwiązanie oraz
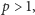 więc z twierdzenia
Chevalleya–Warninga istnieje szukane rozwiązanie nietrywialne.
więc z twierdzenia
Chevalleya–Warninga istnieje szukane rozwiązanie nietrywialne.
Powyższe twierdzenie zostało także udowodnione dla
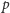 będącego
potęgą liczby pierwszej, ale do tej pory nie wiadomo, czy jest ono prawdziwe dla
dowolnej liczby naturalnej.
będącego
potęgą liczby pierwszej, ale do tej pory nie wiadomo, czy jest ono prawdziwe dla
dowolnej liczby naturalnej.
Łącząc otrzymany przez nas rezultat z argumentami kombinatorycznymi,
można wykazać, że dla
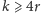 każdy
każdy
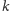 -regularny graf bez
pętelek zawiera podgraf
-regularny graf bez
pętelek zawiera podgraf
 -regularny.
-regularny.
Warto jeszcze zwrócić uwagę, że nie przypadkiem udało nam się opisać
zagadnienie kombinatoryczne za pomocą układu równań diofantycznych.
Można udowodnić metatwierdzenie, że każdy skończony problem
kombinatoryczny (np. dotyczący grafów) można sprowadzić do rozwiązania
pewnego równania diofantycznego modulo
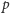 (formalnie, każdy
podzbiór w
(formalnie, każdy
podzbiór w
 jest zbiorem zer pewnego wielomianu). Niestety,
rozwiązanie takiego równania diofantycznego jest prawie zawsze dużo
trudniejsze niż rozwiązanie zagadnienia, od którego wyszliśmy.
jest zbiorem zer pewnego wielomianu). Niestety,
rozwiązanie takiego równania diofantycznego jest prawie zawsze dużo
trudniejsze niż rozwiązanie zagadnienia, od którego wyszliśmy.
 modulo
modulo
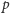 (gdzie
(gdzie
 jest
pierwsza) nazywamy taką liczbę
jest
pierwsza) nazywamy taką liczbę
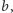 że
że