Cztery zadania, jedno rozwiązanie
Spójrzmy na cztery z pozoru zupełnie niezwiązane zadania...
Zadanie 1.
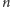 -tą liczbę Fermata definiujemy
wzorem
-tą liczbę Fermata definiujemy
wzorem
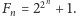 Wykaż, że jeśli
Wykaż, że jeśli
 jest liczbą pierwszą,
która dzieli
jest liczbą pierwszą,
która dzieli
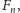 to
to
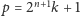 dla pewnej liczby naturalnej
dla pewnej liczby naturalnej
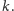
Zadanie 2. Udowodnij, że jeśli
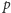 jest liczbą pierwszą różną od 2
i 5, to rozwinięcie dziesiętne
jest liczbą pierwszą różną od 2
i 5, to rozwinięcie dziesiętne
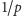 jest ułamkiem okresowym, którego
okres dzieli
jest ułamkiem okresowym, którego
okres dzieli
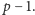
Zadanie 4. Na pewnej tablicy świetlnej można wyświetlać różne konfiguracje za pomocą przełączników. Każdy przełącznik ma ustalony obszar działania. Gdy się go naciśnie, to w jego obszarze zgasną wszystkie zapalone żarówki i zapalą się wszystkie te, które się nie paliły. Wykaż, że liczba konfiguracji, które możemy wyświetlić na tej tablicy, jest potęgą 2.
Może się wydawać, że byłoby bardzo trudno wskazać jakieś wspólne elementy tych problemów. Okazuje się jednak, że rozwiązania wszystkich czterech opierają się na tym samym spostrzeżeniu – fundamentalnej własności pewnych obiektów algebraicznych, o których opowiemy dalej. Spróbujemy odkryć tę własność, rozwiązując ostatnie zadanie.
Tablica świetlna składa się ze zbioru
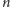 żarówek
żarówek
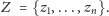 Konfigurację tablicy utożsamimy z podzbiorem
Konfigurację tablicy utożsamimy z podzbiorem
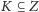 zawierającym dokładnie te żarówki, które są w tej konfiguracji
zapalone. Przełącznikowi natomiast przyporządkujemy podzbiór
zawierającym dokładnie te żarówki, które są w tej konfiguracji
zapalone. Przełącznikowi natomiast przyporządkujemy podzbiór
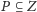 będący obszarem jego działania. W wyniku naciśnięcia
przełącznika
będący obszarem jego działania. W wyniku naciśnięcia
przełącznika
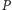 przy wyświetlonej konfiguracji
przy wyświetlonej konfiguracji
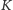 otrzymamy
konfigurację odpowiadającą różnicy symetrycznej
otrzymamy
konfigurację odpowiadającą różnicy symetrycznej

zbiorów
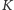 i
i
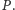 Liczba konfiguracji, które możemy
wyświetlić, jest więc równa liczbie różnych podzbiorów zbioru
Liczba konfiguracji, które możemy
wyświetlić, jest więc równa liczbie różnych podzbiorów zbioru
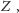 które możemy otrzymać ze zbiorów odpowiadających
przełącznikom, stosując operację „
które możemy otrzymać ze zbiorów odpowiadających
przełącznikom, stosując operację „
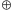 ”.
”.
Przyjrzyjmy się kilku własnościom tej operacji. Wprost z własności różnicy symetrycznej zbiorów wynika, że dla dowolnych konfiguracji:
- i
-
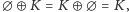
- ii
-
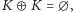
- iii
-
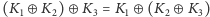 (dzięki temu możemy
pomijać nawiasy).
(dzięki temu możemy
pomijać nawiasy).
Zamiast pojedynczych konfiguracji rozpatrzymy teraz pewne ich zbiory. Niech
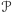 będzie zbiorem przełączników, a
będzie zbiorem przełączników, a
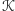 – zbiorem wszystkich
konfiguracji możliwych do otrzymania za ich pomocą z konfiguracji pustej
– zbiorem wszystkich
konfiguracji możliwych do otrzymania za ich pomocą z konfiguracji pustej
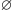 (wszystkie żarówki początkowo zgaszone). Oczywiście, jeśli dwie
konfiguracje
(wszystkie żarówki początkowo zgaszone). Oczywiście, jeśli dwie
konfiguracje
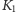 i
i
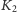 należą do zbioru
należą do zbioru
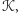 to również
konfiguracja
to również
konfiguracja
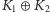 należy do
należy do

Załóżmy teraz, że naszą konfiguracją początkową jest pewna niepusta
konfiguracja
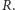 Wtedy zbiór
Wtedy zbiór

opisuje wszystkie konfiguracje możliwe do uzyskania za pomocą przełączników
ze zbioru
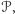 zaczynając od konfiguracji początkowej
zaczynając od konfiguracji początkowej
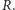 Zastanówmy
się nad związkiem między zbiorami
Zastanówmy
się nad związkiem między zbiorami
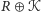 i
i
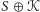 dla
różnych konfiguracji początkowych
dla
różnych konfiguracji początkowych
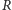 i
i
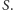 Naturalnym
pytaniem jest, czy za pomocą przełączników ze zbioru
Naturalnym
pytaniem jest, czy za pomocą przełączników ze zbioru
 można
uzyskać tę samą konfigurację, zaczynając od dwóch różnych konfiguracji
początkowych. Załóżmy więc, że zbiory
można
uzyskać tę samą konfigurację, zaczynając od dwóch różnych konfiguracji
początkowych. Załóżmy więc, że zbiory
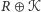 i
i
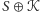 mają
niepustą część wspólną, to znaczy pewna konfiguracja możliwa jest
do uzyskania zarówno z konfiguracji początkowej
mają
niepustą część wspólną, to znaczy pewna konfiguracja możliwa jest
do uzyskania zarówno z konfiguracji początkowej
 jak i z
jak i z
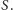 Innymi słowy,
Innymi słowy,
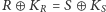 dla pewnych konfiguracji
dla pewnych konfiguracji
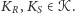 Wtedy na mocy własności dodawania konfiguracji
Wtedy na mocy własności dodawania konfiguracji
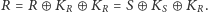
Mamy więc
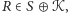 a zatem konfigurację
a zatem konfigurację
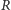 można uzyskać
z konfiguracji
można uzyskać
z konfiguracji
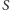 za pomocą przełączników z
za pomocą przełączników z
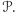 Analogicznie
dowodzimy, że
Analogicznie
dowodzimy, że
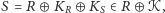 a stąd
a stąd
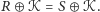
Okazuje się więc, że dla różnych stanów początkowych tablicy zbiory
konfiguracji możliwych do uzyskania za pomocą przełączników ze zbioru
 są takie same lub rozłączne. Zbiór wszystkich możliwych
konfiguracji tablicy dzieli się zatem na sumę rozłącznych zbiorów
są takie same lub rozłączne. Zbiór wszystkich możliwych
konfiguracji tablicy dzieli się zatem na sumę rozłącznych zbiorów
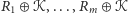 dla pewnych konfiguracji początkowych
dla pewnych konfiguracji początkowych
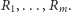 Wykorzystamy jeszcze prostą obserwację, że każdy ze
zbiorów
Wykorzystamy jeszcze prostą obserwację, że każdy ze
zbiorów
 ma tyle samo elementów co
ma tyle samo elementów co
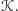 Stąd liczba
wszystkich możliwych konfiguracji tablicy jest wielokrotnością liczby zbiorów
w
Stąd liczba
wszystkich możliwych konfiguracji tablicy jest wielokrotnością liczby zbiorów
w
 Oczywiście, liczba wszystkich konfiguracji tablicy jest
równa
Oczywiście, liczba wszystkich konfiguracji tablicy jest
równa
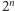 (każda z
(każda z
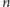 żarówek może być zgaszona lub
zapalona), a więc liczba elementów zbioru
żarówek może być zgaszona lub
zapalona), a więc liczba elementów zbioru
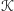 musi być potęgą
dwójki.
musi być potęgą
dwójki.
Decydującą rolę w powyższym rozumowaniu odegrały własności (i)–(iii)
operacji
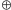 oraz to, że dla dowolnych
oraz to, że dla dowolnych
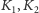 z
z
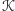 również
również
 jest w
jest w
 Okazuje się, że podobne rozumowanie
można zastosować w wielu innych sytuacjach – w szczególności
w rozwiązaniach pozostałych zadań. Podobnie bowiem dowodzi się twierdzenia
Lagrange’a dotyczącego grup, które stanowi tutaj kluczowy element
rozumowań.
Okazuje się, że podobne rozumowanie
można zastosować w wielu innych sytuacjach – w szczególności
w rozwiązaniach pozostałych zadań. Podobnie bowiem dowodzi się twierdzenia
Lagrange’a dotyczącego grup, które stanowi tutaj kluczowy element
rozumowań.
Rozpatrzmy zbiór
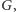 w którym określone jest działanie „
w którym określone jest działanie „
 ”.
Zbiór ten nazwiemy grupą, jeśli działanie „
”.
Zbiór ten nazwiemy grupą, jeśli działanie „
 ” spełnia następujące
warunki:
” spełnia następujące
warunki:
- (1)
- jest łączne, czyli
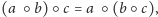
- (2)
- ma element neutralny, oznaczany jako
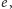 spełniający
spełniający
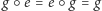 dla dowolnego elementu
dla dowolnego elementu
 z
z
- (3)
- dla każdego elementu
 z
z
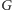 istnieje
element (oznaczany przez
istnieje
element (oznaczany przez
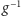 ) odwrotny do niego, czyli taki, że
) odwrotny do niego, czyli taki, że

Podgrupą grupy
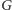 nazywamy podzbiór
nazywamy podzbiór
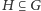 zamknięty na
działanie „
zamknięty na
działanie „
 ” oraz na branie elementu odwrotnego względem tego
działania. To znaczy, że jeśli elementy
” oraz na branie elementu odwrotnego względem tego
działania. To znaczy, że jeśli elementy
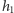 i
i
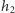 należą do zbioru
należą do zbioru
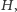 to należą do niego również elementy
to należą do niego również elementy
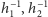 i
i
 Liczbę elementów grupy
Liczbę elementów grupy
 nazywamy jej rzędem
i oznaczamy
nazywamy jej rzędem
i oznaczamy
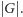
Zauważmy, że określony powyżej zbiór konfiguracji tablicy świetlnej
wraz z operacją „
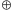 ” jest grupą. Konfiguracja pusta
” jest grupą. Konfiguracja pusta
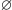 jest
tu elementem neutralnym, a każda konfiguracja
jest
tu elementem neutralnym, a każda konfiguracja
 jest swoją
odwrotnością, gdyż
jest swoją
odwrotnością, gdyż
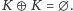 Łatwo również sprawdzić, że
zbiór konfiguracji możliwych do uzyskania za pomocą danego zbioru
przełączników (gdy startuje się z konfiguracji
Łatwo również sprawdzić, że
zbiór konfiguracji możliwych do uzyskania za pomocą danego zbioru
przełączników (gdy startuje się z konfiguracji
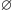 ) jest podgrupą tej
grupy.
) jest podgrupą tej
grupy.
Wspomniane wyżej twierdzenie Lagrange’a brzmi następująco:
Twierdzenie 1 (Lagrange’a).
Jeśli zbiór
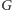 wraz z działaniem „
wraz z działaniem „
 ” jest skończoną grupą,
a
” jest skończoną grupą,
a
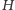 jej podgrupą, to
jej podgrupą, to
 dzieli
dzieli
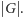
Idea dowodu tego twierdzenia opiera się na pomyśle przedstawionym
w rozwiązaniu zadania: zbiór elementów
 można podzielić
na rozłączne podzbiory postaci
można podzielić
na rozłączne podzbiory postaci
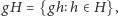 równoliczne
z
równoliczne
z
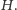
Zastosowanie tego twierdzenia do grupy konfiguracji tablicy świetlnej i jej podgrupy konfiguracji, otrzymywanych za pomocą podanego zbioru przełączników, daje natychmiastowe rozwiązanie zadania 4.
W dalszych rozważaniach będzie użyteczny pewien szczególny przypadek
twierdzenia Lagrange’a. Niech
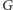 będzie grupą skończoną, a
będzie grupą skończoną, a
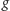 jej
dowolnym elementem. Wtedy istnieje taka liczba naturalna
jej
dowolnym elementem. Wtedy istnieje taka liczba naturalna
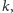 że
element
że
element

(co zapisujemy w skrócie
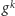 ) jest równy elementowi neutralnemu
grupy
) jest równy elementowi neutralnemu
grupy
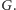 Istotnie, ponieważ grupa
Istotnie, ponieważ grupa
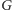 jest skończona, to dla
pewnych liczb naturalnych
jest skończona, to dla
pewnych liczb naturalnych
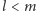 musi zachodzić
musi zachodzić
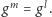 Ale
wtedy
Ale
wtedy
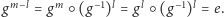
Najmniejszą liczbę
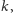 taką że
taką że
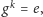 nazywamy rzędem
elementu
nazywamy rzędem
elementu
 i oznaczamy
i oznaczamy
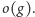 Jest jasne, że elementy
Jest jasne, że elementy
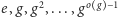 są parami różne oraz
są parami różne oraz
 jest
podgrupą grupy
jest
podgrupą grupy
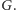 Nazywa się ją podgrupą generowaną przez
Nazywa się ją podgrupą generowaną przez
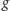 i oznacza
i oznacza
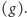 Zatem
Zatem
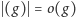 i na mocy twierdzenia
Lagrange’a
i na mocy twierdzenia
Lagrange’a
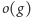 jest dzielnikiem
jest dzielnikiem
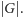 Zauważmy jeszcze,
że jeśli dla pewnej liczby całkowitej
Zauważmy jeszcze,
że jeśli dla pewnej liczby całkowitej
 zachodzi równość
zachodzi równość
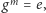 to
to
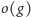 dzieli
dzieli
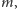 oraz że
oraz że
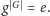
Przyjrzymy się teraz przykładowi – grupie, którą wykorzystamy w rozwiązaniach zadań 1 i 2.
Niech
 będzie liczbą pierwszą. Rozpatrzmy zbiór
będzie liczbą pierwszą. Rozpatrzmy zbiór
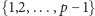 z działaniem „
z działaniem „
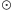 ” określonym dla dowolnych
” określonym dla dowolnych
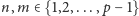 za pomocą wzoru
za pomocą wzoru

Nietrudno sprawdzić, że jest to grupa. Łączność działania „
 ” wynika
z łączności mnożenia, a elementem neutralnym jest 1. Istnienie elementu
odwrotnego do danego elementu
” wynika
z łączności mnożenia, a elementem neutralnym jest 1. Istnienie elementu
odwrotnego do danego elementu
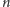 można uzasadnić następująco. Dla
różnych liczb
można uzasadnić następująco. Dla
różnych liczb
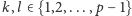 reszty z dzielenia
reszty z dzielenia
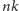 i
i
 przez
przez
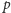 są różne i niezerowe. W przeciwnym razie
mielibyśmy, że
są różne i niezerowe. W przeciwnym razie
mielibyśmy, że
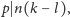 a stąd
a stąd
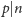 lub
lub
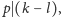 co
jest niemożliwe. Dla pewnego
co
jest niemożliwe. Dla pewnego
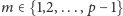 reszta z dzielenia
reszta z dzielenia
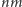 przez
przez
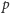 jest więc równa 1, czyli
jest więc równa 1, czyli
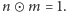
Grupę tę nazywamy grupą multiplikatywną reszt modulo
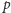 i oznaczamy ją
przez
i oznaczamy ją
przez
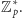 Rząd
Rząd
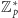 jest, oczywiście, równy
jest, oczywiście, równy
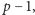 a więc
z tego, co wiemy o własności rzędów elementów, wynika, że w
a więc
z tego, co wiemy o własności rzędów elementów, wynika, że w
 dla dowolnego
dla dowolnego
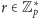 mamy
mamy
 Mamy stąd
natychmiast Małe Twierdzenie Fermata, które mówi, że dla dowolnej liczby
całkowitej
Mamy stąd
natychmiast Małe Twierdzenie Fermata, które mówi, że dla dowolnej liczby
całkowitej
 i dowolnej liczby pierwszej
i dowolnej liczby pierwszej
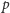 liczba
liczba
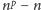 jest
podzielna przez
jest
podzielna przez
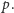
Teraz możemy już rozwiązać pozostałe zadania.
rozwiązanie zadania 1. Załóżmy, że liczba pierwsza
 dzieli
dzieli
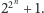 Rozpatrzmy grupę
Rozpatrzmy grupę
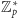 i przyjrzyjmy
się rzędowi elementu
i przyjrzyjmy
się rzędowi elementu
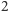 w tej grupie. Z założenia
w tej grupie. Z założenia
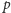 dzieli
liczbę
dzieli
liczbę
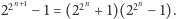 Zatem 2 podniesiona do potęgi
Zatem 2 podniesiona do potęgi
 w
w
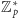 daje
w wyniku 1, a więc
daje
w wyniku 1, a więc
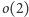 dzieli
dzieli
 Ponieważ jednak 2
do potęgi
Ponieważ jednak 2
do potęgi
 w
w
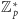 to
to
 więc
więc
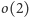 nie dzieli
nie dzieli
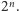 Wiemy zatem, że
Wiemy zatem, że
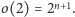 Ponadto
Ponadto
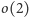 dzieli rząd grupy
dzieli rząd grupy
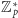 równy
równy
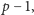 więc dla pewnego naturalnego
więc dla pewnego naturalnego
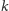 zachodzi równość
zachodzi równość
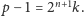 Stąd wynika, że
Stąd wynika, że

rozwiązanie zadania 2. Niech
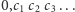 będzie rozwinięciem dziesiętnym liczby
będzie rozwinięciem dziesiętnym liczby
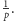 Aby
wyznaczyć to rozwinięcie, wyobraźmy sobie, jak przebiega dzielenie
pisemne 1 przez
Aby
wyznaczyć to rozwinięcie, wyobraźmy sobie, jak przebiega dzielenie
pisemne 1 przez
 Widać, że
Widać, że
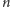 -ta cyfra
-ta cyfra
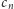 jest
wynikiem dzielenia całkowitego
jest
wynikiem dzielenia całkowitego
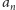 przez
przez
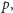 gdzie liczba
gdzie liczba
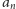 określona jest rekurencyjnie jako reszta
z dzielenia
określona jest rekurencyjnie jako reszta
z dzielenia
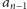 przez
przez
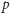 pomnożona przez
pomnożona przez
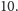 Mamy
więc
Mamy
więc
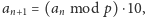 przy czym
przy czym
 Stąd łatwo
otrzymujemy jawny wzór
Stąd łatwo
otrzymujemy jawny wzór
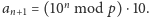
Aby ułamek
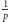 był okresowy, dla pewnych liczb naturalnych
był okresowy, dla pewnych liczb naturalnych
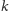 i
i
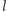 musi zachodzić
musi zachodzić
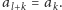 Okresem tego
ułamka nazywa się najmniejszą liczbę
Okresem tego
ułamka nazywa się najmniejszą liczbę
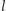 o tej własności. Ponieważ
liczba
o tej własności. Ponieważ
liczba
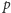 jest różna od
jest różna od
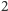 i
i
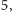 więc
więc
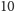 mod
mod
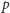 należy do
należy do
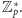 W tej
sytuacji
W tej
sytuacji
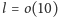 jest najmniejszą liczbą, dla której
jest najmniejszą liczbą, dla której
 jest
równe
jest
równe
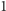 w
w
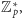 a w konsekwencji
a w konsekwencji
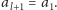 Ułamek
Ułamek
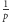 jest więc okresowy, a jego okres równy rzędowi
jest więc okresowy, a jego okres równy rzędowi
 w
w
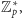 zatem na mocy twierdzenia Lagrange’a dzieli
zatem na mocy twierdzenia Lagrange’a dzieli
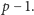
rozwiązanie zadania 3. Zbiór izometrii wielokąta składa się z symetrii osiowych o osiach przechodzących przez jeden punkt i obrotów względem tego punktu. Można wykazać, że wraz z działaniem składania przekształceń tworzy on grupę (jej elementem neutralnym jest obrót o zerowy kąt). Wynika to z następujących geometrycznych własności:
- (1)
- złożenie dwóch obrotów jest obrotem,
- (2)
- złożenie obrotu z symetrią lub symetrii z obrotem jest symetrią,
- (3)
- złożenie symetrii względem przecinających się osi jest obrotem.
Wykażemy najpierw, że jeśli wielokąt ma co najmniej jedną oś symetrii, to
w grupie jego izometrii jest tyle samo symetrii i obrotów. Niech
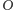 będzie
zbiorem obrotów,
będzie
zbiorem obrotów,
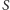 – zbiorem symetrii, a
– zbiorem symetrii, a
 – pewną ustaloną
symetrią danego wielokąta. Wtedy składając
– pewną ustaloną
symetrią danego wielokąta. Wtedy składając
 z dowolnym obrotem,
otrzymamy symetrię. Łatwo też udowodnić, że symetrie
z dowolnym obrotem,
otrzymamy symetrię. Łatwo też udowodnić, że symetrie
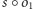 i
i
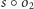 będą różne dla różnych
będą różne dla różnych
 a więc
a więc
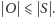 Analogicznie, składając
Analogicznie, składając
 z dowolną symetrią, otrzymamy
obrót, a ponadto
z dowolną symetrią, otrzymamy
obrót, a ponadto
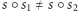 dla różnych
dla różnych
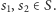 Stąd
Stąd
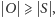 a zatem
a zatem
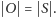
Powodem, dla którego wygodniej rozpatrywać zbiór obrotów
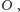 jest zamkniętość tego zbioru na działanie składania przekształceń.
Zbiór obrotów z tym działaniem ma więc strukturę grupy. Jak obroty
zmieniają zbiór wierzchołków wielokąta? Każdy obrót powoduje
pewne cykliczne przesunięcie wierzchołków. Jeśli ponumerujemy kolejne
wierzchołki od
jest zamkniętość tego zbioru na działanie składania przekształceń.
Zbiór obrotów z tym działaniem ma więc strukturę grupy. Jak obroty
zmieniają zbiór wierzchołków wielokąta? Każdy obrót powoduje
pewne cykliczne przesunięcie wierzchołków. Jeśli ponumerujemy kolejne
wierzchołki od
 do
do
 to
to
 -te przesunięcie cykliczne
-te przesunięcie cykliczne
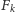 przeprowadza wierzchołek
przeprowadza wierzchołek
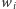 na
na
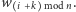 Nietrudno
sprawdzić, że zbiór
Nietrudno
sprawdzić, że zbiór
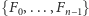 przesunięć cyklicznych
z działaniem składania tworzy grupę. Zbiór obrotów
przesunięć cyklicznych
z działaniem składania tworzy grupę. Zbiór obrotów
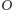 tworzy więc
podgrupę tej grupy, a zatem rząd
tworzy więc
podgrupę tej grupy, a zatem rząd
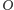 (równy liczbie symetrii danego
(równy liczbie symetrii danego
 -kąta) dzieli
-kąta) dzieli