Mała Delta
Geometryczne liczby
Trzy kółeczka łatwo ułożyć w trójkąt foremny (czyli równoboczny), cztery w czworokąt foremny (czyli kwadrat), pięć w pięciokąt foremny itd. Można więc 3 uważać za liczbę trójkątną, cztery za czworokątną, pięć za pięciokątną itd. Rysunki poniżej pokazują, jak można, rysując kropki, określić inne liczby wielokątne.

Jeśli umówimy się, że 1 jest liczbą
 -kątną dla dowolnego
-kątną dla dowolnego
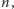 to liczbami trójkątnymi będą
to liczbami trójkątnymi będą
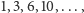 czworokątnymi
czworokątnymi
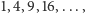 pięciokątnymi
pięciokątnymi
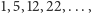 sześciokątnymi
sześciokątnymi
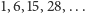 Można znajdować i badać wynikające z obserwacji tych
liczb prawidłowości: np. (n+1)-szą liczbę trójkątną uzyskujemy, dodając do
poprzedniej n+1. Albo: suma
Można znajdować i badać wynikające z obserwacji tych
liczb prawidłowości: np. (n+1)-szą liczbę trójkątną uzyskujemy, dodając do
poprzedniej n+1. Albo: suma
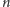 kolejnych liczb nieparzystych to
kolejnych liczb nieparzystych to
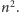 W dawnych wiekach tego rodzaju spostrzeżenia dały początek
pasjonującej do dziś wielu mistyków numerologii. Można też – bardziej
matematycznie – znaleźć ogólny wzór na
W dawnych wiekach tego rodzaju spostrzeżenia dały początek
pasjonującej do dziś wielu mistyków numerologii. Można też – bardziej
matematycznie – znaleźć ogólny wzór na
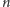 -tą liczbę
-tą liczbę
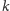 -kątną.
Może on wyglądać, na przykład,
-kątną.
Może on wyglądać, na przykład,

Oczywiście, w podobny sposób można układać z kuleczek wielościany. Gdybyśmy jednak chcieli trzymać się słowa foremny, które wystąpiło w definicji liczb wielokątnych, otrzymalibyśmy tylko pięć takich ciągów, bo istnieje tylko pięć wielościanów foremnych:

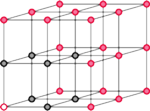
A na dodatek trudno określić, jak miałyby wyglądać kolejne wyrazy takich ciągów – zresztą proszę spróbować.
Dla sześcianu można to sobie jeszcze wyobrazić:
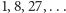 Może
jeszcze dla czworościanu i ośmiościanu daje się coś wymyślić. Ale
np. jak by to było dla dwudziestościanu?
Może
jeszcze dla czworościanu i ośmiościanu daje się coś wymyślić. Ale
np. jak by to było dla dwudziestościanu?
Dlatego więc bardziej popularne są liczby piramidalne.

Jak widać na rysunkach, jest to wynik układania na kulkach reprezentujących
 -tą liczbę
-tą liczbę
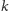 -kątną kulek reprezentujących
-kątną kulek reprezentujących
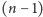 -szą liczbę
-szą liczbę
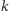 -kątną, aż do pojedynczej kulki.
-kątną, aż do pojedynczej kulki.
Na rysunku z lewej jest piąta liczba piramidalna trójkątna, czyli 35.
Na pozostałych rysunkach można policzyć, ile kulek składa się na piątą liczbę
piramidalną czworokątną i piątą liczbę piramidalną pięciokątną. Ale można
też – korzystając z faktu, że
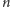 -ta liczba piramidalna
-ta liczba piramidalna
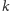 -kątna jest
sumą początkowych
-kątna jest
sumą początkowych
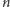 liczb
liczb
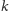 -kątnych – wyprowadzić sobie
wzór na nią. Proszę sprawdzić, że otrzymamy
-kątnych – wyprowadzić sobie
wzór na nią. Proszę sprawdzić, że otrzymamy

Dla liczb piramidalnych czworokątnych będzie to akurat suma kwadratów
początkowych
 liczb. A czy są tu jeszcze jakieś inne ciekawostki?
liczb. A czy są tu jeszcze jakieś inne ciekawostki?
Od sytuacji dwuwymiarowej (wielokąty) przeszliśmy do sytuacji trójwymiarowej (piramidy, czyli wielościany), a co dalej? Gdy braknie nam wyobraźni, zawsze mamy jeszcze możność posługiwania się analogiami. Liczby piramidalne, czyli trójwymiarowe, otrzymaliśmy przez sumowanie liczb wielokątnych, czyli dwuwymiarowych. Możemy więc – przez analogię – przyjąć następującą definicję:
Definicja.
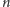 -tą
liczbą
-tą
liczbą
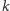 -kątną
-kątną
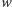 -wymiarową nazywamy liczbę będącą sumą
pierwszych
-wymiarową nazywamy liczbę będącą sumą
pierwszych
 liczb
liczb
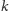 -kątnych
-kątnych
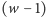 -wymiarowych.
-wymiarowych.
Jakie to liczby? Początek znamy:
 -te liczby
-te liczby
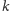 -kątne
dwuwymiarowa i trójwymiarowa to (patrz wyżej)
-kątne
dwuwymiarowa i trójwymiarowa to (patrz wyżej)

Wpadamy więc na pomysł, że może
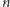 -ta liczba
-ta liczba
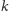 -kątna
czterowymiarowa to
-kątna
czterowymiarowa to

Drogi Czytelniku, sprawdź, korzystając z definicji, że ten pomysł jest rzeczywiście trafny.
A dla prawdziwych Bohaterów Zmagań Rachunkowych mamy do sprawdzenia
dwie postacie wzoru na
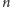 -tą liczbę
-tą liczbę
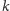 -kątną
-kątną
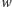 -wymiarową
-wymiarową
