 , czyli jeszcze raz o potęgach dwójki
, czyli jeszcze raz o potęgach dwójki
Aby wykazać, że siódemka jest początkową cyfrą nieskończenie wielu potęg
dwójki, trzeba wyjść poza krąg najprostszych eksperymentów i
zrozumieć, co to znaczy, że zapis dziesiętny liczby
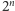 zaczyna się od
siódemki. Otóż, jest tak wtedy, gdy
zaczyna się od
siódemki. Otóż, jest tak wtedy, gdy
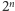 znajduje się między dwiema
liczbami: pierwszą z nich jest siódemka z pewną ilością zer, a drugą –
ósemka z taką samą liczbą zer. Wszystkie liczby między tymi dwiema
zaczynają się od siódemki. I na odwrót, każdą liczbę, która ma za
pierwszą cyfrę siódemkę, można wstawić w jeden z przedziałów
o końcach
znajduje się między dwiema
liczbami: pierwszą z nich jest siódemka z pewną ilością zer, a drugą –
ósemka z taką samą liczbą zer. Wszystkie liczby między tymi dwiema
zaczynają się od siódemki. I na odwrót, każdą liczbę, która ma za
pierwszą cyfrę siódemkę, można wstawić w jeden z przedziałów
o końcach
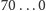 i
i
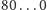 (zer jest w obu liczbach tyle
samo).
(zer jest w obu liczbach tyle
samo).
Teraz, żeby było poręczniej, użyjmy symboli:
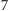 jest pierwszą cyfrą
liczby
jest pierwszą cyfrą
liczby
 wtedy i tylko wtedy, gdy dla pewnego naturalnego
wtedy i tylko wtedy, gdy dla pewnego naturalnego
 mamy
mamy

Aby dostać prostszy, równoważny zapis, logarytmujemy te nierówności
stronami (przy podstawie 10); daje to najpierw
 ,
a ostatecznie
,
a ostatecznie

Możemy tak napisać, gdyż
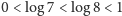 i dlatego
i dlatego
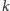 (liczba cyfr
(liczba cyfr
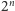 zmniejszona o 1) jest częścią całkowitą liczby
zmniejszona o 1) jest częścią całkowitą liczby
 .
.
Poszukiwanie potęg dwójki z pierwszą cyfrą 7 jest więc tym samym, co
obserwowanie kolejnych wyrazów ciągu
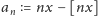 , gdzie
, gdzie
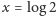 , a
, a
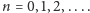
Gdyby np. wziąć
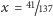 , ciąg
, ciąg
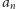 części ułamkowych kolejnych
wielokrotności
części ułamkowych kolejnych
wielokrotności
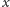 byłby okresowy: wyrazy o numerach różniących się
o 137 byłyby równe. Podobnie byłoby dla każdej liczby wymiernej
byłby okresowy: wyrazy o numerach różniących się
o 137 byłyby równe. Podobnie byłoby dla każdej liczby wymiernej
 .
Jednak
.
Jednak
 nie jest liczbą wymierną: gdyby
nie jest liczbą wymierną: gdyby
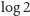 był równy
był równy
 , to wprost z definicji logarytmu mielibyśmy
, to wprost z definicji logarytmu mielibyśmy
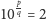 , czyli
, czyli
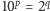 , co jest niemożliwe (lewa strona dzieli się przez
, co jest niemożliwe (lewa strona dzieli się przez
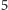 ,
a prawa nie). Kluczową dla nas konsekwencją niewymierności
,
a prawa nie). Kluczową dla nas konsekwencją niewymierności
 jest to, że wszystkie wyrazy ciągu
jest to, że wszystkie wyrazy ciągu
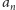 są różne. Gdyby bowiem było
są różne. Gdyby bowiem było
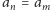 dla jakichś numerów
dla jakichś numerów
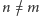 , to przekształcając
równość
, to przekształcając
równość
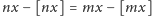 , zapisalibyśmy
, zapisalibyśmy
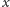 jako
ułamek o liczniku i mianowniku całkowitym,
jako
ułamek o liczniku i mianowniku całkowitym,

a wiemy już, że
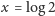 takim ułamkiem nie jest.
takim ułamkiem nie jest.
Te dwa spostrzeżenia pozwalają zrozumieć wszystko do końca. Podzielmy
najpierw odcinek
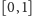 na
na
 równych przedziałów, wybierając
równych przedziałów, wybierając
 tak, żeby długość każdej części była mniejsza niż
tak, żeby długość każdej części była mniejsza niż
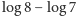 (wystarczy w tym celu wziąć
(wystarczy w tym celu wziąć
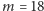 ). Zgodnie
z zasadą szufladkową Dirichleta któreś dwie spośród
). Zgodnie
z zasadą szufladkową Dirichleta któreś dwie spośród
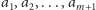 – powiedzmy
– powiedzmy
 i
i
 – należą do tego samego przedziału
długości
– należą do tego samego przedziału
długości
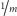 . Jak otrzymać
. Jak otrzymać
 , gdy znamy
, gdy znamy
 ? Nietrudno
to wymyślić:
? Nietrudno
to wymyślić:
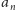 jest częścią ułamkową
jest częścią ułamkową
 , więc jeśli
staniemy na osi liczbowej w punkcie
, więc jeśli
staniemy na osi liczbowej w punkcie
 , zrobimy
, zrobimy
 kroków
długości
kroków
długości
 w prawo i zmierzymy odległość od ostatniej miniętej
liczby całkowitej, to otrzymamy część ułamkową liczby
w prawo i zmierzymy odległość od ostatniej miniętej
liczby całkowitej, to otrzymamy część ułamkową liczby
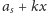 , która
jest równa części ułamkowej liczby
, która
jest równa części ułamkowej liczby
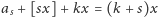 , tzn.
równa
, tzn.
równa
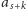 . A to znaczy, że
. A to znaczy, że

jest sumą liczby całkowitej
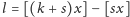 i ułamka
i ułamka
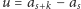 .
Może zachodzi
.
Może zachodzi
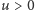 , a może
, a może
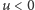 . Tego nie wiemy i na
szczęście jest to nieistotne. Na pewno jednak moduł
. Tego nie wiemy i na
szczęście jest to nieistotne. Na pewno jednak moduł
 nie przekracza
nie przekracza
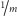 , bo
, bo
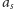 i
i
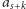 wybraliśmy z tego samego krótkiego
przedziału.
wybraliśmy z tego samego krótkiego
przedziału.
Dla wygody wyobraźmy sobie teraz, że oś liczbowa została nawinięta na
okrąg długości
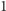 , jak nierozciągliwa nić na szpulkę. W wyniku tej
operacji sklejone zostały końce odcinka
, jak nierozciągliwa nić na szpulkę. W wyniku tej
operacji sklejone zostały końce odcinka
 , a także wszystkie liczby
całkowite. Przesunięciu o
, a także wszystkie liczby
całkowite. Przesunięciu o
 na nitce-osi-liczbowej odpowiada
obrót szpulki-okręgu o kąt równy kątowi środkowemu opartemu na
łuku długości
na nitce-osi-liczbowej odpowiada
obrót szpulki-okręgu o kąt równy kątowi środkowemu opartemu na
łuku długości
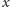 , czyli mówiąc po szkolnemu i nie bawiąc się
w radiany, o kąt
, czyli mówiąc po szkolnemu i nie bawiąc się
w radiany, o kąt
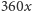 stopni. Przesunięciu o
stopni. Przesunięciu o
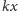 , czyli
, czyli
 -krotnemu przesunięciu o
-krotnemu przesunięciu o
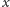 , odpowiada kolejne wykonanie
, odpowiada kolejne wykonanie
 takich obrotów, czyli obrót o
takich obrotów, czyli obrót o
 stopni. Wiemy już,
że jest
stopni. Wiemy już,
że jest
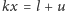 , tzn.
, tzn.
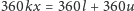 , a obrót
o
, a obrót
o
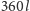 stopni dla całkowitego
stopni dla całkowitego
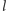 nic przecież nie zmienia.
Na naszej zwiniętej osi liczbowej przejście od
nic przecież nie zmienia.
Na naszej zwiniętej osi liczbowej przejście od
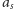 do
do
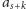 , a także
od jakiegokolwiek
, a także
od jakiegokolwiek
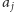 do
do
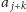 , polega więc na obrocie o kąt
, polega więc na obrocie o kąt
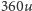 stopni. Może w lewo, a może w prawo; tego nie wiemy.
Dowcip polega jednak na tym, że liczba
stopni. Może w lewo, a może w prawo; tego nie wiemy.
Dowcip polega jednak na tym, że liczba
 ma niewielki moduł
i dlatego
ma niewielki moduł
i dlatego
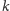 wyjściowych obrotów daje obrót o niewielki kąt.
Zauważmy: dobierając wcześniej odpowiednio dużą liczbę
wyjściowych obrotów daje obrót o niewielki kąt.
Zauważmy: dobierając wcześniej odpowiednio dużą liczbę
 ,
moglibyśmy sprawić, że byłby to obrót o kąt mniejszy od dowolnie
ustalonego.
,
moglibyśmy sprawić, że byłby to obrót o kąt mniejszy od dowolnie
ustalonego.
Na szpulce-zwiniętej-osi jest łuczek-przedział
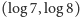 . Dla
dowolnego
. Dla
dowolnego
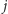 liczby
liczby
 itd. przedzielone są łukami
okręgu długości
itd. przedzielone są łukami
okręgu długości
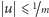 . Ponadto, wszystkie te liczby są różne;
stwierdziliśmy to już dawno. Moglibyśmy je zaznaczyć ołówkiem, stawiając
na okręgu kropki w regularnych odstępach, tak, jak podziałki na zegarku –
tzn. prawie tak, bo wszak zatoczywszy ołówkiem koło, nie trafilibyśmy
ponownie w to samo miejsce. Przedział
. Ponadto, wszystkie te liczby są różne;
stwierdziliśmy to już dawno. Moglibyśmy je zaznaczyć ołówkiem, stawiając
na okręgu kropki w regularnych odstępach, tak, jak podziałki na zegarku –
tzn. prawie tak, bo wszak zatoczywszy ołówkiem koło, nie trafilibyśmy
ponownie w to samo miejsce. Przedział
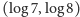 jest dłuższy niż
odstęp między sąsiednimi kropkami. Zatem któraś kropka weń wpadnie.
Jeśli będziemy zaznaczać kropki bez końca, to za każdym pełnym obiegiem
co najmniej jedna z nich znajdzie się na łuku między
jest dłuższy niż
odstęp między sąsiednimi kropkami. Zatem któraś kropka weń wpadnie.
Jeśli będziemy zaznaczać kropki bez końca, to za każdym pełnym obiegiem
co najmniej jedna z nich znajdzie się na łuku między
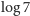 a
a
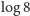 .
Zatem do przedziału
.
Zatem do przedziału
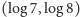 należy nieskończenie wiele
wyrazów ciągu
należy nieskończenie wiele
wyrazów ciągu
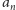 . Nieskończenie wiele potęg dwójki zaczyna się
od siódemki.
. Nieskończenie wiele potęg dwójki zaczyna się
od siódemki.
Identyczne rozumowanie można przeprowadzić dla dowolnego przedziału
 , gdzie
, gdzie
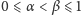 . Wystarczy tak dobrać liczbę
. Wystarczy tak dobrać liczbę
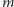 ,
żeby ,,chodzić w kółko odpowiednio drobnymi kroczkami”. Nietrudno stąd
wywnioskować, że każdy skończony ciąg cyfr pojawia się na początku zapisu
dziesiętnego nieskończenie wielu potęg dwójki. Kto zechce, dopracuje
szczegóły.
,
żeby ,,chodzić w kółko odpowiednio drobnymi kroczkami”. Nietrudno stąd
wywnioskować, że każdy skończony ciąg cyfr pojawia się na początku zapisu
dziesiętnego nieskończenie wielu potęg dwójki. Kto zechce, dopracuje
szczegóły.
Czytelnik spostrzegł zapewne, że im przedział
 krótszy, tym więcej
potrzeba w powyższym rozumowaniu wyrazów ciągu
krótszy, tym więcej
potrzeba w powyższym rozumowaniu wyrazów ciągu
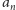 , żeby
któryś z nich do tego przedziału trafił. Po chwili namysłu można wysunąć
przypuszczenie, że liczby
, żeby
któryś z nich do tego przedziału trafił. Po chwili namysłu można wysunąć
przypuszczenie, że liczby
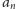 powinny trafiać do przedziału
powinny trafiać do przedziału
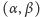 z grubsza proporcjonalnie często do długości tego przedziału.
Tego już nie udowodnimy, ale prawdą jest, że ciąg
z grubsza proporcjonalnie często do długości tego przedziału.
Tego już nie udowodnimy, ale prawdą jest, że ciąg

ma dla
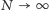 granicę równą
granicę równą
 , czyli owo naturalne
przypuszczenie jest jak najbardziej słuszne. Jest to twierdzenie Bola, Sierpińskiego
i Weyla o równomiernym rozkładzie. Wynika zeń, że częstości początkowych
cyfr liczb
, czyli owo naturalne
przypuszczenie jest jak najbardziej słuszne. Jest to twierdzenie Bola, Sierpińskiego
i Weyla o równomiernym rozkładzie. Wynika zeń, że częstości początkowych
cyfr liczb
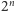 są następujące: 30,1% jedynek, 17,6% dwójek, 12,5% trójek,
9,7% czwórek, 7,9% piątek, 6,7% szóstek, 5,8% siódemek, 5,1% ósemek
i żałosne 4,5% dziewiątek (proszę nie dodawać, bo błędy zaokrągleń wyjdą
na jaw).
są następujące: 30,1% jedynek, 17,6% dwójek, 12,5% trójek,
9,7% czwórek, 7,9% piątek, 6,7% szóstek, 5,8% siódemek, 5,1% ósemek
i żałosne 4,5% dziewiątek (proszę nie dodawać, bo błędy zaokrągleń wyjdą
na jaw).
Takie same są częstości, z jakimi
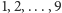 występują na początku
występują na początku
 ,
gdy
,
gdy
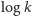 jest niewymierny, a więc gdy
jest niewymierny, a więc gdy
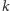 nie jest potęgą dziesiątki.
Na trop tego zjawiska wpadł w 1881 roku Simon Newcomb, astronom
i matematyk, zauważywszy, że tablice logarytmiczne są bardziej wytarte na
początkowych stronach. To samo wykrył pół wieku później Paul Benford,
fizyk zatrudniony w firmie General Electric.
nie jest potęgą dziesiątki.
Na trop tego zjawiska wpadł w 1881 roku Simon Newcomb, astronom
i matematyk, zauważywszy, że tablice logarytmiczne są bardziej wytarte na
początkowych stronach. To samo wykrył pół wieku później Paul Benford,
fizyk zatrudniony w firmie General Electric.
Tak zwane prawo Benforda orzeka, że w różnych pochodzących z życia zestawach danych częstości początkowych cyfr są właśnie takie. W USA urzędy skarbowe i inni tropiciele oszustw finansowych z powodzeniem używają prawa Benforda w walce z tymi, którzy zamiast czytać Deltę, wolą np. seryjnie fałszować czeki i zbyt często wpisują na nich kwoty z dziewiątką na początku (bo w ich banku – począwszy od
– potrzebny jest przy wypłacie dodatkowy podpis kontrolera).
Kto lubi wygodę, płynącą ze stosowania odpowiedniej maszynerii, a roczny wykład analizy matematycznej ma za sobą, niech zajrzy do książki Fomina, Kornfelda i Sinaja o teorii ergodycznej (polski przekład ukazał się w 1987 r.), odszuka podrozdział poświęcony równomiernemu rozkładowi, a następnie sam udowodni twierdzenie Bola, Sierpińskiego i Weyla w paru linijkach (dużo treściwszych niż mój rozgadany tekst). To dzięki temu twierdzeniu wiedziałem, że wystarczy obejrzeć ledwie kilkadziesiąt milionów potęg dwójki, żeby na początku jednej z nich znaleźć właściwą datę. Gdyby Redaktor urodził się np. 17 marca, zadanie byłoby trudniejsze, a ja musiałbym dłużej nie używać laptopa do pracy.