Mam także drugie usprawiedliwienie. 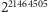ma w zapisie dziesiątkowym blisko sześć i pół miliona cyfr; początkowe z nich to 7, 0, 3, 2, 0, 1 i 0. Ponieważ zaś 7 marca 2010 roku Marek Kordos obchodzi siedemdziesiąte urodziny, więc mogę mu tę potęgę dwójki ofiarować w prezencie, dorzucając do pary 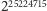– ta z kolei zaczyna się od cyfr 7031940, czyli daty urodzin Redaktora.

Czytelnik, jeśli zechce, potraktuje powyższe dwa zdania jako dowód ostatecznego zdziwaczenia matematyków. Jednak przy okazji przyjdą mu może do głowy pytania: co to za zbieg okoliczności? Dlaczego na początku rozwinięć dziesiętnych potęg dwójki pojawia się data okrągłych urodzin Redaktora? Czy podobny prezent można byłoby zrobić komukolwiek innemu? A może to objaw paranoi? Może autor tekstu, z braku lepszych rozrywek i pomysłów, postanowił zająć się numerologią?

Paranoję i numerologię chętnie zostawiam innym. To, że wśród początkowych fragmentów zapisu dziesiętnego liczb 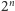 można znaleźć np. 7031940, nie jest wcale szczęśliwym trafem; data urodzin każdego z nas (z numerami PESEL i NIP dorzuconymi na dodatek) znajduje się na początku zapisu dziesiętnego nieskończenie wielu potęg dwójki. To samo można powiedzieć nie tylko o datach. Istnieją np. wykładniki 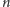 , dla których zapis dziesiętny 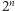 zaczyna się od ciągu utworzonego z wypisanych po kolei wszystkich numerów z książki adresowej mojego telefonu komórkowego. Pisząc te słowa, nie potrafię wprawdzie podać żadnej takiej liczby  , ale mimo to mam uczucie niezachwianej pewności, które nie zawsze towarzyszy mi w życiu. Takie uczucie pewności daje matematykowi dowód – w tym przypadku dowód twierdzenia, które orzeka, że każdy skończony ciąg cyfr pojawia się na początku rozwinięcia dziesiętnego nieskończenie wielu potęg dwójki. (Jedną z pociech, których dostarcza obcowanie z matematyką, jest to, że dzięki dowodom można być pewnym różnych rzeczy nieoczywistych.)

Nawet dla ciągów jednocyfrowych teza owego twierdzenia nie jest oczywista. Gdy zaczniemy wypisywać początkowe cyfry liczb 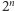dla 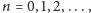to ujrzymy następujący wzór:

Siódemek i dziewiątek jakoś ani śladu, prawda? Co więcej, komuś niecierpliwemu i nieuważnemu może przyjść do głowy myśl, że ciąg początkowych cyfr potęg dwójki jest okresowy i wszystko w nim powtarza się regularnie, co 10 miejsc.

To jednak tylko złudzenie, którego przyczyną jest to, że 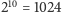jest niezłym przybliżeniem liczby 1000. Mnożenie liczby przez 1000 polega przecież na dopisywaniu trzech zer na końcu jej zapisu dziesiętnego i nie ma najmniejszego wpływu na początkowy fragment tego zapisu. Gdy wielokrotnie mnożymy przez 1024, drobne i początkowo niezbyt istotne dodatki z końcowych fragmentów zapisu dziesiętnego zaczynają kumulować się i wzbierać, rozlewając się stopniowo coraz dalej w lewo. Gdybym wypisał wyżej piąty wiersz początkowych cyfr potęg dwójki, to zamiast szóstki byłaby w nim siódemka.