Trysekcja kąta w "Geometrii" Kartezjusza
Celem tego artykułu jest przybliżenie Czytelnikowi zagadnień i metod matematyki XVII wieku na przykładzie zadania trysekcji kąta i jego rozwiązania przez Kartezjusza. Przeplatają się tu metody geometryczne z algebraicznymi.
Zadanie jest geometryczne i wymagana jest konstrukcja rozwiązania (odcinka). W metodzie zaproponowanej przez Kartezjusza w traktacie Geometria, rozwiązanie tego typu zadań przebiega w dwóch krokach: analiza (resolutio) i synteza (compositio), w następującym ujęciu.
Analiza to ułożenie równania algebraicznego. Składa się z dwóch punktów:
- (a)
- Dla danego zadania geometrycznego zakładamy, że wymagana konstrukcja jest już dokonana i robimy odpowiadający zadaniu rysunek (rys. 1).
- (b)
- Budujemy relacje między odcinkami danymi i odcinkiem szukanym i manipulujemy nimi, aż uzyskamy odpowiednie równanie algebraiczne.
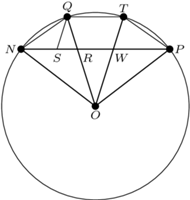
Rys. 1
Synteza to tzw. konstrukcja równania, czyli geometryczna konstrukcja odcinka odpowiadającego rozwiązaniu równania algebraicznego (pierwiastki równania są reprezentowane jako miejsca przecięcia krzywych algebraicznych najniższego możliwego stopnia).
Zobaczmy, jak to wygląda w przypadku zadania trysekcji kąta. Punkt (a) to rysunek 1 na marginesie. Zawiera on już pewien pomysł, narysowanie odcinka 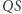 równoległego do odcinka
równoległego do odcinka 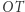 jest jego ważną częścią.
jest jego ważną częścią.
Połóżmy: 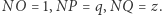 Chcemy znaleźć równanie na
Chcemy znaleźć równanie na  w zależności od
w zależności od 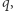 które mamy dane, gdy znamy kąt
które mamy dane, gdy znamy kąt 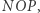 który mamy podzielić.
który mamy podzielić.
Zauważamy, że trójkąty 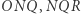 i
i 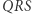 są do siebie podobne (proszę sprawdzić), zatem
są do siebie podobne (proszę sprawdzić), zatem
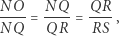 |
(1) |
skąd mamy 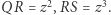 Mamy dalej
Mamy dalej 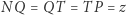 i
i  Ponieważ
Ponieważ 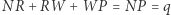 i
i 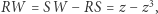 otrzymujemy w końcu równanie algebraiczne, które Kartezjusz zapisuje w postaci
otrzymujemy w końcu równanie algebraiczne, które Kartezjusz zapisuje w postaci
 |
(2) |
Jest oczywiste, że jeśli znamy 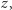 czyli długość odcinka
czyli długość odcinka 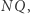 to konstrukcja trysekcji kąta jest zakończona za pomocą dwóch ruchów cyrklem. Zauważmy, że dla
to konstrukcja trysekcji kąta jest zakończona za pomocą dwóch ruchów cyrklem. Zauważmy, że dla 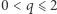 istnienie dodatniego pierwiastka powyższego równania wynika z interpretacji geometrycznej równania.
istnienie dodatniego pierwiastka powyższego równania wynika z interpretacji geometrycznej równania.

Frans Hals (1648)
René Descartes (1596-1650)
Konstrukcja odcinka  należy do części drugiej rozwiązania naszego zadania, czyli do syntezy.
należy do części drugiej rozwiązania naszego zadania, czyli do syntezy.
W Geometrii nasze zadanie rozważane jest jako szczególny przypadek równania 4. stopnia postaci
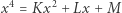 |
(3) |
(do którego Kartezjusz sprowadza ogólne równanie 4. stopnia). Gdy 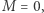 dzieląc powyższe równanie przez
dzieląc powyższe równanie przez 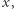 otrzymujemy równanie 3. stopnia postaci (2).
otrzymujemy równanie 3. stopnia postaci (2).
Dokonamy konstrukcji pierwiastków równania (3), przy założeniu, że ma ono cztery pierwiastki rzeczywiste. Ujemne pierwiastki nazywa Kartezjusz fałszywymi, co nie wynika z tego, jakoby "bał się liczb ujemnych", jak to czasem się przedstawia, ale z faktu, że długości odcinków są liczbami dodatnimi. Odrzuca on zatem rozwiązania absurdalne.
Konstrukcję rozwiązań równania (3) sprowadza Kartezjusz do konstrukcji geometrycznej punktów przecięcia paraboli 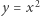 z okręgiem, który należy znaleźć. Zauważmy, że jeśli w równaniu okręgu podstawimy
z okręgiem, który należy znaleźć. Zauważmy, że jeśli w równaniu okręgu podstawimy 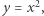 to otrzymamy równanie czwartego stopnia.
to otrzymamy równanie czwartego stopnia.
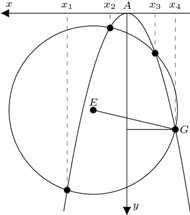
Rys. 2 Ten i następny rysunek to nieco uwspółcześnione wersje oryginalnych rysunków z Geometrii
Równanie okręgu o środku w punkcie 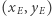 kartezjańskiego prostokątnego układu współrzędnych i promieniu
kartezjańskiego prostokątnego układu współrzędnych i promieniu  ma postać
ma postać
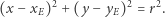 |
(4) |
Sprowadzając to równanie do postaci bez nawiasów, podstawiając w nim 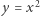 i porównując współczynniki ze współczynnikami w równaniu (3), dostaniemy zależności
i porównując współczynniki ze współczynnikami w równaniu (3), dostaniemy zależności
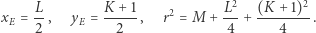 |
(5) |
Można już teraz narysować okrąg, którego odcięte przecięć z parabolą 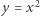 są pierwiastkami równania (3) (Rys. 2). Bardzo możliwe, że Kartezjusz do swojej konstrukcji wykorzystał powyższą metodę współczynników nieoznaczonych (Guicciardini, str. 53).
są pierwiastkami równania (3) (Rys. 2). Bardzo możliwe, że Kartezjusz do swojej konstrukcji wykorzystał powyższą metodę współczynników nieoznaczonych (Guicciardini, str. 53).
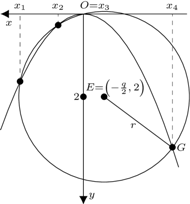
Rys. 3
W przypadku równania (2), w zgodzie z powyższą redukcją równania 4. stopnia do równania 3. stopnia, początek układu współrzędnych i wierzchołek paraboli znajdują się na okręgu, środek okręgu znajduje się w punkcie 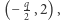 promień okręgu
promień okręgu 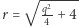 i (dla
i (dla 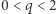 ) mamy trzy rozwiązania równania (2), z których jedno jest "fałszywe", a dwa są dodatnie (Rys. 3). (W Księdze I Geometrii Kartezjusz przedstawia arytmetykę odcinków, czyli konstrukcje odcinków o długości
) mamy trzy rozwiązania równania (2), z których jedno jest "fałszywe", a dwa są dodatnie (Rys. 3). (W Księdze I Geometrii Kartezjusz przedstawia arytmetykę odcinków, czyli konstrukcje odcinków o długości 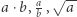 itd., gdy mamy dane odcinki
itd., gdy mamy dane odcinki 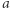 i
i 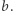 O paraboli zakłada się tu, że jest dana, wykreślona za pomocą przyrządu).
O paraboli zakłada się tu, że jest dana, wykreślona za pomocą przyrządu).
Łatwo sprawdzić, że rozwiązaniem zadania geometrycznego trysekcji kąta 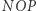 z rysunku 1 jest mniejszy z pierwiastków dodatnich. Zauważmy jednak, że punkty
z rysunku 1 jest mniejszy z pierwiastków dodatnich. Zauważmy jednak, że punkty 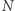 i
i 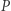 wyznaczają nie jeden, a dwa dopełniające się kąty. Widzimy tutaj, jakie znaczenie ma drugi z dodatnich pierwiastków równania (2). Wyznacza on długość cięciwy stosowanej do trysekcji dopełnienia kąta
wyznaczają nie jeden, a dwa dopełniające się kąty. Widzimy tutaj, jakie znaczenie ma drugi z dodatnich pierwiastków równania (2). Wyznacza on długość cięciwy stosowanej do trysekcji dopełnienia kąta 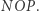 W przypadku skrajnym,
W przypadku skrajnym, 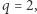 mamy jeden pierwiastek dodatni
mamy jeden pierwiastek dodatni 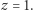 Wtedy styczna do wykresu funkcji
Wtedy styczna do wykresu funkcji 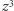 pokrywa się z prostą
pokrywa się z prostą 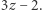 Na koniec warto zauważyć, że ujemny pierwiastek, jakkolwiek geometrycznie absurdalny, jest ściśle powiązany z pozostałymi pierwiastkami, będąc, co do modułu, równy ich sumie. Jest to uniwersalna własność równań 3. stopnia z zerowym współczynnikiem przy wyrazie drugiego rzędu.
Na koniec warto zauważyć, że ujemny pierwiastek, jakkolwiek geometrycznie absurdalny, jest ściśle powiązany z pozostałymi pierwiastkami, będąc, co do modułu, równy ich sumie. Jest to uniwersalna własność równań 3. stopnia z zerowym współczynnikiem przy wyrazie drugiego rzędu.
Zauważmy, że synteza w powyższym przykładzie nie jest prostą odwrotnością analizy, jak to bywa np. w zagadnieniach algebraicznych, gdzie rozumowanie opiera się na ciągu równań prowadzących od hipotezy do tezy, które można przeczytać w odwrotną stronę (ciąg równoważności 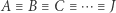 ). W swojej konstrukcji równania Kartezjusz użył krzywych stożkowych, dobrze znanych od starożytności.
). W swojej konstrukcji równania Kartezjusz użył krzywych stożkowych, dobrze znanych od starożytności.

Warto uzmysłowić sobie, że bardzo długo w matematyce dominował paradygmat mówiący o tym, że rozwiązanie zadania to konstrukcja geometryczna, a nie ułożenie równania i wykazanie, że rozwiązania istnieją (konstrukcja rozwiązania nie należy do dzisiejszego paradygmatu matematyki, co niewątpliwie jest jej słabością). Niektórzy autorzy tamtych czasów uważali analizę (resolutio) tylko za część pomocniczą, heurezę, która jest nieelegancka i którą można usunąć w ostatecznej wersji publikacji. Pewność dowodu daje konstrukcja. Także Archimedes chował często źródła swoich pomysłów analitycznych, przedstawiając tylko dowód geometryczny. Wielkim orędownikiem metod geometrycznych, jako dających matematyczną pewność, był Isaac Newton. Wystarczy zajrzeć do Principiów. Kontrowersje co do tego, jak ma wyglądać matematyka i w jakim języku należy ją wyrażać, ciągną sie do współczesności. Dominujący od około 100 lat paradygmat ujęć algebraicznych czy analitycznych w języku abstrakcyjnej symboliki literowej, redukujących geometrię do co najwyżej rysunku pomocniczego, spotyka się stale ze słuszną krytyką znakomitych matematyków i nauczycieli. Niestrudzonym adwokatem metod geometrycznych we współczesnej matematyce był na przykład Władimir Arnold. Tristan Needham z kolei porównuje obecną sytuację do absurdalnego świata muzyki, w którym można tworzyć jedynie partyturę utworu, ale jego wykonywanie jest niemile widziane czy wręcz zakazane. A przecież muzyka to słuchanie, a matematyka to widzenie. Najwyższą formą poznania jest widzenie intuicyjne, jasny i wyraźny obraz.
wikimedia
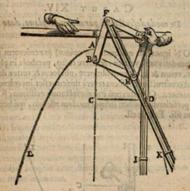
Mechanizm rysujący parabolę
À propos trysekcji klasycznej. Bez wątpienia części Czytelników problem trysekcji kąta skojarzy się z klasycznym problemem jej niewykonalności. Faktycznie, w 1837 roku Pierre Wantzel, uzbrojony w przełomowe idee Évariste'a Galois, dowiódł, że taki podział jest w ogólności (tj. dla dowolnego kąta) niemożliwy do wykonania za pomocą cyrkla i liniału. Jak te fundamentalne fakty mają się do powyższego przepisu? Jak już wiemy, w swojej Geometrii Kartezjusz ułożył równanie
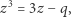 |
gdzie  jest odcinkiem, który należy zbudować, mając dane
jest odcinkiem, który należy zbudować, mając dane 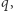 które zależy od kąta, który z kolei mamy podzielić na trzy części.
które zależy od kąta, który z kolei mamy podzielić na trzy części.
Zauważmy, że dla kąta 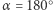 mamy
mamy 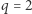 i pierwiastkiem naszego równania jest
i pierwiastkiem naszego równania jest 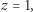 co jest oczywiście równe
co jest oczywiście równe 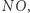 czyli równe promieniowi okręgu, na którym oparty jest kąt
czyli równe promieniowi okręgu, na którym oparty jest kąt 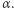 W tym przypadku trysekcja kąta pokrywa się z zadaniem wyznaczenia sześciokąta foremnego.
W tym przypadku trysekcja kąta pokrywa się z zadaniem wyznaczenia sześciokąta foremnego.
Dla kąta 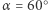 mamy
mamy 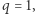 ale w tym przypadku rozwiązanie równania
ale w tym przypadku rozwiązanie równania
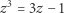 |
(6) |
nie jest konstruowalne za pomocą cyrkla i liniału. Łatwo się o tym przekonać, sprawdzając, że równanie to nie ma pierwiastków wymiernych (wystarczy podstawić 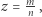 gdzie
gdzie 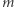 i
i  są liczbami całkowitymi, niemającymi wspólnego dzielnika). Proste rozumowanie prowadzi do wniosku, że
są liczbami całkowitymi, niemającymi wspólnego dzielnika). Proste rozumowanie prowadzi do wniosku, że  powyższej postaci może być równe tylko 1 lub -1. Żadna z tych liczb nie jest rozwiązaniem równania (6). Skorzystaliśmy ze znanego twierdzenia o wielomianach trzeciego stopnia, które jest przystępnie opisane na przykład w książce Couranta i Robbinsa Co to jest matematyka?
powyższej postaci może być równe tylko 1 lub -1. Żadna z tych liczb nie jest rozwiązaniem równania (6). Skorzystaliśmy ze znanego twierdzenia o wielomianach trzeciego stopnia, które jest przystępnie opisane na przykład w książce Couranta i Robbinsa Co to jest matematyka?
Ogólniej, poza pewnymi szczególnymi przypadkami, krokiem przepisu Kartezjusza, który jest niekonstrukcyjny w sensie klasycznym, jest znalezienie punktów przecięcia paraboli i okręgu.
Jeżeli jednak będziemy mniej radykalni i, podobnie jak matematycy XVII wieku, wyjdziemy poza liniał i cyrkiel, poprzez użycie narzędzi takich, jak na przykład ukazany na marginesie mechanizm Franza van Schootena (1615-1660), to okaże się, że procedura Kartezjusza pozwala rozwiązywać równania trzeciego stopnia bez wykonania jakiejkolwiek algebraicznej operacji.