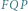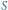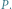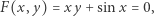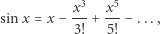Drugie prawo Keplera i owale Newtona. Kontrowersje wokół Lematu XXVIII w "Principiach"

wikipedia
Johannes Kepler (1571-1630)
Drugie prawo Keplera, mówiące o tym, że w równych odstępach czasu promień wodzący planety, poprowadzony od Słońca, zakreśla równe pola (patrz ilustracja na następnej stronie), było w dużym stopniu ignorowane w astronomii przednewtonowskiej. Na przykład w dziele Astronomia Carolina, z którego korzystał Newton, jest ono wyraźnie nieobecne. Wynikało to z jego niewielkiej przydatności do obliczeń położenia planet na ich orbitach.
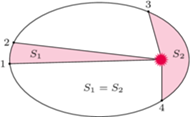
Ilustracja drugiego prawa Keplera.
Załóżmy, że znamy okres 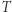 obiegu planety po orbicie eliptycznej. Promień wodzący planety zakreślił w tym czasie znane pole
obiegu planety po orbicie eliptycznej. Promień wodzący planety zakreślił w tym czasie znane pole 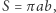 gdzie
gdzie 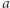 i
i 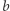 są półosiami elipsy. Rozpoczynając wędrówkę po orbicie w danym punkcie
są półosiami elipsy. Rozpoczynając wędrówkę po orbicie w danym punkcie 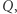 po czasie
po czasie 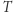 jesteśmy znowu w
jesteśmy znowu w 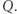 Położenie to jest funkcją czasu obiegu
Położenie to jest funkcją czasu obiegu 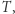 jak i pola
jak i pola 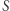 zakreślonego w tym czasie przez promień wodzący planety. Korzystając z drugiego prawa Keplera, możemy teraz znaleźć pole
zakreślonego w tym czasie przez promień wodzący planety. Korzystając z drugiego prawa Keplera, możemy teraz znaleźć pole  sektora zakreślonego przez promień wodzący planety w dowolnym odcinku czasu o długości
sektora zakreślonego przez promień wodzący planety w dowolnym odcinku czasu o długości 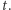 Wydawałoby się, że w tym ogólnym przypadku można także łatwo wyrazić i obliczyć położenie
Wydawałoby się, że w tym ogólnym przypadku można także łatwo wyrazić i obliczyć położenie 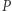 planety na jej orbicie jako funkcję czasu
planety na jej orbicie jako funkcję czasu 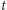 lub zakreślonego w czasie
lub zakreślonego w czasie 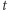 pola
pola 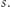 Okazuje się, że tak nie jest.
Okazuje się, że tak nie jest.
Relacja 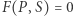 wiążąca położenie
wiążąca położenie 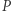 planety na orbicie z polem
planety na orbicie z polem 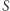 sektora (lub z czasem zakreślenia sektora, gdy skorzystamy z drugiego prawa Keplera) jest przestępna i jej obliczenie prowadzi do szeregów nieskończonych.
sektora (lub z czasem zakreślenia sektora, gdy skorzystamy z drugiego prawa Keplera) jest przestępna i jej obliczenie prowadzi do szeregów nieskończonych.
Praktyczne obliczenia wymagałyby stosowania aproksymacji bardziej kłopotliwych rachunkowo od innych, obmyślonych w tamtych czasach, metod obliczania położenia planet na orbitach. W dodatku sama eliptyczność orbit, ze Słońcem w jednym z ognisk elipsy, stanowiąca treść pierwszego prawa Keplera, była jeszcze kwestionowana. Przykładowo dyrektor Obserwatorium Paryskiego, Giovanni Domenico Cassini, próbował przeforsować krzywe swego własnego pomysłu, znane jako owale Cassiniego.
Z kolei trzecie prawo Keplera, mówiące o tym, że stosunek kwadratu okresu obiegu planety wokół Słońca do sześcianu średniej odległości od Słońca jest stały dla wszystkich planet w Układzie Słonecznym, było dość powszechnie przyjęte, co wynikało z jego zgodności z obserwacjami. Historia recepcji praw Keplera jest dość skomplikowana i ma wiele wątków. Spójny opis można znaleźć np. w książce I. Bernarda Cohena.
W swoich Principiach, czyli Matematycznych Zasadach Filozofii Naturalnej, Newton argumentował, że z drugiego prawa Keplera nie da się ściśle obliczyć położenia planety na orbicie ze względu na przestępność wspomnianej wyżej funkcji. Rozumowanie Newtona dotyczyło zresztą dużo szerszej od elips klasy torów owalnych, nazywanych w dyskusjach owalami Newtona.
Ponieważ Newton nie określił dokładnie, co rozumie przez owal, jego argumentacja została podważona poprzez kontrprzykłady. Jeden z pierwszych podał Gottfried Leibniz. W każdym razie w przypadku elips Newton miał rację. Fascynująca historia kontrowersji wokół poniższego Lematu XXVIII Newtona jest opisana w artykule Bruce'a Pourciau.
Lemat (Lemat XXVIII, Principia, Księga 1). Nulla extat figura Ovalis cujus area rectis pro lubitu abscissa possit per æquationes numero terminorum ac dimensionum finitas generaliter inveniri.
[Nie istnieje figura owalna taka, że pola wszystkich jej segmentów odciętych przez dowolne proste można wyznaczyć w sposób ogólny jako rozwiązania równań wielomianowych].
Możemy to rozumieć tak, że jeśli dowolna prosta 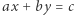 odcina z danego owalu segment o polu
odcina z danego owalu segment o polu 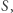 to nie istnieje równanie wielomianowe
to nie istnieje równanie wielomianowe 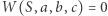 wiążące pole
wiążące pole 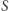 ze współczynnikami
ze współczynnikami 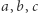 równania tej prostej.
równania tej prostej.
Prawdziwość tego lematu, w przypadku elipsy, implikuje trudności z zastosowaniem drugiego prawa Keplera do obliczania położenia danej planety w dowolnej chwili.
Kontrowersje co do samego lematu wynikają z wątpliwości, co rozumiał Newton przez "figurę owalną". Już Bernoulli, Huygens i Leibniz nie mieli co do tego pełnej jasności, natomiast "dowód" Newtona zdawał się pasować do dowolnej zamkniętej figury. Chcąc się temu zagadnieniu dokładniej przyjrzeć, w tym artykule podamy przykłady "figur owalnych", dla których lemat jest prawdziwy bądź fałszywy. Oryginalny "dowód" Newtona można znaleźć w jego magnum opus.
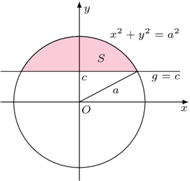
Przykład 1. Rozważmy koło, ograniczone okręgiem 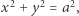 i jego górny segment odcięty prostą
i jego górny segment odcięty prostą 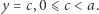 Jeżeli przez
Jeżeli przez 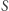 oznaczymy pole tej części, to można obliczyć, że
oznaczymy pole tej części, to można obliczyć, że
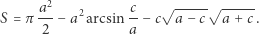 |
W przypadku koła jest to ogólna sytuacja, stąd Lemat XXVIII jest prawdziwy dla tego owalu.
Powyższa zależność jest przestępna, gdyż nie da się jej sprowadzić do zależności wielomianowej. Wykonując obrót koła, a następnie spłaszczając je poprzez transformację 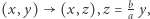 otrzymujemy ogólny wzór wiążący pole segmentu elipsy o półosiach
otrzymujemy ogólny wzór wiążący pole segmentu elipsy o półosiach 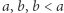 odciętego przez przecinającą ją prostą.
odciętego przez przecinającą ją prostą.
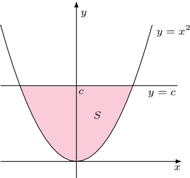
Przykład 2. Rozważmy teraz parabolę 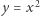 i ograniczony segment nad nią odcięty prostą
i ograniczony segment nad nią odcięty prostą 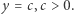 Nie jest to przypadek najogólniejszy, ale sprawdzamy, że pole
Nie jest to przypadek najogólniejszy, ale sprawdzamy, że pole 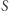 tak określonego obszaru wyraża się poprzez
tak określonego obszaru wyraża się poprzez  zależnością
zależnością
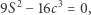 |
a zatem Lemat XXVIII nie jest prawdziwy dla paraboli. Można powiedzieć - zgoda, ale parabola nie jest owalem zamkniętym. Można jednak uzyskać (wypukły) owal zamknięty, zakrywając ją z góry częścią okręgu o promieniu np. 2 i środku na osi 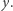
Taki okrąg styka się z naszą parabolą w dwóch punktach i łatwo wykazać, że współczynnik kierunkowy stycznej do uzyskanej figury owalnej zmienia się w sposób ciągły. Mamy zatem gładki (na oko) owal, wypukły, zamknięty, ale przykład 2 pokazuje, że Lemat XXVIII nie jest prawdziwy dla tego owalu, bo odcinanie wycinka paraboli daje zależność algebraiczną.

Przykład 3. Warto jeszcze sprawdzić, jak to jest dla hiperboli, następnej krzywej stożkowej istotnej w astronomii planetarnej. Niech 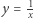 i niech prosta
i niech prosta 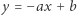 odcina z hiperboli segment ograniczony. Łatwo sprawdzić, że w zależności pola
odcina z hiperboli segment ograniczony. Łatwo sprawdzić, że w zależności pola 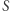 od
od 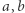 pojawi się funkcja logarytmiczna. Zatem zależność między polem wycinka i parametrami prostej go odcinającej z hiperboli jest przestępna. Zauważmy, że nasz "owal" nie jest zamknięty.
pojawi się funkcja logarytmiczna. Zatem zależność między polem wycinka i parametrami prostej go odcinającej z hiperboli jest przestępna. Zauważmy, że nasz "owal" nie jest zamknięty.
Zapytać można, czym w istocie różni się okrąg od krzywej 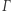 stanowiącej zamknięty owal z przykładu 2. Zarówno okrąg, jak i krzywa
stanowiącej zamknięty owal z przykładu 2. Zarówno okrąg, jak i krzywa 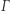 są krzywymi algebraicznymi (można założyć, że tylko takie rozważał Newton - Pourciau, str. 5), zadanymi równaniami wielomianowymi postaci
są krzywymi algebraicznymi (można założyć, że tylko takie rozważał Newton - Pourciau, str. 5), zadanymi równaniami wielomianowymi postaci 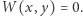 Dokładniej, nasz okrąg jest dany równaniem
Dokładniej, nasz okrąg jest dany równaniem
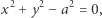 |
(1) |
a każdy punkt krzywej 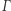 spełnia równanie
spełnia równanie
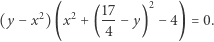 |
(2) |
Może istotnej różnicy należy się doszukiwać w fakcie, że równanie (2) zawiera w sobie nie tylko naszą krzywą 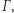 ale też "wąsy", jeden będący półokręgiem, a drugi, ten nieskończony, kawałkiem paraboli. Naprowadza nas to na własność jednoznaczności, odróżniającej wykresy równań (1) i (2). Poruszając się po wykresie równania (1), nie mamy wyboru, pozostajemy na naszym owalu. Inaczej jest w przypadku wykresu równania (2), gdyż możemy zboczyć na któryś z "wąsów" na rozwidleniu w którymś z dwóch punktów styku paraboli z okręgiem. Jest to właściwy ślad, bo taka niejednoznaczność nie może zdarzyć się na krzywych analitycznych, które są w szczególności nieskończenie gładkie. A krzywa
ale też "wąsy", jeden będący półokręgiem, a drugi, ten nieskończony, kawałkiem paraboli. Naprowadza nas to na własność jednoznaczności, odróżniającej wykresy równań (1) i (2). Poruszając się po wykresie równania (1), nie mamy wyboru, pozostajemy na naszym owalu. Inaczej jest w przypadku wykresu równania (2), gdyż możemy zboczyć na któryś z "wąsów" na rozwidleniu w którymś z dwóch punktów styku paraboli z okręgiem. Jest to właściwy ślad, bo taka niejednoznaczność nie może zdarzyć się na krzywych analitycznych, które są w szczególności nieskończenie gładkie. A krzywa 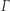 jest gładka tylko na oko!
jest gładka tylko na oko!
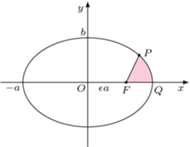
Sektor 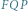 o polu
o polu 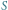 i punkt
i punkt 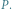
Jeśli umieścimy lokalny kartezjański układ współrzędnych na krzywej 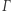 w punkcie styku paraboli z okręgiem, tak aby styczna do niej w tym punkcie stanowiła oś odciętych, a prostopadła do stycznej w tym punkcie oś rzędnych, to wykres krzywej
w punkcie styku paraboli z okręgiem, tak aby styczna do niej w tym punkcie stanowiła oś odciętych, a prostopadła do stycznej w tym punkcie oś rzędnych, to wykres krzywej 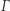 w otoczeniu tego punktu nie jest w naszym lokalnym układzie współrzędnych wykresem funkcji posiadającej wszystkie pochodne. Łatwo sprawdzić, że w punkcie styku nie istnieje już druga pochodna.
w otoczeniu tego punktu nie jest w naszym lokalnym układzie współrzędnych wykresem funkcji posiadającej wszystkie pochodne. Łatwo sprawdzić, że w punkcie styku nie istnieje już druga pochodna.
Analityczność krzywej możemy określić w tym języku następująco. W każdym punkcie krzywej, w lokalnym układzie współrzędnych kartezjańskich opisanym wyżej, krzywa stanowi wykres funkcji mającej lokalnie przedstawienie w postaci szeregu potęgowego 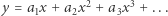

Konstrukcja rozwiązania wykorzystująca równanie Keplera.
Powracamy teraz do drugiego prawa Keplera i zmagań Newtona ze znalezieniem położenia 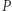 planety w dowolnej chwili
planety w dowolnej chwili 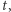 liczonej od przejścia przez perycentrum na orbicie eliptycznej o półosiach
liczonej od przejścia przez perycentrum na orbicie eliptycznej o półosiach 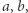 przy założeniu, że czas pełnego obiegu planety po trajektorii (okres obiegu)
przy założeniu, że czas pełnego obiegu planety po trajektorii (okres obiegu) 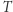 jest znany. Relacja wiążąca
jest znany. Relacja wiążąca 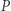 i
i 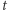 zadana jest słynnym równaniem Keplera
zadana jest słynnym równaniem Keplera
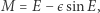 |
gdzie 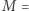 jest anomalią średnią,
jest anomalią średnią, 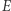 jest anomalią mimośrodową, a
jest anomalią mimośrodową, a  jest mimośrodem orbity. Mamy
jest mimośrodem orbity. Mamy 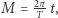 gdzie czas
gdzie czas 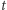 jest związany drugim prawem Keplera z polem
jest związany drugim prawem Keplera z polem 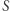 sektora elipsy zakreślonego przez promień wodzący planety,
sektora elipsy zakreślonego przez promień wodzący planety,
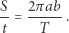 |
Z powyższych wzorów widać, że relacje wiążące pole zakreślonego w czasie 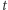 sektora elipsy, a także sam czas
sektora elipsy, a także sam czas 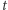 z anomalią mimośrodową
z anomalią mimośrodową 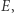 są przestępne. Obliczenie anomalii mimośrodowej można uznać za wskazanie miejsca planety na orbicie (patrz rysunek). Znając
są przestępne. Obliczenie anomalii mimośrodowej można uznać za wskazanie miejsca planety na orbicie (patrz rysunek). Znając 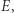 obliczenie współrzędnych punktu
obliczenie współrzędnych punktu 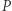 sprowadza się do prostego rachunku. Chcąc obliczyć
sprowadza się do prostego rachunku. Chcąc obliczyć 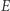 w danej chwili czasu
w danej chwili czasu 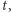 obliczamy
obliczamy 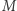 i dalej obliczamy
i dalej obliczamy 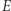 z równania Keplera. Dla tego ostatniego obliczenia Newton zastosował metodę aproksymacji, którą obecnie nazywamy metodą Newtona-Raphsona.
z równania Keplera. Dla tego ostatniego obliczenia Newton zastosował metodę aproksymacji, którą obecnie nazywamy metodą Newtona-Raphsona.
O głębszych aspektach problemów przedstawionych powyżej postaramy się opowiedzieć w następnym artykule.