Wielościany w wielościanach, czyli matematyka eksperymentalna
Czy istnieje coś takiego jak matematyka eksperymentalna? Zobaczmy. Ten tekst zaczniemy od prostego zadania z geometrii, następnie użyjemy komputera, aby rozwiązać je w przybliżeniu, a na koniec z tego przybliżenia zgadniemy dokładny wynik. Będzie też wiele szczegółów do uzupełnienia dla Czytelników. Programy użyte do eksperymentów można znaleźć w [3].
Zadanie z geometrii
Skoro tak dobrze nam poszło, możemy zwiększyć odrobinę stopień trudności:
Za szybko? W takim razie wróćmy do podstaw i spróbujmy powoli uogólnić nasz oryginalny problem w dwóch wymiarach. Kolejnymi kandydatami na uogólnienia są zadania o "Kwadracie w Kwadracie" (mhm...), "Kwadracie w Pięciokącie foremnym" i tak dalej. Moglibyśmy też zapytać o dowolny " 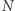 -kąt foremny w
-kąt foremny w 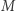 -kącie foremnym". W przypadku najbardziej ogólnego płaskiego problemu:
-kącie foremnym". W przypadku najbardziej ogólnego płaskiego problemu:
Możemy już chyba tylko pomarzyć o eleganckim rozwiązaniu i zdać się na komputer. W ten właśnie sposób dochodzimy do pytania: jak wyrazić nasze zadania w języku zrozumiałym dla komputera?
Programowanie liniowe
Programowanie liniowe pojawiało się niejednokrotnie w Delcie (np.: Kiljan Delta 3/2018, Adamaszek Delta 2/2019, Kowalik Delta 7/2013, Kowalik Delta 2/2020, Wójcik Delta 2/2018). W szkole uczymy się o układach równań liniowych i sposobach ich rozwiązywania. Problem liniowy dopuszcza bardziej ogólnie ograniczenia w postaci równań i nierówności liniowych. Taki układ może mieć zero, jedno lub wiele rozwiązań, a zadaniem programowania liniowego jest znalezienie takiego rozwiązania, które maksymalizuje zadaną funkcję liniową danych zmiennych.

Rys. 1
Dla przykładu rozważmy problem liniowy:
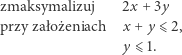 |
Zbiór punktów spełniających założenia tego problemu jest pokazany na rysunku 1 Łatwo sprawdzić, że w tym zbiorze wyrażenie 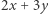 przyjmuje największą wartość 5 w punkcie
przyjmuje największą wartość 5 w punkcie 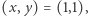 a więc ten punkt jest rozwiązaniem (w tym przypadku jedynym). Problemy liniowe pojawiają się w wielu praktycznych zastosowaniach i, co ważne, można je efektywnie rozwiązywać na komputerze. Procedury do programowania liniowego można znaleźć w większości popularnych pakietów do obliczeń numerycznych, a wyspecjalizowane programy rozwiązują z dużą dokładnością problemy liniowe z milionami zmiennych i ograniczeń.
a więc ten punkt jest rozwiązaniem (w tym przypadku jedynym). Problemy liniowe pojawiają się w wielu praktycznych zastosowaniach i, co ważne, można je efektywnie rozwiązywać na komputerze. Procedury do programowania liniowego można znaleźć w większości popularnych pakietów do obliczeń numerycznych, a wyspecjalizowane programy rozwiązują z dużą dokładnością problemy liniowe z milionami zmiennych i ograniczeń.

Rys. 2
Wyrazimy teraz zadanie o "Kwadracie w Trójkącie" w tym języku. Ustalmy trójkąt 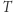 o wierzchołkach
o wierzchołkach 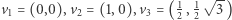 (Rys. 2). Po pierwsze zauważamy, że w języku problemów liniowych możemy opisać postulat "punkt
(Rys. 2). Po pierwsze zauważamy, że w języku problemów liniowych możemy opisać postulat "punkt 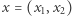 należy do
należy do 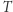 ". Rzeczywiście, są na to nawet dwa sposoby. W sposobie pierwszym wyrażamy fakt, iż punkt
". Rzeczywiście, są na to nawet dwa sposoby. W sposobie pierwszym wyrażamy fakt, iż punkt 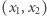 leży po właściwej stronie każdej z prostych zawierających boki trójkąta:
leży po właściwej stronie każdej z prostych zawierających boki trójkąta:
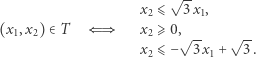 |
Jeżeli nie chcemy pracowicie wyznaczać równań boków trójkąta, możemy użyć innego sposobu. Zapiszemy w nim, że punkt  należy do otoczki wypukłej wierzchołków trójkąta:
należy do otoczki wypukłej wierzchołków trójkąta:
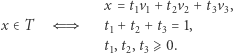 |
Ponieważ współrzędne punktów 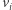 uważamy za stałe, powyższe zależności są liniowe w zmiennych
uważamy za stałe, powyższe zależności są liniowe w zmiennych 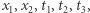 a więc również definiują problem liniowy. Zauważamy też, że obydwa sposoby nadają się do opisania zupełnie dowolnego wielokąta wypukłego
a więc również definiują problem liniowy. Zauważamy też, że obydwa sposoby nadają się do opisania zupełnie dowolnego wielokąta wypukłego 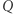 (Dlaczego tylko wypukłego?). Jedyne, czego potrzebujemy, to współrzędne wierzchołków
(Dlaczego tylko wypukłego?). Jedyne, czego potrzebujemy, to współrzędne wierzchołków 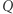 lub równania prostych zawierających boki
lub równania prostych zawierających boki 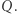
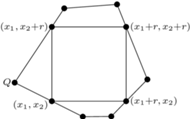
Rys. 3
Potrafimy już zapisać przynależność jednego punktu do ustalonego wielokąta wypukłego 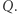 Teraz możemy wreszcie wyrazić zadanie "Kwadrat w
Teraz możemy wreszcie wyrazić zadanie "Kwadrat w 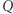 ". Gdyby interesowały nas tylko kwadraty o bokach równoległych do osi współrzędnych, to ułożylibyśmy problem liniowy:
". Gdyby interesowały nas tylko kwadraty o bokach równoległych do osi współrzędnych, to ułożylibyśmy problem liniowy:
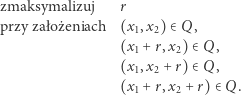 |
(1) |
Faktycznie, jeśli 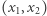 jest lewym dolnym wierzchołkiem szukanego kwadratu, zaś
jest lewym dolnym wierzchołkiem szukanego kwadratu, zaś  jest długością boku (Rys. 3), to cztery podane założenia wyrażają przynależność wszystkich czterech wierzchołków kwadratu do wielokąta
jest długością boku (Rys. 3), to cztery podane założenia wyrażają przynależność wszystkich czterech wierzchołków kwadratu do wielokąta 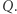 Optymalne rozwiązanie tego problemu liniowego maksymalizuje długość boku
Optymalne rozwiązanie tego problemu liniowego maksymalizuje długość boku 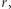 a zatem i pole kwadratu.
a zatem i pole kwadratu.
Jeżeli teraz uwzględnimy w jakiś sposób wszystkie możliwe obroty kwadratu wewnątrz wielokąta, to zadanie będzie rozwiązane! Jesteśmy już bardzo blisko. Dla 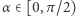 oznaczmy przez
oznaczmy przez 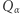 wielokąt
wielokąt 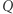 obrócony na płaszczyźnie o kąt
obrócony na płaszczyźnie o kąt 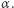 Jeżeli wielokąt
Jeżeli wielokąt 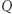 był dany np. poprzez współrzędne wierzchołków, to możemy bardzo łatwo obliczyć wierzchołki wielokąta
był dany np. poprzez współrzędne wierzchołków, to możemy bardzo łatwo obliczyć wierzchołki wielokąta 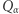 i zapisać problem liniowy:
i zapisać problem liniowy:
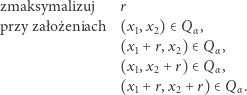 |
(2) |
Oznaczmy rozwiązanie problemu (2) przez 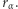 Jest to długość boku największego kwadratu o bokach równoległych do osi, zawartego w
Jest to długość boku największego kwadratu o bokach równoległych do osi, zawartego w 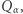 a więc i długość boku największego kwadratu zawartego w
a więc i długość boku największego kwadratu zawartego w 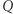 i pochylonego pod kątem
i pochylonego pod kątem 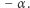 W takim razie
W takim razie 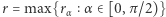 wyznacza długość boku kwadratu, który rozwiązuje zadanie "Kwadrat w
wyznacza długość boku kwadratu, który rozwiązuje zadanie "Kwadrat w 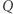 ". (Dlaczego wystarczy ograniczyć się do
". (Dlaczego wystarczy ograniczyć się do 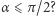 )
)
Rys. 4
Eksperymenty
Oczywiście w praktyce nie możemy rozwiązać problemu (2) dla wszystkich wartości 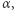 ale możemy wziąć ich wystarczająco wiele, aby naszkicować wykres funkcji
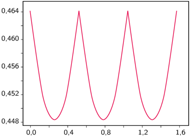
ale możemy wziąć ich wystarczająco wiele, aby naszkicować wykres funkcji 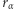 i przybliżyć maksimum z dużą dokładnością. Wróćmy do zadania "Kwadrat w Trójkącie", od którego zaczęliśmy ten tekst. Wykres
i przybliżyć maksimum z dużą dokładnością. Wróćmy do zadania "Kwadrat w Trójkącie", od którego zaczęliśmy ten tekst. Wykres 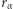 dla tego problemu znajduje się na rysunku 4 Odczytujemy z niego, że maksimum przypada dla obrotu o
dla tego problemu znajduje się na rysunku 4 Odczytujemy z niego, że maksimum przypada dla obrotu o 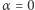 (oraz, oczywiście!,
(oraz, oczywiście!, 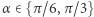 ), tak jak początkowo przypuszczaliśmy. Otrzymujemy też przybliżoną wartość
), tak jak początkowo przypuszczaliśmy. Otrzymujemy też przybliżoną wartość 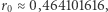 która zgadza się z dokładnym wynikiem do 8. miejsca po przecinku. Jako eksperymentatorzy, jesteśmy usatysfakcjonowani zgodnością teorii z praktyką.
która zgadza się z dokładnym wynikiem do 8. miejsca po przecinku. Jako eksperymentatorzy, jesteśmy usatysfakcjonowani zgodnością teorii z praktyką.
Przejdźmy do zadania "Sześcian w Dwudziestościanie". Wprawdzie rozważania w tekście prowadziliśmy na płaszczyźnie, ale wszystko można powtórzyć w trzech wymiarach z nieznacznymi zmianami. W problemie (2) zamiast czterech wierzchołków kwadratu musimy uwzględnić osiem wierzchołków sześcianu, a zamiast 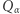 musimy rozważyć wszystkie obroty
musimy rozważyć wszystkie obroty 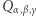 oryginalnej bryły
oryginalnej bryły 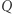 w trzech wymiarach. Po tych poprawkach wciąż mamy serię problemów liniowych obliczających poszczególne wartości
w trzech wymiarach. Po tych poprawkach wciąż mamy serię problemów liniowych obliczających poszczególne wartości 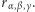
Wierzchołki dwudziestościanu foremnego możemy odszukać w literaturze. Przy oznaczeniu 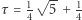 następujące punkty
następujące punkty
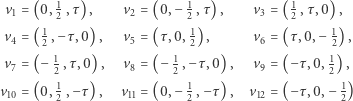 |
stanowią wierzchołki dwudziestościanu foremnego 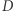 o krawędzi długości 1 i objętości
o krawędzi długości 1 i objętości 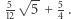 Implementujemy więc trójwymiarową wersję problemu liniowego (2), rozwiązujemy ją w pętli dla kilkuset wartości
Implementujemy więc trójwymiarową wersję problemu liniowego (2), rozwiązujemy ją w pętli dla kilkuset wartości 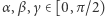 i... czekamy. Po dłuższym czasie otrzymujemy wynik: krawędź sześcianu ma długość w przybliżeniu
i... czekamy. Po dłuższym czasie otrzymujemy wynik: krawędź sześcianu ma długość w przybliżeniu
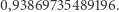 |
(3) |
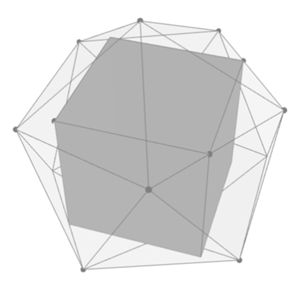
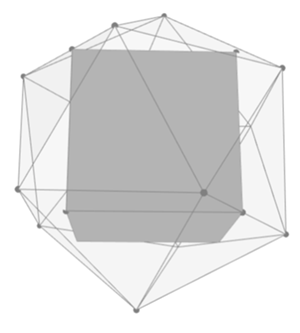
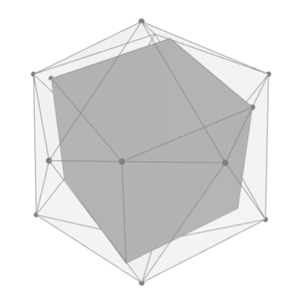
Otrzymujemy także kąty obrotu dające maksymalny sześcian. Możemy to wszystko narysować. Kilka rzutów największego sześcianu wpisanego w dwudziestościan zostało przedstawionych na rysunkach 5-7.
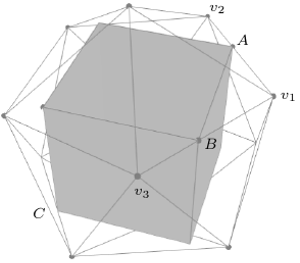
Tak jak poprzednio, domyślamy się, że wynik uzyskany za pomocą komputera nie jest dokładny i że optymalna konfiguracja jakościowo wygląda następująco: dwa wierzchołki 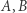 sześcianu leżą symetrycznie na dwóch sąsiednich krawędziach dwudziestościanu, dwa inne wierzchołki
sześcianu leżą symetrycznie na dwóch sąsiednich krawędziach dwudziestościanu, dwa inne wierzchołki 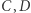 na antypodycznych krawędziach, a pozostałe leżą wewnątrz ścian dwudziestościanu. Czy możemy stąd pokusić się o obliczenie dokładnych wartości? Otóż tak (Rys. 8). Najpierw znajdujemy końce krawędzi dwudziestościanu, na których leżą punkty
na antypodycznych krawędziach, a pozostałe leżą wewnątrz ścian dwudziestościanu. Czy możemy stąd pokusić się o obliczenie dokładnych wartości? Otóż tak (Rys. 8). Najpierw znajdujemy końce krawędzi dwudziestościanu, na których leżą punkty 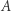 i
i 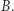 Okazuje się, że bez straty ogólności można w tym celu wybrać
Okazuje się, że bez straty ogólności można w tym celu wybrać 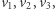 które są w pozycji pokazanej na rysunku. Będziemy zakładać, że
które są w pozycji pokazanej na rysunku. Będziemy zakładać, że
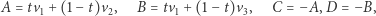 |
dla pewnego 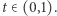 Jak znaleźć
Jak znaleźć 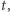 dla którego punkty
dla którego punkty 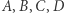 są wierzchołkami sześcianu? Jest wiele sposobów, na przykład spełnione musi być równanie
są wierzchołkami sześcianu? Jest wiele sposobów, na przykład spełnione musi być równanie
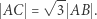 |
Po podstawieniu współrzędnych punktów 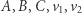 dostajemy równanie kwadratowe w zmiennej
dostajemy równanie kwadratowe w zmiennej 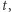 które po nieco uciążliwych przekształceniach (może je wykonać za nas komputer, np. pakiet SAGE), przyjmuje postać:
które po nieco uciążliwych przekształceniach (może je wykonać za nas komputer, np. pakiet SAGE), przyjmuje postać:
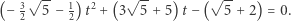 |
Pierwiastkiem tego równania w przedziale 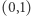 jest
jest 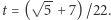 Stąd możemy obliczyć dokładne współrzędne punktów
Stąd możemy obliczyć dokładne współrzędne punktów 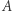 i
i 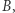 a ostatecznie też długość krawędzi sześcianu
a ostatecznie też długość krawędzi sześcianu
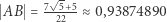 |
(porównaj z (3)) i stosunek objętości sześcianu do dwudziestościanu:
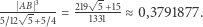 |
Reasumując: przybliżenie uzyskane przy użyciu programowania liniowego okazało się wystarczająco dobre, aby odgadnąć dokładny wynik. Czy to rozumowanie jest pełnym dowodem? Niekoniecznie, ale niedaleko mu do dowodu [?]. Czy to rozumowanie stanowi przekonujące rozwiązanie? Raczej tak. Czy istnieje coś takiego jak matematyka eksperymentalna? Zdecydowanie!