O problemie sadu bez prześwitów
W 1918 roku George Pólya opublikował artykuł Zahlentheoretisches und wahrscheinlichkeits-theoretisches über die Sichtweite im Walde, w którym rozważał następujący problem (w literaturze anglojęzycznej nosi on nazwę Orchard Visibility Problem).

Problem (Orchard Visibility Problem). Sad ma kształt koła o promieniu 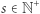 i środku w początku układu współrzędnych. W każdym punkcie kratowym tego sadu, oprócz punktu
i środku w początku układu współrzędnych. W każdym punkcie kratowym tego sadu, oprócz punktu 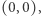 posadzono drzewo. Zakładamy, że każde drzewo ma pień, którego przekrój jest kołem o promieniu
posadzono drzewo. Zakładamy, że każde drzewo ma pień, którego przekrój jest kołem o promieniu 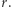 Jakie jest najmniejsze
Jakie jest najmniejsze  dla którego każdy promień wychodzący z punktu
dla którego każdy promień wychodzący z punktu 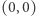 napotyka na swojej drodze jakieś drzewo? Innymi słowy, dla jakich
napotyka na swojej drodze jakieś drzewo? Innymi słowy, dla jakich 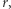 stojąc w punkcie
stojąc w punkcie 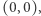 nie zobaczymy w tym sadzie żadnych prześwitów?
nie zobaczymy w tym sadzie żadnych prześwitów?
Zadanie Pólya znalazło się we wspaniałym zbiorze zadań George Pólya i Gábora Szegő Problems and Theorems in Analysis (vol. 2, chap. 5, Problem 239, Springer-Verlag, New York, 1976). Istnieje przekład rosyjski tej książki, niestety nie ma przekładu polskiego.
Eksperymenty
W sformułowaniu zadania z cytowanej książki Pólya i Szegő znajduje się oszacowanie dla poszukiwanego najmniejszego 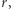 my jednak rozpoczniemy od eksperymentalnej analizy zagadnienia. Eksperymenty przeprowadzono za pomocą programu GeoGebra, korzystając z dwóch suwaków (dla
my jednak rozpoczniemy od eksperymentalnej analizy zagadnienia. Eksperymenty przeprowadzono za pomocą programu GeoGebra, korzystając z dwóch suwaków (dla  oraz dla
oraz dla  ). Zamieszczone poniżej zrzuty ekranów dotyczą przypadków, gdy
). Zamieszczone poniżej zrzuty ekranów dotyczą przypadków, gdy 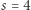 oraz
oraz 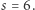

W obu przypadkach minimalny promień 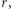 dla którego jakaś półprosta wychodząca z punktu
dla którego jakaś półprosta wychodząca z punktu 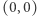 napotka drzewo, jest w przybliżeniu równy
napotka drzewo, jest w przybliżeniu równy 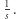 Kolejne spostrzeżenie wynika z symetrii. Otóż drzewa w kole położone są symetrycznie względem obu osi układu, więc wystarczy rozpatrzyć I ćwiartkę koła (sadu) i ograniczyć się do drzew o środkach w punktach
Kolejne spostrzeżenie wynika z symetrii. Otóż drzewa w kole położone są symetrycznie względem obu osi układu, więc wystarczy rozpatrzyć I ćwiartkę koła (sadu) i ograniczyć się do drzew o środkach w punktach 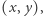 przy czym
przy czym 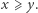
Minimalny promień drzew dla sadu bez prześwitów - łatwiejsza część

Udowodnimy, że jeśli  to sad ma prześwit. Spójrzmy na fragment sadu przedstawiony na marginesie (rozumowanie jest ogólne, ilustrujemy je dla
to sad ma prześwit. Spójrzmy na fragment sadu przedstawiony na marginesie (rozumowanie jest ogólne, ilustrujemy je dla  ). Odległość punktów
). Odległość punktów 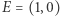 i
i  od półprostej
od półprostej 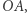 gdzie
gdzie 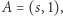 wynosi
wynosi 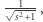 stąd drzewa w punkcie
stąd drzewa w punkcie 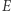 oraz w punkcie
oraz w punkcie 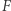 o promieniu
o promieniu 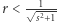 nie dotykają półprostej
nie dotykają półprostej  Zatem jeśli sad nie ma prześwitów, to
Zatem jeśli sad nie ma prześwitów, to 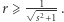 Uzasadnienie, że promień
Uzasadnienie, że promień 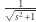 faktycznie jest najmniejszym możliwym, jest już bardziej złożone.
faktycznie jest najmniejszym możliwym, jest już bardziej złożone.
Minimalny promień drzew - trudniejsza część
Zauważmy najpierw, że kluczowe dla rozpatrywanego problemu są drzewa posadzone w punktach 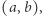 gdzie
gdzie 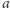 oraz
oraz 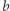 są względnie pierwsze. Tak rzeczywiście jest, gdyż jeśli
są względnie pierwsze. Tak rzeczywiście jest, gdyż jeśli 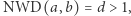 to drzewo w punkcie
to drzewo w punkcie 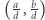 zasłania drzewo w punkcie
zasłania drzewo w punkcie  Przypomnijmy, że prześwity sadu obserwujemy z punktu
Przypomnijmy, że prześwity sadu obserwujemy z punktu  Rozpatrzmy więc wszystkie punkty w sadzie o współrzędnych względnie pierwszych. Dla
Rozpatrzmy więc wszystkie punkty w sadzie o współrzędnych względnie pierwszych. Dla  w pierwszej ćwiartce takich punktów jest łącznie trzynaście. Wszystkie te punkty można znaleźć, stosując algorytm Sterna-Brocota, który polega na prostej operacji sumowania punktów. Opiszemy go właśnie dla
w pierwszej ćwiartce takich punktów jest łącznie trzynaście. Wszystkie te punkty można znaleźć, stosując algorytm Sterna-Brocota, który polega na prostej operacji sumowania punktów. Opiszemy go właśnie dla 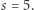
Rozpoczynamy od pary punktów  i
i 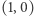 (etap I), a następnie na każdym kolejnym etapie pomiędzy dwa sąsiednie punkty z poprzedniego etapu wstawiamy punkt, którego współrzędne to sumy odpowiednich współrzędnych punktów sąsiednich. Popatrzmy na punkty otrzymane w kolejnych etapach tej procedury:
(etap I), a następnie na każdym kolejnym etapie pomiędzy dwa sąsiednie punkty z poprzedniego etapu wstawiamy punkt, którego współrzędne to sumy odpowiednich współrzędnych punktów sąsiednich. Popatrzmy na punkty otrzymane w kolejnych etapach tej procedury:

Zauważmy, że cztery punkty z etapu V nie należą do rozpatrywanego sadu - zaznaczono je kolorem na rysunku poniżej . 13 kluczowych dla naszego problemu punktów ma kolor czarny, pozostałe punkty są nieistotne. Otrzymane za pomocą algorytmu Sterna-Brocota na każdym etapie punkty mają ważne, łatwe do udowodnienia własności:

- jeśli punkty
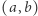 oraz
oraz 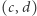 są sąsiednie, to
są sąsiednie, to 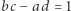 ;
; 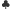
- punkty
 w odniesieniu do ilorazu
w odniesieniu do ilorazu 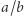 są uporządkowane rosnąco, co oznacza także, że kąt, jaki tworzy półprosta łącząca
są uporządkowane rosnąco, co oznacza także, że kąt, jaki tworzy półprosta łącząca 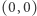 i
i 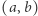 z dodatnią półosią
z dodatnią półosią 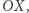 maleje.
maleje.


Rozpatrzmy parę sąsiednich punktów na jakimś etapie procedury Sterna-Brocota, które leżą w kole o promieniu  (nazwijmy te punkty
(nazwijmy te punkty 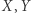 ), oraz takich, że punkt
), oraz takich, że punkt 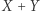 leży poza tym kołem. Na rysunku takimi punktami są na przykład
leży poza tym kołem. Na rysunku takimi punktami są na przykład 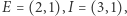 punkt
punkt 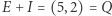 leży na zewnątrz koła. Czwórka punktów
leży na zewnątrz koła. Czwórka punktów  tworzy równoległobok bez punktów kratowych wewnątrz. Kluczowe dla dalszych rozumowań jest poniższe twierdzenie.
tworzy równoległobok bez punktów kratowych wewnątrz. Kluczowe dla dalszych rozumowań jest poniższe twierdzenie.
Twierdzenie. Niech 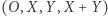 będzie czwórką punktów opisaną powyżej, przy czym
będzie czwórką punktów opisaną powyżej, przy czym 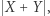 czyli odległość punktu
czyli odległość punktu  od punktu
od punktu 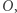 jest najmniejszą możliwą. Wówczas sad z drzewami o promieniu
jest najmniejszą możliwą. Wówczas sad z drzewami o promieniu  nie ma prześwitów wtedy i tylko wtedy, gdy
nie ma prześwitów wtedy i tylko wtedy, gdy 
Dowód. Spójrzmy na rysunek na marginesie. Jeżeli pomiędzy drzewami znajdującymi się w punktach 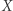 i
i 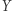 jest prześwit, to pomiędzy nimi będzie widoczne drzewo w punkcie
jest prześwit, to pomiędzy nimi będzie widoczne drzewo w punkcie 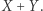 Ponieważ
Ponieważ 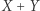 znajduje się poza sadem, oznacza to, że nie możemy dopuścić do tego prześwitu. Zauważmy najpierw, że odległość punktów
znajduje się poza sadem, oznacza to, że nie możemy dopuścić do tego prześwitu. Zauważmy najpierw, że odległość punktów 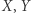 od prostej łączącej
od prostej łączącej 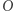 z
z 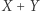 wynosi
wynosi  Wynika to z tego, że pole równoległoboku
Wynika to z tego, że pole równoległoboku  jest równe 1 (własność
jest równe 1 (własność 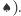 Ponadto z własności
Ponadto z własności 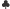 wynika, że w wycinku
wynika, że w wycinku  rozpatrywanego koła nie ma punktów kratowych. Zatem jeśli
rozpatrywanego koła nie ma punktów kratowych. Zatem jeśli 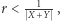 to półprosta łącząca
to półprosta łącząca 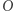 z
z 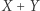 nie napotyka w sadzie żadnego drzewa.
nie napotyka w sadzie żadnego drzewa.
Załóżmy teraz, że 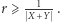 Pokażemy, że w sadzie w pasie między zaznaczonymi kolorem prostymi nie ma żadnych punktów kratowych o współrzędnych względnie pierwszych. Niech
Pokażemy, że w sadzie w pasie między zaznaczonymi kolorem prostymi nie ma żadnych punktów kratowych o współrzędnych względnie pierwszych. Niech 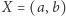 oraz
oraz 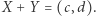 Obie proste w kolorze są równoległe do prostej łączącej
Obie proste w kolorze są równoległe do prostej łączącej 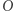 z
z  zatem równania kolorowych prostych są postaci:
zatem równania kolorowych prostych są postaci:
 |
Stąd jeśli punkt kratowy 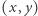 leży w rozpatrywanym zbiorze, to otrzymujemy:
leży w rozpatrywanym zbiorze, to otrzymujemy:
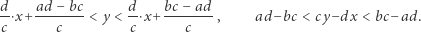 |
Zatem  czyli punkt
czyli punkt 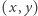 o współrzędnych względnie pierwszych leży na prostej łączącej
o współrzędnych względnie pierwszych leży na prostej łączącej  z
z  ale jedynym takim punktem z "listy" Brocota-Sterna jest punkt
ale jedynym takim punktem z "listy" Brocota-Sterna jest punkt 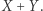
Z nierówności 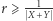 wynika, że prosta łącząca
wynika, że prosta łącząca 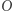 z
z 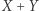 nie może ominąć drzewa w punkcie
nie może ominąć drzewa w punkcie 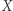 ani
ani 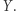 Jeśli weźmiemy inną czwórkę punktów
Jeśli weźmiemy inną czwórkę punktów  przy czym punkty
przy czym punkty  leżą w sadzie i każdy z nich ma współrzędne względnie pierwsze oraz punkt
leżą w sadzie i każdy z nich ma współrzędne względnie pierwsze oraz punkt 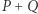 leży na zewnątrz sadu, to
leży na zewnątrz sadu, to  oraz
oraz 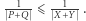 Jeśli weźmiemy promień drzewa równy
Jeśli weźmiemy promień drzewa równy 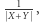 to prosta łącząca
to prosta łącząca 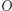 z
z 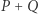 nie ominie punktu
nie ominie punktu 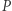 ani
ani 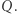
Możemy teraz postawić kropkę nad i - znaleźć minimalny promień drzew dla sadu bez prześwitów. Z twierdzenia wynika, że dla dowolnej liczby całkowitej  ten minimalny promień oblicza się ze wzoru
ten minimalny promień oblicza się ze wzoru
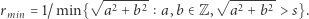 |
Oczywiście 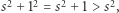 więc
więc