Rachunki

O nierówności między średnią arytmetyczną sinusa i tangensa kąta ostrego a jego miarą

Celem tego artykułu jest wykazanie prawdziwości nierówności 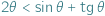$|2` < sin` + tg`$ dla dowolnego kąta ostrego 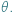$`:$ Podaną nierówność można łatwo udowodnić, używając rachunku różniczkowego. Można jednak zadać pytanie: czy da się tego uniknąć, czy można ją wykazać krócej, używając przy tym jedynie elementarnej geometrii. Okazuje się, że tak.

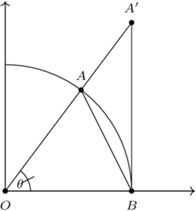
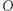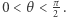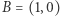Rozważmy okrąg jednostkowy o środku w początku $O$ układu współrzędnych i ustalmy dowolny kąt $π 0 < θ < 2 .$ Niech $|B = (1,0)$ i obierzmy taki punkt 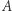$|A$ leżący na okręgu jednostkowym w pierwszej ćwiartce, że 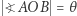$| ?AOB$ ; na półprostej 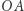$OA$ tak obierzmy zaś punkt 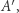$A |$ aby trójkąt 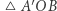$| A$ był prostokątny, o kącie prostym 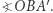$|?OBA$ Zostało to przedstawione na rysunku 1.

Łatwo można dostrzec, że

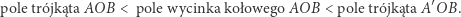pole trójkąta AOB

Obliczmy teraz kolejno pola wymienionych figur. Po pierwsze zachodzi

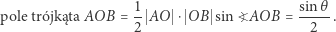pole trójkąta AOB

Znany jest także wzór na pole wycinka kołowego o danej rozwartości, który mówi, iż

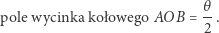pole wycinka kołowego AOB

Ponieważ zachodzi równość 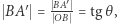$BA ,$ to

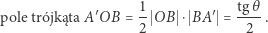pole trójkąta A

Otrzymaliśmy w ten sposób geometryczny dowód związku między wartościami funkcji trygonometrycznych kąta ostrego a jego miarą.

Twierdzenie. Dla dowolnej liczby 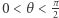$0 < θ < π2$ zachodzi nierówność

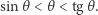sin θ< θ < tg θ.

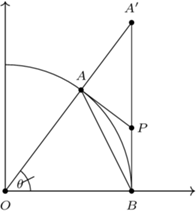
Wykorzystane w dowodzie powyższego twierdzenia geometryczne konstrukcje przydadzą się nam do wykazania podanej we wstępie nierówności. Poprowadźmy styczną w punkcie 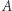$A$ do okręgu, przecinającą odcinek 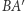$|BA$ w punkcie 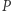$P |$ (Rys. 2).

Z twierdzenia o odcinkach stycznych do okręgu wiemy, iż 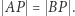$| AP$ Odcinek 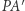$|PA$ jest przeciwprostokątną trójkąta 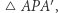$APA$ odcinek 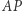$AP$ jest zaś jego przyprostokątną, zatem 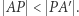$AP$ Z powyższych własności wynika, że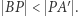 $| BP < PA$

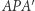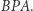Rozważmy teraz trójkąty $APA$ i $BPA. |$ Mają one tę samą wysokość opuszczoną na prostą 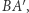$|BA$ skoro zaś podstawa tego pierwszego jest dłuższa od podstawy drugiego, to

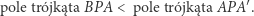pole trójkąta BPA

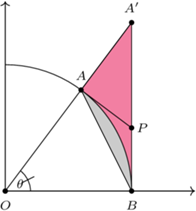
Wiemy już, polami czego są wielkości 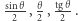$sinθ ,θ, tgθ. 2 2 2$ Spójrzmy więc na rysunek 3, na którym na szaro zaznaczono figurę o polu 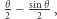$|θ sinθ 2− 2 ,$ kolorem zaś figurę o polu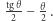 $tgθ -2-− θ2 .$

Łatwo zauważyć, że

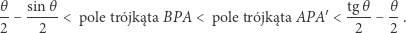θ-− sin-θ-< pole trójkąta BPA 2 2

Udowodniliśmy tym samym następującą zależność.

Twierdzenie. Dla dowolnej liczby 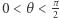$0 < θ < π2$ zachodzi nierówność

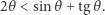2θ< sinθ + tg θ.