Ślad ruchomego odcinka
Choć ruch jest wszechobecny w naszym otoczeniu, to opis dynamicznych zmian będących jego wynikiem sprawia nam kłopot. Oto kilka prostych obserwacji...
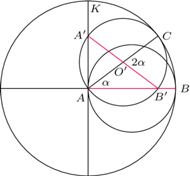
Rys. 1.
Fakt. Gdy okrąg toczy się bez poślizgu po wewnętrznej stronie nieruchomego okręgu o dwa razy większej średnicy, to dowolnie wybrany punkt mniejszego okręgu przesuwa się po średnicy dużego okręgu tam i z powrotem.
Wykażemy, że tak jest. Na małym okręgu ustalmy punkty 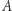 i
i 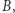 tak jak na rysunku 1. Gdy mały okrąg toczy się po łuku
tak jak na rysunku 1. Gdy mały okrąg toczy się po łuku 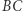 i kąt
i kąt  to przecina odcinek
to przecina odcinek 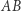 w takim punkcie
w takim punkcie 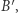 że kąt
że kąt 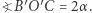 Wówczas łuki
Wówczas łuki  oraz
oraz 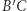 są tej samej długości. Oznacza to, że podczas toczenia małego okręgu punkt
są tej samej długości. Oznacza to, że podczas toczenia małego okręgu punkt 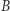 przesuwa się do punktu
przesuwa się do punktu  wzdłuż prostej
wzdłuż prostej 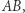 co chcieliśmy uzasadnić.
co chcieliśmy uzasadnić.
Zauważmy, że w tym samym czasie punkt 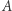 przesuwa się do punktu
przesuwa się do punktu 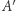 wzdłuż prostej
wzdłuż prostej 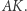 Punkt
Punkt 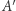 z punktem
z punktem 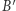 są końcami średnicy małego okręgu (bo łuki
są końcami średnicy małego okręgu (bo łuki 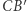 i
i  są równej długości), więc kąt
są równej długości), więc kąt  jest prosty. Mamy więc dodatkową informację: podczas opisanego toczenia końce odcinka
jest prosty. Mamy więc dodatkową informację: podczas opisanego toczenia końce odcinka  ślizgają się po wzajemnie prostopadłych średnicach większego okręgu.
ślizgają się po wzajemnie prostopadłych średnicach większego okręgu.
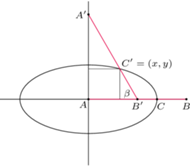
Rys. 2.
Okazuje się, że:
Fakt. Każdy punkt pośredni odcinka  którego końce ślizgają się po wzajemnie prostopadłych prostych, zakreśla elipsę (Rys. 2).
którego końce ślizgają się po wzajemnie prostopadłych prostych, zakreśla elipsę (Rys. 2).
Wiedział to już Proklos (412-485). Uzasadnienie jest łatwe. Ponieważ

więc z zależności

mamy

a to jest równanie elipsy. Analogiczna sytuacja ma miejsce, gdy punkt zakreślający krzywą leży na przedłużeniu odcinka 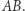 Mamy zatem kolejną obserwację:
Mamy zatem kolejną obserwację:
Fakt. Jeśli punkty 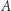 i
i 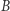 prostej
prostej 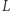 ślizgają się po wzajemnie prostopadłych prostych, to każdy inny punkt prostej
ślizgają się po wzajemnie prostopadłych prostych, to każdy inny punkt prostej 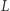 zakreśla elipsę.
zakreśla elipsę.

Rys. 3.
Rezultat ten jest podstawą konstrukcji "cyrkla" do wykreślania elipsy o danym środku, danych kierunkach głównych i danych długościach osi (Rys. 3).
A jak wygląda sytuacja, gdy punkty 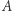 i
i 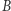 ślizgają się po ramionach kąta
ślizgają się po ramionach kąta 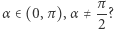 Problem ten rozstrzygnął w 1646 roku Frans van Schooten (Młodszy, 1615-1660). Był on holenderskim matematykiem związanym ze szkołą inżynierską w Lejdzie oraz uczniem i przyjacielem René Descartesa (Kartezjusza). W 1637 roku pomagał Kartezjuszowi w przygotowaniu ilustracji do pierwszego wydania traktatu Discours de la méthode..., który zawierał esej La géométrie. W 1649 roku van Schooten przetłumaczył na łacinę i wydał Geometrię Kartezjusza, wraz z licznymi komentarzami i uzupełnieniami (swoimi i swoich uczniów). Van Schooten stał się jednym z pierwszych matematyków promujących i rozpowszechniających nową Geometrię Kartezjusza. Znakomitym uczniem van Schootena był Christiaan Huygens.
Problem ten rozstrzygnął w 1646 roku Frans van Schooten (Młodszy, 1615-1660). Był on holenderskim matematykiem związanym ze szkołą inżynierską w Lejdzie oraz uczniem i przyjacielem René Descartesa (Kartezjusza). W 1637 roku pomagał Kartezjuszowi w przygotowaniu ilustracji do pierwszego wydania traktatu Discours de la méthode..., który zawierał esej La géométrie. W 1649 roku van Schooten przetłumaczył na łacinę i wydał Geometrię Kartezjusza, wraz z licznymi komentarzami i uzupełnieniami (swoimi i swoich uczniów). Van Schooten stał się jednym z pierwszych matematyków promujących i rozpowszechniających nową Geometrię Kartezjusza. Znakomitym uczniem van Schootena był Christiaan Huygens.

Rys. 4.
Rozwiązanie van Schootena jest geometryczne i niezwykle pomysłowe. Niech dany będzie kąt 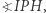 różny od kąta prostego. Po ramionach tego kąta ślizga się odcinek
różny od kąta prostego. Po ramionach tego kąta ślizga się odcinek 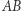 (Rys. 4). Jaką krzywą zakreśla wówczas punkt
(Rys. 4). Jaką krzywą zakreśla wówczas punkt 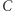 należący do tego odcinka i nie będący jego końcem? Punkty
należący do tego odcinka i nie będący jego końcem? Punkty 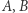 i
i 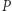 jednoznacznie wyznaczają okrąg o środku
jednoznacznie wyznaczają okrąg o środku 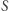 opisany na trójkącie
opisany na trójkącie 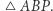 Prosta
Prosta 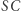 wyznacza średnicę
wyznacza średnicę 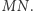 Wówczas proste
Wówczas proste 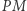 i
i 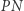 tworzą kąt prosty. Po przemieszczeniu się odcinka
tworzą kąt prosty. Po przemieszczeniu się odcinka  do położenia
do położenia 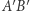 punkty
punkty 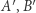 i
i 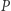 wyznaczają okrąg o środku
wyznaczają okrąg o środku 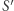 opisany na trójkącie
opisany na trójkącie 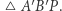 Prosta
Prosta 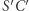 wyznacza jego średnicę
wyznacza jego średnicę 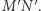 Oczywiście
Oczywiście 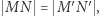 bo utworzone okręgi są przystające (gdyż kąt
bo utworzone okręgi są przystające (gdyż kąt 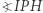 wpisany w oba okręgi wyznacza w nich cięciwy równej długości). Ponadto kąty
wpisany w oba okręgi wyznacza w nich cięciwy równej długości). Ponadto kąty 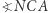 i
i 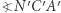 są równe (cięciwy
są równe (cięciwy 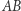 i
i 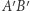 są takiej samej długości, więc ich odległości od środków odpowiednich okręgów pozostają stałe). Analogicznie, kąty
są takiej samej długości, więc ich odległości od środków odpowiednich okręgów pozostają stałe). Analogicznie, kąty 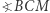 i
i  są równe. W tej sytuacji, dla przystających okręgów łuk
są równe. W tej sytuacji, dla przystających okręgów łuk 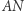 jest takiej samej długości jak łuk
jest takiej samej długości jak łuk 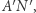 więc kąty wpisane oparte na tych łukach są równe, tj.
więc kąty wpisane oparte na tych łukach są równe, tj.  Ponieważ kąty te leżą po tej samej stronie prostej
Ponieważ kąty te leżą po tej samej stronie prostej 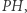 więc punkt
więc punkt  leży na prostej
leży na prostej  Z analogicznych powodów punkt
Z analogicznych powodów punkt 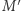 leży na prostej
leży na prostej 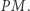 Oznacza to, że ślad punktu
Oznacza to, że ślad punktu 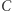 możemy wyznaczyć z ruchu odcinka
możemy wyznaczyć z ruchu odcinka  którego końce ślizgają się po wzajemnie prostopadłych prostych
którego końce ślizgają się po wzajemnie prostopadłych prostych 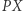 i
i 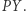 Z wcześniejszych rozważań wiemy już, że w tym przypadku punkt
Z wcześniejszych rozważań wiemy już, że w tym przypadku punkt  zakreśla łuk elipsy. Zatem mamy:
zakreśla łuk elipsy. Zatem mamy:
Twierdzenie (Frans van Schooten (Młodszy), 1646 r.). Jeśli punkty 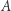 i
i 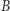 prostej
prostej 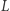 ślizgają się po ramionach kąta
ślizgają się po ramionach kąta 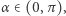 to każdy inny punkt prostej
to każdy inny punkt prostej 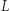 zakreśla elipsę.
zakreśla elipsę.

Rys. 5.

Rys. 6. Każdy trójkąt da się zamieść odcinkiem przy odpowiednim ruchu

Rys. 7.
A może potrafimy coś powiedzieć o obszarach "zakreślanych" przez tak wędrujące odcinki? W Kalejdoskopie matematycznym Hugona Steinhausa wiele wyjaśniają rysunki (Rys. 5, 6) oraz tekst:
Gdy poruszamy zapałkę tak, żeby jej oba końce biegły po prostych przecinających się, to ruch jej jest identyczny z ruchem cięciwy mniejszego koła w systemie 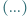 dwóch kół [patrz Rys. 1]. Trzeba tylko wziąć przecięcie prostych za środek dużego koła, a małe koło narysować przez środek dużego i oba końce zapałki.
dwóch kół [patrz Rys. 1]. Trzeba tylko wziąć przecięcie prostych za środek dużego koła, a małe koło narysować przez środek dużego i oba końce zapałki.
Gdy końce odcinka ślizgają się po wzajemnie prostopadłych prostych, to zamiecie on obszar ograniczony asteroidą (Rys. 7).
Z przemieszczaniem odcinka na płaszczyźnie związanych jest wiele ciekawych i niebanalnych zagadnień, np.:
Twierdzenie (Hamnet Holditch, 1858 r.). Jeśli oba końce odcinka ślizgają się po krzywej zamkniętej  a punkt
a punkt 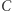 dzielący odcinek w stosunku
dzielący odcinek w stosunku 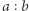 zakreśla krzywą
zakreśla krzywą  to różnica pól figur ograniczonych krzywymi
to różnica pól figur ograniczonych krzywymi  i
i  jest równa
jest równa 
(Patrz Rys. 8 oraz Delta 8/1984, Delta 10/1986.)
Problem (Sōichi Kakeya, 1917 r.). Na płaszczyźnie wyznaczyć zbiór o najmniejszym polu, w którym można odcinek jednostkowy obrócić o kąt co najmniej 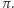
O zmaganiach z tym problemem pisaliśmy też w Delcie 6/1983 i Delcie 4/2013).
Dwa przykłady zbiorów, w których możliwy jest obrót odcinka, pokazano na rysunku 9.


