Sytuację analizujemy z lotu ptaka, czyli szukamy pola powierzchni figury płaskiej. Pierwszym nasuwającym się rozwiązaniem jest sofa w kształcie półkola o promieniu 1 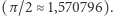W 1968 roku John Hammersley przedstawił rozwiązanie dużo lepsze. Pomysł polegał na wydłużeniu półkola o prostokąt o wymiarach 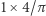z wyciętym mniejszym półkolem o promieniu 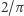(rysunek poniżej z prawej). Tym samym otrzymał rozwiązanie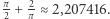

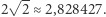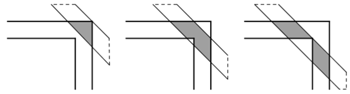
Dodatkowo prostym argumentem uzasadnił, że szukane pole nie może być większe niż Jeden z wymiarów sofy musi mieć, oczywiście, szerokość co najwyżej korytarza (jednostkową). Określając, jakie jest największe pole przecięcia pasa o szerokości 1 z korytarzem, gdy pas jest nachylony do korytarza pod kątem 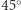(odpowiada to sytuacji, w której sofa znajduje się w "połowie zakrętu"), znajdziemy górne ograniczenie. Największe możliwe przecięcie znajduje się na ostatnim rysunku z prawej i wynosi właśnie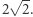

W 1992 roku Joseph Gerver skonstruował sofę o polu 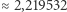i postawił hipotezę, że jest to najlepsze możliwe rozwiązanie. Kontur sofy Hammersleya składa się z trzech odcinków i trzech łuków okręgów, natomiast kontur sofy Gervera - z trzech odcinków i piętnastu łuków.

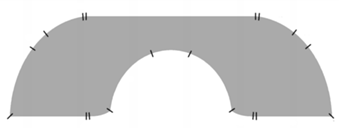
Sofa Gervera

12 lat później Phillip Gibbs rozwiązał dyskretną wersję problemu - zakładał, że kontur sofy ma być zamkniętą łamaną i wykonał kolejne komputerowe iteracje - i otrzymał pole zgodne z rezultatem Gervera do szóstego miejsca po przecinku.

Najnowszy wynik, z 2017 roku, to poprawienie ograniczenia górnego do 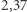. Autorami są Yoav Kallus i Dan Romia i jest to pierwszy rezultat dotyczący ograniczenia górnego od czasów wyniku Hammersleya. Autorzy za pomocą metod numerycznych opracowali algorytm, który dał powyższe oszacowanie po trzech tygodniach pracy komputera (w swoim artykule zaznaczają, że dużo słabsze oszacowanie 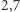można uzyskać w czasie mniejszym niż jedna minuta).

Pytanie, czy pole sofy Gervera jest rzeczywiście największe z możliwych, wciąż pozostaje otwarte.