O ortocentrach i parabolach, a zwłaszcza o twierdzeniu odwrotnym Steinera

Rys. 1
W Delcie 11/2017 został przedstawiony (bez dowodu) fakt, że dla czterech dowolnych prostych (tak dowolnych, że są parami nierównoległe i żadne trzy nie mają punktu wspólnego) ortocentra wyznaczonych przez nie czterech trójkątów leżą na jednej prostej, a okręgi opisane na tych trójkątach mają punkt wspólny. Ponadto parabola, której kierownicą jest prosta zawierająca ortocentra, a ogniskiem punkt wspólny okręgów opisanych jest styczna do czterech wyjściowych prostych (Rys. 1).
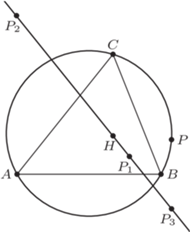
Rys. 2
Z przyczyn dla mnie samego niejasnych ta ciekawostka spowodowała, że - chyba pierwszy raz od matury - pochyliłem się nad planimetrią. W dalszej części można się zapoznać z dowodem, którym zaowocowały moje rozważania. Skorzystamy w nim z następujących twierdzeń, które same w sobie są całkiem interesujące:
Twierdzenie 1 (Steiner). Jeśli punkt  leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie  to odbicia symetryczne punktu
to odbicia symetryczne punktu  względem prostych
względem prostych  i
i  leżą na jednej prostej, przechodzącej przez ortocentrum trójkąta
leżą na jednej prostej, przechodzącej przez ortocentrum trójkąta  (Rys. 2). Prostą tę nazywamy prostą Steinera punktu
(Rys. 2). Prostą tę nazywamy prostą Steinera punktu  w trójkącie
w trójkącie 
Dowód tego twierdzenia został omówiony na łamach Delty w listopadzie 2016 roku. Na potrzeby dalszych rozważań bardziej będzie nam potrzebne twierdzenie odwrotne.
Twierdzenie 2. Dany jest trójkąt  i punkt
i punkt  Jeśli obrazy punktu
Jeśli obrazy punktu  w symetriach względem boków trójkąta
w symetriach względem boków trójkąta 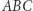 leżą na jednej prostej, wtedy punkt
leżą na jednej prostej, wtedy punkt 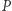 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 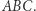 Ponadto prosta zawierająca odbicia symetryczne punktu
Ponadto prosta zawierająca odbicia symetryczne punktu 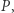 zawiera ortocentrum trójkąta
zawiera ortocentrum trójkąta 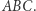
Kolejną wariację na temat twierdzenia Steinera pozwolę sobie nazwać twierdzeniem dualnym, ponieważ zamienia ono niejako rolę prostych i punktów.
Twierdzenie 3. Dany jest trójkąt 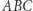 i prosta
i prosta 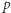 przechodząca przez ortocentrum trójkąta
przechodząca przez ortocentrum trójkąta 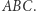 Wtedy odbicia
Wtedy odbicia 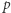 względem boków trójkąta przecinają się w jednym punkcie, leżącym na okręgu opisanym na trójkącie
względem boków trójkąta przecinają się w jednym punkcie, leżącym na okręgu opisanym na trójkącie 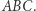
Zanim przejdziemy do dowodów powyższych twierdzeń, przyjrzyjmy się, jak z ich pomocą można udowodnić wyjściowy problem czterech prostych.
Niech 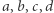 będą czterema danymi prostymi. Niech
będą czterema danymi prostymi. Niech 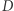 oznacza ortocentrum trójkąta
oznacza ortocentrum trójkąta 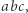 a
a 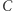 oznacza ortocentrum trójkąta
oznacza ortocentrum trójkąta 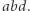 Na mocy Twierdzenia 3 odbicia prostej
Na mocy Twierdzenia 3 odbicia prostej 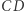 względem prostych
względem prostych 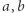 i
i  przecinają się w pewnym punkcie okręgu opisanego na trójkącie
przecinają się w pewnym punkcie okręgu opisanego na trójkącie 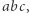 a jej odbicia względem prostych
a jej odbicia względem prostych 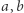 i
i 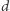 również mają wspólny punkt, leżący na okręgu opisanym na trójkącie
również mają wspólny punkt, leżący na okręgu opisanym na trójkącie 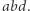 Musi to być ten sam punkt. Nazwijmy go
Musi to być ten sam punkt. Nazwijmy go 
Odbicia punktu 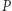 względem prostych
względem prostych 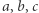 i
i 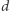 leżą na prostej
leżą na prostej 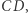 więc (na mocy Twierdzenia 2) punkt ten leży na okręgach opisanych na każdym z trójkątów
więc (na mocy Twierdzenia 2) punkt ten leży na okręgach opisanych na każdym z trójkątów 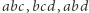 i
i 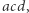 a prosta
a prosta 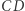 zawiera ortocentra wszystkich tych trójkątów. Związek współliniowości ortocentrów ze wspólnym punktem okręgów opisanych, który został wspomniany w wyjściowym artykule jako podejrzenie/wskazówka, jest wyraźnie widoczny.
zawiera ortocentra wszystkich tych trójkątów. Związek współliniowości ortocentrów ze wspólnym punktem okręgów opisanych, który został wspomniany w wyjściowym artykule jako podejrzenie/wskazówka, jest wyraźnie widoczny.
Teraz należy jeszcze wykazać, że parabola wyznaczona przez ognisko 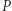 i kierownicę
i kierownicę 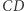 jest styczna do prostych
jest styczna do prostych 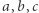 i
i 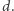 Skorzystamy tu z następującego faktu, którego uzasadnienie można znaleźć w Deltoidzie 6/2018:
Skorzystamy tu z następującego faktu, którego uzasadnienie można znaleźć w Deltoidzie 6/2018:
Lemat (charakteryzacja stycznych do paraboli). Prosta jest styczna do paraboli o ognisku 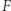 i kierownicy
i kierownicy 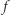 wtedy i tylko wtedy, gdy jest symetralną pewnego odcinka łączącego
wtedy i tylko wtedy, gdy jest symetralną pewnego odcinka łączącego 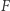 z punktem na
z punktem na 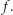
Ponieważ wiemy, że odbicia symetryczne 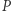 względem prostych
względem prostych 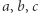 i
i 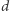 leżą na
leżą na 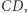 natychmiast otrzymujemy, że
natychmiast otrzymujemy, że  i
i  są styczne do interesującej nas paraboli. Kończy to dowód przytoczonego na wstępie faktu.
są styczne do interesującej nas paraboli. Kończy to dowód przytoczonego na wstępie faktu.
Przedstawione rozumowanie pokazuje w dodatku, że punkt okręgu opisanego i jego prosta Steinera wyznaczają parabolę styczną do prostych zawierających boki trójkąta. Można się zastanowić, czy jest to jednoznaczna charakteryzacja wszystkich takich parabol. Tutaj nie będziemy tego rozważać.
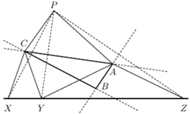
Zaprezentowane rozumowanie może wydawać się zależne od przedstawionej na rysunku konfiguracji punktów. Wykorzystywane równości są jednak prawdziwe nawet jeśli uznamy, że dotyczą kątów skierowanych, co uwalnia nas od potrzeby rozważania przypadków.
Teraz pozostaje już tylko udowodnić twierdzenia 2 i 3. Zaczniemy od dowodu twierdzenia odwrotnego.
Dowód twierdzenia odwrotnego. Niech 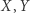 i
i 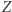 będą odbiciami punktu
będą odbiciami punktu 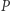 względem prostych, kolejno
względem prostych, kolejno 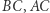 i
i 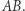 Jeśli
Jeśli 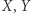 i
i 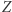 nie są parami różne, punkt
nie są parami różne, punkt  musi pokrywać się z jednym z wierzchołków trójkąta (więc, oczywiście, leży na okręgu opisanym). Podobnie jest w przypadku, gdy
musi pokrywać się z jednym z wierzchołków trójkąta (więc, oczywiście, leży na okręgu opisanym). Podobnie jest w przypadku, gdy 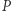 leży na prostej
leży na prostej 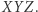 Powinno się to stać jasne, jeśli zauważymy, że trójkąt
Powinno się to stać jasne, jeśli zauważymy, że trójkąt 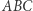 jest wyznaczony przez symetralne odcinków
jest wyznaczony przez symetralne odcinków 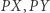 i
i 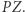 Bez straty ogólności możemy przyjąć, że punkt
Bez straty ogólności możemy przyjąć, że punkt 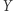 leży pomiędzy
leży pomiędzy 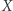 i
i 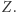 Dowód sprowadza się do przeliczeń na kątach. Na początku zauważamy następujące równości:
Dowód sprowadza się do przeliczeń na kątach. Na początku zauważamy następujące równości:
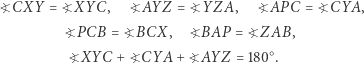 |
Analizując trójkąt wyznaczony przez proste 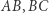 i
i 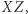 otrzymujemy:
otrzymujemy:

Podstawiając poprzednie równości, otrzymujemy:
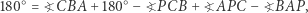 |
zatem 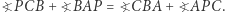 Ostatnia równość oznacza, że czworokąt
Ostatnia równość oznacza, że czworokąt 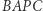 jest wpisany w okrąg, czyli to, co należało wykazać. Dzięki podstawowemu twierdzeniu Steinera prosta zawierająca odbicia symetryczne pewnego punktu z okręgu opisanego względem boków trójkąta przechodzi przez ortocentrum.
jest wpisany w okrąg, czyli to, co należało wykazać. Dzięki podstawowemu twierdzeniu Steinera prosta zawierająca odbicia symetryczne pewnego punktu z okręgu opisanego względem boków trójkąta przechodzi przez ortocentrum.
Na zakończenie udowodnimy twierdzenie dualne.
Dowód twierdzenia dualnego. Odbicia symetryczne prostej przechodzącej przez ortocentrum mają punkty wspólne z okręgiem opisanym (np. odbicia ortocentrum). Zauważmy, że jeśli obraz jest styczną, musi być równoległy do boku trójkąta, a tym samym do wyjściowej prostej. Ta zaś może być równoległa do co najwyżej jednego boku trójkąta, więc przynajmniej dwa jej odbicia nie są stycznymi.
Wiemy zatem, że pewien obraz wyjściowej prostej ma drugi punkt wspólny z okręgiem. Oznaczmy ten punkt przez 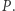 Prosta Steinera punktu
Prosta Steinera punktu 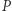 musi być wyjściową prostą, ponieważ ma z nią co najmniej dwa punkty wspólne (ortocentrum i pewne odbicie
musi być wyjściową prostą, ponieważ ma z nią co najmniej dwa punkty wspólne (ortocentrum i pewne odbicie  ).
).
To kończy dowód, ponieważ każdy punkt okręgu opisanego leży na odbiciu symetrycznym swojej prostej Steinera względem dowolnego boku trójkąta.
Miło jest czasem powrócić do geometrii.