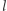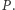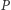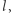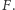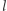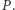Deltoid
Odbicia w paraboli
Tym razem o paraboli...
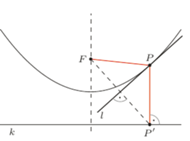
Rys. 1
Parabola to zbiór punktów płaszczyzny równo odległych od ustalonego punktu 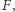 zwanego ogniskiem, i od ustalonej nieprzechodzącej przez
zwanego ogniskiem, i od ustalonej nieprzechodzącej przez 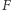 prostej
prostej 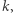 zwanej kierownicą (Rys. 1). Z definicji tej wynika, że parabola ma oś symetrii przechodzącą przez ognisko i prostopadłą do kierownicy oraz że wszystkie punkty paraboli leżą w tej półpłaszczyźnie wyznaczonej przez kierownicę, do której należy ognisko.
zwanej kierownicą (Rys. 1). Z definicji tej wynika, że parabola ma oś symetrii przechodzącą przez ognisko i prostopadłą do kierownicy oraz że wszystkie punkty paraboli leżą w tej półpłaszczyźnie wyznaczonej przez kierownicę, do której należy ognisko.
Styczna do paraboli to taka prosta, która ma z nią dokładnie jeden punkt wspólny, a wszystkie inne punkty paraboli znajdują się po jednej stronie tej prostej.
Fakt. Każdy punkt 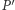 z kierownicy jest rzutem dokładnie jednego punktu
z kierownicy jest rzutem dokładnie jednego punktu 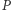 paraboli (należącego do symetralnej odcinka
paraboli (należącego do symetralnej odcinka 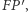 wówczas
wówczas 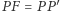 ).
).
Rozważmy dowolny punkt 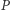 paraboli, jego rzut
paraboli, jego rzut 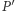 na kierownicę
na kierownicę 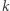 oraz prostą
oraz prostą 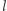 zawierającą dwusieczną kąta
zawierającą dwusieczną kąta 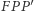 (Rys. 1). Z definicji paraboli
(Rys. 1). Z definicji paraboli 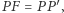 więc prosta
więc prosta 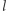 jest też symetralną odcinka
jest też symetralną odcinka 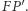 Wykażemy, że
Wykażemy, że 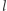 jest styczną.
jest styczną.
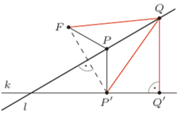
Rys. 2
Dowód. Przypuśćmy, że do prostej 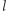 należy jeszcze jakiś punkt paraboli
należy jeszcze jakiś punkt paraboli 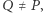 niech
niech 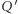 będzie jego rzutem na
będzie jego rzutem na 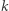 (Rys. 2). Wówczas
(Rys. 2). Wówczas 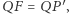 bo
bo 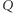 leży na symetralnej
leży na symetralnej 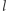 odcinka
odcinka 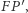 a także
a także 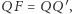 bo
bo 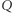 należy do paraboli. Zatem
należy do paraboli. Zatem 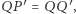 czyli
czyli 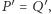 sprzecznie z faktem powyżej.
sprzecznie z faktem powyżej.
Dowód. Przypuśćmy, że jakiś punkt 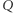 paraboli leży po przeciwnej stronie
paraboli leży po przeciwnej stronie 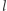 niż
niż 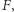 niech
niech 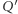 będzie jego rzutem na
będzie jego rzutem na 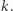 Wówczas, kolejno z własności symetralnej i rzutu, uzyskujemy
Wówczas, kolejno z własności symetralnej i rzutu, uzyskujemy 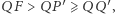 sprzecznie z definicją paraboli.
sprzecznie z definicją paraboli.
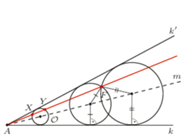
Rys. 3
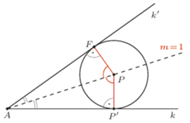
Rys. 4
Dowód. Rozważmy prostą  przez
przez 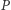 dla
dla 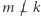 oraz
oraz 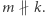 Niech
Niech 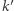 - obraz
- obraz 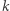 w symetrii względem
w symetrii względem 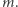 Oznaczmy przez
Oznaczmy przez 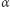 ten z kątów utworzonych przez
ten z kątów utworzonych przez 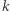 i
i 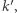 który zawiera
który zawiera 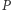 (
( 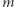 jest jego dwusieczną), wierzchołek
jest jego dwusieczną), wierzchołek 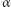 nazwijmy
nazwijmy 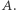
Wtedy 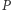 leży na dwusiecznej
leży na dwusiecznej 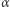 i
i 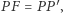 więc
więc 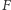 nie może leżeć na zewnątrz
nie może leżeć na zewnątrz 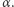
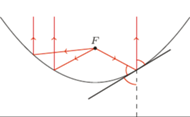
Rys. 5
Jeśli 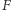 leży wewnątrz
leży wewnątrz 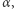 to półprosta
to półprosta 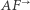 przecina okrąg
przecina okrąg 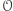 wpisany w kąt
wpisany w kąt 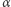 w dwóch punktach
w dwóch punktach 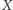 i
i 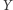 (Rys. 3). Jednokładności o środku
(Rys. 3). Jednokładności o środku 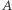 przekształcające
przekształcające 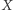 na
na 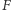 i
i 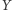 na
na 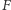 przeprowadzają
przeprowadzają 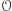 na dwa różne okręgi wpisane w
na dwa różne okręgi wpisane w 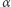 i przechodzące przez
i przechodzące przez 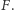 Ich środki leżą na
Ich środki leżą na 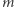 i są tak samo odległe od
i są tak samo odległe od 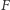 jak od
jak od 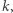 więc leżą też na paraboli. Wobec tego
więc leżą też na paraboli. Wobec tego 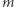 nie jest do niej styczna.
nie jest do niej styczna.
Jeśli 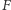 leży na
leży na 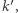 to istnieje jedyny okrąg wpisany w
to istnieje jedyny okrąg wpisany w 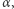 przechodzący przez
przechodzący przez 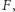 więc jego środek
więc jego środek 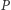 to jedyny punkt
to jedyny punkt 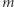 należący do paraboli. Wówczas
należący do paraboli. Wówczas  zawiera dwusieczną kąta
zawiera dwusieczną kąta 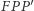 (Rys. 4), czyli
(Rys. 4), czyli 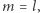 co kończy dowód.
co kończy dowód.
Wniosek. Z równości kątów przy dwusiecznej 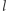 (Rys. 5) wynika, iż promienie światła wychodzące z ogniska i odbijające się od lustrzanej paraboli wedle reguły kąt padania równy jest kątowi odbicia wędrują dalej jako wiązka równoległa do osi symetrii. Również na odwrót, wiązka promieni równoległych do osi symetrii po odbiciu skupia się w ognisku. Tak samo jest dla trójwymiarowej paraboloidy otrzymanej przez obrócenie paraboli wokół jej osi symetrii.
(Rys. 5) wynika, iż promienie światła wychodzące z ogniska i odbijające się od lustrzanej paraboli wedle reguły kąt padania równy jest kątowi odbicia wędrują dalej jako wiązka równoległa do osi symetrii. Również na odwrót, wiązka promieni równoległych do osi symetrii po odbiciu skupia się w ognisku. Tak samo jest dla trójwymiarowej paraboloidy otrzymanej przez obrócenie paraboli wokół jej osi symetrii.

Korzystając z opisanej własności rozpala się ogień olimpijski (ilustracja 3 na tylnej okładce), gotuje (9) i topi metale w temperaturze 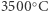 (2). Kształt wycinka paraboloidy mają anteny satelitarne, mogą one być ustawiane pionowo, a ognisko nie musi być nad środkiem talerza (4). Są też teleskopy z płynnym lustrem z rtęci, przybierającym kształt paraboloidy wskutek kręcenia się ze stałą prędkością wokół swej osi - te z kolei mogą być tylko skierowane w górę (5). Własności paraboloid stosuje się w mikrofonach szpiegowskich i ornitologicznych (1), konstrukcje o zbliżonym kształcie służyły też w Anglii w czasie I Wojny Światowej do nasłuchiwania, czy nadlatują niemieckie sterowce z bombami (7). Dwa paraboloidalne talerze ustawione naprzeciw siebie umożliwiają szeptanie na odległość (6). Na podobnej zasadzie powstaje iluzja monety leżącej na górze "ufo" (10) - w rzeczywistości moneta ta leży na dnie paraboloidalnej lustrzanej miseczki (8).
(2). Kształt wycinka paraboloidy mają anteny satelitarne, mogą one być ustawiane pionowo, a ognisko nie musi być nad środkiem talerza (4). Są też teleskopy z płynnym lustrem z rtęci, przybierającym kształt paraboloidy wskutek kręcenia się ze stałą prędkością wokół swej osi - te z kolei mogą być tylko skierowane w górę (5). Własności paraboloid stosuje się w mikrofonach szpiegowskich i ornitologicznych (1), konstrukcje o zbliżonym kształcie służyły też w Anglii w czasie I Wojny Światowej do nasłuchiwania, czy nadlatują niemieckie sterowce z bombami (7). Dwa paraboloidalne talerze ustawione naprzeciw siebie umożliwiają szeptanie na odległość (6). Na podobnej zasadzie powstaje iluzja monety leżącej na górze "ufo" (10) - w rzeczywistości moneta ta leży na dnie paraboloidalnej lustrzanej miseczki (8).