Deltoid
Wysokości czworokąta
Wysokością czworokąta nazwijmy prostą przechodzącą przez środek jego boku i prostopadłą do boku przeciwległego. W niektórych czworokątach wszystkie cztery wysokości przecinają się w jednym punkcie - ortocentrum czworokąta. Przykładowo kwadrat ma ortocentrum, a romb niebędący kwadratem nie ma.
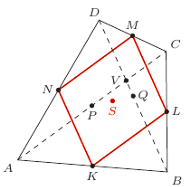
Rys. 1. 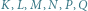 są środkami odpowiednich boków i przekątnych.
są środkami odpowiednich boków i przekątnych.
Rys. 2.  - ortocentrum czworokąta.
- ortocentrum czworokąta.
Rozważmy czworokąt 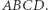 Przyjmijmy oznaczenia jak na rysunkach 1 i 2.
Przyjmijmy oznaczenia jak na rysunkach 1 i 2.
Lemat. 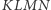 to równoległobok, a jego środek
to równoległobok, a jego środek  jest też środkiem odcinka
jest też środkiem odcinka 
W dowodzie można wykorzystać np. linię środkową (deltoid 5/2017) lub środki ciężkości (deltoid 12/2011), a przy okazji wykazać, że punkt 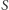 jest środkiem ciężkości układu punktów
jest środkiem ciężkości układu punktów 
Twierdzenie. Czworokąt ma ortocentrum wtedy i tylko wtedy, gdy można na nim opisać okrąg.
Dowód. Na mocy lematu, symetria środkowa względem 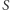 przeprowadza punkt
przeprowadza punkt  na
na 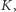 a wysokość z
a wysokość z 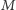 na prostą przez
na prostą przez 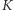 i prostopadłą do
i prostopadłą do 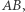 czyli na symetralną boku
czyli na symetralną boku 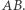 Analogicznie obrazami pozostałych wysokości są odpowiednie symetralne boków. Wobec tego ortocentrum czworokąta istnieje wtedy i tylko wtedy, gdy istnieje wspólny punkt symetralnych jego boków, czyli środek okręgu opisanego.
Analogicznie obrazami pozostałych wysokości są odpowiednie symetralne boków. Wobec tego ortocentrum czworokąta istnieje wtedy i tylko wtedy, gdy istnieje wspólny punkt symetralnych jego boków, czyli środek okręgu opisanego.
Wniosek. Punkty 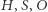 leżą na jednej prostej, w tej kolejności i
leżą na jednej prostej, w tej kolejności i 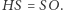
W zadaniach 1, 2, 4 i 5 zakładamy, że czworokąt 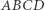 ma ortocentrum.
ma ortocentrum.
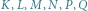 są środkami odpowiednich boków i przekątnych.
są środkami odpowiednich boków i przekątnych.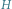 - ortocentrum czworokąta.
- ortocentrum czworokąta.