Tak samo, ale zupełnie inaczej
Geometrzy od dawna marzyli o współrzędnych jednorodnych, czyli takich 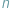 -tkach liczb (dalej dla uproszczenia będzie mowa o parach i trójkach) przyporządkowanych punktom, że gdy wszystkie liczby w
-tkach liczb (dalej dla uproszczenia będzie mowa o parach i trójkach) przyporządkowanych punktom, że gdy wszystkie liczby w 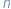 -tce pomnożymy przez tę samą liczbę, to nowa
-tce pomnożymy przez tę samą liczbę, to nowa 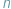 -tka będzie współrzędnymi tego samego punktu.
-tka będzie współrzędnymi tego samego punktu.
Traci się w ten sposób jednoznaczność współrzędnych danego punktu, ale zyskuje się to, że wszelkie sytuacje geometryczne będą opisywane wyłącznie funkcjami jednorodnymi. To wielka wygoda, bo okazuje się, że dla 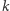 naturalnych
naturalnych
funkcja jednorodna w stopniu 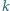 i gładka w stopniu
i gładka w stopniu 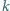 to zawsze wielomian.
to zawsze wielomian.
Dowód tego faktu jest bardzo prosty (Euler), ale wymaga - rzecz jasna - użycia pojęcia pochodnej, więc go pominę.
Aby ten cel osiągnąć, Julius Plücker zaproponował współrzędne trójkątowe zwane też trójliniowymi.
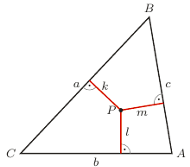
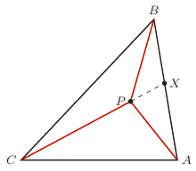
Rys. 1
Jak się łatwo domyślić, potrzebny jest w tym celu trójkąt, ale trójkąt, w którym dysponujemy całymi prostymi zawierającymi jego boki. Współrzędne punktu to będą odległości od tych prostych, przy czym odległość będziemy brali ze znakiem " 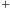 ", gdy punkt leży po tej samej stronie prostej, co nieleżący na niej wierzchołek trójkąta, i ze znakiem "
", gdy punkt leży po tej samej stronie prostej, co nieleżący na niej wierzchołek trójkąta, i ze znakiem "  " w przeciwnym przypadku.
" w przeciwnym przypadku.
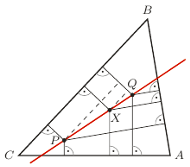
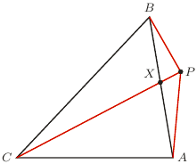
Rys. 2
Jak widać, na rysunku 1 punkt 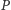 ma wszystkie współrzędne dodatnie. Takimi też będę się posługiwał, pozostawiając Czytelnikowi (łatwe) rozpatrzenie innych przypadków.
ma wszystkie współrzędne dodatnie. Takimi też będę się posługiwał, pozostawiając Czytelnikowi (łatwe) rozpatrzenie innych przypadków.
Oznaczmy pole trójkąta 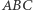 przez
przez 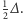 Współrzędnymi
Współrzędnymi 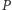 jest więc trójka
jest więc trójka 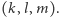 Zauważmy też, że
Zauważmy też, że

To proste spostrzeżenie pozwala potwierdzić, że współrzędne te są faktycznie jednorodne, bo jednostki miar długości czy pola możemy dobrać dowolnie.
Zaletą dodatkową współrzędnych trójkątowych jest to, iż proste mają w tych współrzędnych równania liniowe. Sprawdźmy to.
Niech współrzędnymi 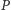 będzie trójka
będzie trójka 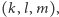 a współrzędnymi
a współrzędnymi 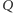 trójka
trójka 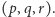 Znajdźmy warunek na to, by punkt
Znajdźmy warunek na to, by punkt 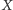 o współrzędnych
o współrzędnych 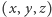 leżał na prostej
leżał na prostej 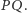
Z rysunku 2 mamy

Podobnie


Rudolph Hoffmann
Julius Plücker (1801-1868)

Adolf Neumann
Ferdinand Möbius (1790-1868)
Teraz potrzebna nam będzie trójka 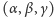 spełniająca dwa warunki
spełniająca dwa warunki

Takie warunki użytkownicy algebry liniowej nazywają znikaniem iloczynu skalarnego, a poszukiwana trójka to dla nich iloczyn wektorowy. Nie trzeba jednak tych pojęć znać, by sprawdzić poprawność zgadniętej odpowiedzi.
Taką trójką jest 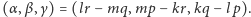 Z udowodnionych wyżej proporcji mamy więc
Z udowodnionych wyżej proporcji mamy więc 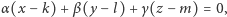 a na koniec
a na koniec 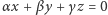 - i takie jest równanie prostej
- i takie jest równanie prostej 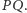
Bardzo ładnie, ale co z tego za pożytek?
Aby go zobaczyć, trzeba spojrzeć na to oczyma kolegi Plückera (to nie żart: byli rówieśnikami i bliskimi znajomymi), Ferdinanda Möbiusa.
Möbius postanowił zamiast korzystać z boków trójkąta skorzystać z jego wierzchołków. Co więcej, odwołał się do fizyki, a konkretnie użył środków ciężkości. Już od czasów Archimedesa wiadomo, że grawitacja działa tak "w dół", jak "do góry" (balony, statki na wodzie). Dlatego mamy do czynienia z ciężarami i wyporami, co w szkolnej fizyce prowadzi do pojęcia dźwigni jedno- bądź dwustronnej.
Gdy obciążymy dwa punkty 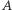 i
i 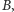 to ich środek ciężkości może wypaść w dowolnym punkcie prostej
to ich środek ciężkości może wypaść w dowolnym punkcie prostej 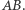 Dokładniej - obowiązuje zasada "ramię razy siła", czyli gdy w punkcie
Dokładniej - obowiązuje zasada "ramię razy siła", czyli gdy w punkcie 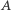 umieścimy ciężar/wypór
umieścimy ciężar/wypór 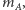 a
a 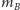 w punkcie
w punkcie 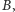 wówczas środek ciężkości będzie spełniał warunek
wówczas środek ciężkości będzie spełniał warunek 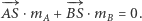 Możemy parę
Możemy parę 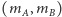 uznać za współrzędne punktu
uznać za współrzędne punktu 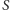 na prostej
na prostej 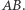 Takie współrzędne Möbius nazwał współrzędnymi barycentrycznymi. Czytelnik zechce sprawdzić, że współrzędne punktów na poniższym rysunku poniżej mogą być następujące:
Takie współrzędne Möbius nazwał współrzędnymi barycentrycznymi. Czytelnik zechce sprawdzić, że współrzędne punktów na poniższym rysunku poniżej mogą być następujące: 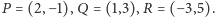 Mogą, bo współrzędne barycentryczne są jednorodne - przecież obciążać punkty możemy równie dobrze w gramach, jak w tonach.
Mogą, bo współrzędne barycentryczne są jednorodne - przecież obciążać punkty możemy równie dobrze w gramach, jak w tonach.

Aby wprowadzić współrzędne barycentryczne na płaszczyźnie, trzeba na niej wskazać odpowiednik zasady "ramię razy siła". A oto i on
Jeśli środkiem ciężkości 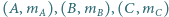 jest punkt
jest punkt 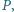 to
to 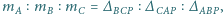 gdzie
gdzie 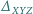 to pole trójkąta
to pole trójkąta 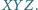
Rzeczywiście, mamy bowiem (Rys. 3)

Równość pozostałych stosunków uzasadniamy analogicznie.
Kolejność wierzchołków przy "deltach" jest pomyślana tak, by rachunek przebiegał równie dobrze dla punktów leżących poza wnętrzem trójkąta 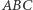 (Rys. 4) - trzeba tylko zamienić pojęcie pola na pojęcie pola zorientowanego, czyli wyróżnić jeden sposób obiegania wierzchołków trójkąta (np. "zgodnie z ruchem wskazówek zegara", czyli ruchem Słońca na naszym niebie) i uznać pola obiegane w ten sposób za dodatnie, a pozostałe za ujemne.
(Rys. 4) - trzeba tylko zamienić pojęcie pola na pojęcie pola zorientowanego, czyli wyróżnić jeden sposób obiegania wierzchołków trójkąta (np. "zgodnie z ruchem wskazówek zegara", czyli ruchem Słońca na naszym niebie) i uznać pola obiegane w ten sposób za dodatnie, a pozostałe za ujemne.
Teraz obciążenia wierzchołków trójkąta odpowiadające punktowi 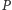 możemy uznać za jego współrzędne barycentryczne.
możemy uznać za jego współrzędne barycentryczne.
I tu warto porównać rysunki 1 i 3 - przecież w obu zainteresowanie skoncentrowane jest na polach trójkątów 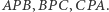 Po chwili zastanowienia dochodzimy do wniosku, że Plücker i Möbius wymyślili to samo, a tylko inaczej na to spojrzeli.
Po chwili zastanowienia dochodzimy do wniosku, że Plücker i Möbius wymyślili to samo, a tylko inaczej na to spojrzeli.
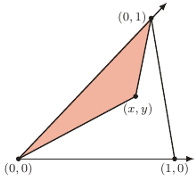
Co więcej, wymyślone przez nich współrzędne są w doskonałej zgodności ze zwykłymi współrzędnymi kartezjańskimi. Uzasadnienie tego jest na rysunku 5
Punkty 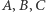 potraktujmy jak wyznaczające kartezjański układ współrzędnych punkty
potraktujmy jak wyznaczające kartezjański układ współrzędnych punkty 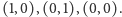 Rozpatrzmy, jak trzeba obciążyć te punkty, by środek ciężkości wypadł w punkcie o kartezjańskich współrzędnych
Rozpatrzmy, jak trzeba obciążyć te punkty, by środek ciężkości wypadł w punkcie o kartezjańskich współrzędnych 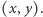 Ze współrzędnych barycentrycznych tego punktu wybierzmy te, które sumują się do 1 (wystarczy podzielić każdą ze współrzędnych przez ich sumę - o ile jest niezerowa) - takie szczególne współrzędne nazywają się arealne. Czytelnik z łatwością zauważy, że obciążenie punktu
Ze współrzędnych barycentrycznych tego punktu wybierzmy te, które sumują się do 1 (wystarczy podzielić każdą ze współrzędnych przez ich sumę - o ile jest niezerowa) - takie szczególne współrzędne nazywają się arealne. Czytelnik z łatwością zauważy, że obciążenie punktu 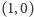 to właśnie będzie
to właśnie będzie 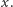 Podobnie
Podobnie 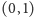 należy obciążyć ciężarem/wyporem
należy obciążyć ciężarem/wyporem 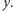 No, a
No, a 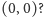 Oczywiście,
Oczywiście, 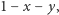 bo to współrzędne arealne, czyli sumujące się do 1.
bo to współrzędne arealne, czyli sumujące się do 1.

Dziś monografia Plückera Analytisch-geometrische Entwicklungen jest praktycznie zapomniana, natomiast dzieło Möbiusa Der barycentrische Calcul cieszy się znacznym szacunkiem. Powód jest niebagatelny, a da się pokazać już w przypadku współrzędnych na prostej: punktu o współrzędnych barycentrycznych 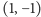 na prostej nie ma! Bo gdy znaki są różne, punkt leży poza odcinkiem
na prostej nie ma! Bo gdy znaki są różne, punkt leży poza odcinkiem 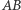 z tej strony, z której wartość bezwzględna obciążenia jest większa (proszę porównać z rysunkiem na górze strony!), a tutaj... Podobnie nie ma na płaszczyźnie punktów, których suma współrzędnych barycentrycznych znika.
z tej strony, z której wartość bezwzględna obciążenia jest większa (proszę porównać z rysunkiem na górze strony!), a tutaj... Podobnie nie ma na płaszczyźnie punktów, których suma współrzędnych barycentrycznych znika.
I Möbius zaproponował, by płaszczyznę (prostą, przestrzeń) uzupełnić o te punkty. I tak wskazał, że jego współrzędne stosują się także w geometrii rzutowej (bo tak nazywają się pouzupełniane w ten sposób przestrzenie różnego wymiaru), a geometria rzutowa to , jak za Cayleyem mówią do dziś geometrzy, cała geometria.