Przesuwanie w zadaniach olimpijskich
W tym artykule omówimy pewną bardzo pożyteczną technikę - tzw. przesuwanie. Polega ona na tym, że niektóre obiekty przesuwamy o pewien wektor i udowadniamy, że teza zadania jest niezmiennicza ze względu na wykonanie tej operacji. Ta metoda pozwala na sprowadzenie rozwiązywanego zadania do znacznie prostszego. Bardzo często ten prostszy przypadek ma jakiś rodzaj symetrii, z której łatwo wywnioskować tezę. Zanim przejdziemy do rozwiązywania zadań, odnotujmy dwie proste własności opisanej operacji.
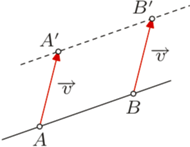
Rys. 1
Własność 1. Jeśli punkty  i
i  przesuniemy o wektor
przesuniemy o wektor  otrzymując punkty
otrzymując punkty 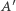 i
i 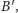 to przesunięcie prostej
to przesunięcie prostej 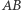 o wektor
o wektor 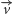 da nam w rezultacie prostą
da nam w rezultacie prostą 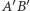 (Rys. 1).
(Rys. 1).
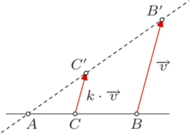
Rys. 2
Własność 2. Dane są punkty  i
i  oraz taki punkt
oraz taki punkt 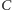 na prostej
na prostej 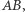 że
że 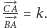 Jeśli punkt
Jeśli punkt 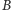 przesuniemy o wektor
przesuniemy o wektor  otrzymując punkt
otrzymując punkt 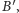 a punkt
a punkt 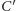 na prostej
na prostej 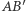 spełnia
spełnia 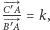 to
to 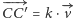 (Rys. 2).
(Rys. 2).
Łatwe dowody powyższych własności pozostawiamy Czytelnikowi. Zauważmy w szczególności, że z drugiej własności wynika, iż środek odcinka 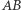 przesunie się o wektor
przesunie się o wektor 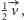 zaś punkt symetryczny do
zaś punkt symetryczny do 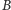 względem punktu
względem punktu 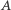 o wektor
o wektor 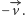
Uzbrojeni w tytułową metodę i powyższe własności możemy przejść do rozwiązania kilku przykładów.
Przykład 1 (Twierdzenie Hjelmsleva). Dane są dwa odcinki 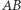 i
i 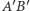 jednakowej długości. Punkty
jednakowej długości. Punkty 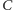 i
i 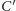 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach  i
i  przy czym
przy czym 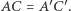 Udowodnić, że środki odcinków
Udowodnić, że środki odcinków 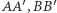 i
i 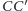 leżą na jednej prostej.
leżą na jednej prostej.
Rozwiązanie. Jeśli przesuniemy odcinek 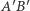 o pewien wektor
o pewien wektor 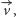 to punkt
to punkt  także przesunie się o wektor
także przesunie się o wektor 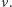 Ponadto środki odcinków
Ponadto środki odcinków 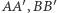 i
i 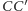 przesuną się o wektor
przesuną się o wektor  Zatem operacja przesuwania nie wpływa na prawdziwość tezy.
Zatem operacja przesuwania nie wpływa na prawdziwość tezy.
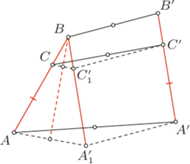
Rys. 3
Przesuńmy zatem odcinek 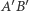 o wektor
o wektor 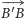 (Rys. . 3). Obrazem punktu
(Rys. . 3). Obrazem punktu 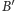 jest, oczywiście, punkt
jest, oczywiście, punkt 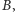 zaś niech
zaś niech 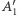 i
i  będą obrazami odpowiednio punktów
będą obrazami odpowiednio punktów 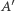 i
i  w tym przesunięciu. Wystarczy udowodnić, że punkt
w tym przesunięciu. Wystarczy udowodnić, że punkt 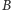 oraz środki odcinków
oraz środki odcinków  i
i 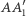 są współliniowe. Jednakże z równości
są współliniowe. Jednakże z równości

i twierdzenia Talesa wynika, że odcinki 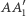 i
i 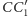 są równoległe, a więc ich środki leżą na środkowej trójkąta
są równoległe, a więc ich środki leżą na środkowej trójkąta 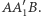
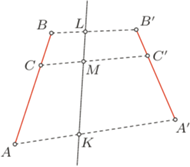
Rys. 4
Nietrudno zauważyć, że opisaną metodą można rozwiązać zadanie ogólniejsze.
Zadanie. Dane są dwa odcinki 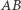 i
i 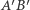 (Rys. 4). Punkty
(Rys. 4). Punkty 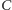 i
i 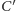 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 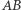 i
i 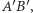 przy czym
przy czym

Niech  będą takimi punktami leżącymi odpowiednio na odcinkach
będą takimi punktami leżącymi odpowiednio na odcinkach 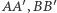 i
i 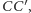 że
że

Wykazać, że punkty 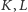 i
i 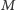 leżą na jednej prostej.
leżą na jednej prostej.
Przejdźmy teraz do następnego przykładu.
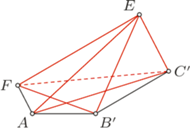
Przykład 2 (III ETAP 57 OM). Dany jest sześciokąt wypukły 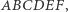 w którym
w którym 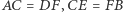 oraz
oraz 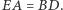 Dowieść, że proste łączące środki przeciwległych boków tego sześciokąta przecinają się w jednym punkcie.
Dowieść, że proste łączące środki przeciwległych boków tego sześciokąta przecinają się w jednym punkcie.
Rozwiązanie. Zauważmy, że jeśli przesuniemy trójkąt 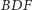 o wektor
o wektor 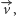 to środki wszystkich boków sześciokąta
to środki wszystkich boków sześciokąta 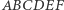 przesuną się o wektor
przesuną się o wektor 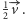 W takim razie każda z rozważanych w treści zadania prostych przesunie się także o wektor
W takim razie każda z rozważanych w treści zadania prostych przesunie się także o wektor 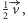 więc teza zadania jest niezmiennicza ze względu na tę operację.
więc teza zadania jest niezmiennicza ze względu na tę operację.
Rys. 5
Skoro trójkąty  i
i 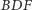 są przystające, to mają jednakowe okręgi opisane (Rys. 5). Przesuńmy więc tak trójkąt
są przystające, to mają jednakowe okręgi opisane (Rys. 5). Przesuńmy więc tak trójkąt 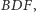 aby rozważane okręgi pokryły się. Niech
aby rozważane okręgi pokryły się. Niech 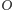 będzie środkiem okręgu opisanego na trójkącie
będzie środkiem okręgu opisanego na trójkącie 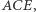 zaś
zaś  obrazem trójkąta
obrazem trójkąta  w tym przesunięciu. Wystarczy udowodnić, że każda z prostych łączących środki przeciwległych boków sześciokąta
w tym przesunięciu. Wystarczy udowodnić, że każda z prostych łączących środki przeciwległych boków sześciokąta 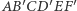 przechodzi przez punkt
przechodzi przez punkt 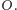
Skoro 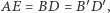 to czworokąt
to czworokąt 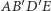 jest trapezem równoramiennym o podstawach
jest trapezem równoramiennym o podstawach 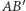 i
i 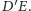 Prosta łącząca środki boków
Prosta łącząca środki boków 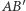 i
i 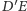 jest jego osią symetrii, a więc na niej musi leżeć środek okręgu opisanego na tym trapezie, czyli punkt
jest jego osią symetrii, a więc na niej musi leżeć środek okręgu opisanego na tym trapezie, czyli punkt 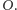 Analogicznie dowodzimy, że punkt
Analogicznie dowodzimy, że punkt 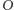 należy do dwóch pozostałych prostych łączących środki przeciwległych boków sześciokąta
należy do dwóch pozostałych prostych łączących środki przeciwległych boków sześciokąta 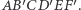
W kolejnym przykładzie przekonamy się, że metoda przesuwania może być także skuteczna w zadaniach o polach.
Przykład 3. W sześciokącie wypukłym 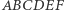 przeciwległe boki są równoległe. Udowodnić, że trójkąty
przeciwległe boki są równoległe. Udowodnić, że trójkąty 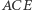 i
i 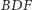 mają równe pola.
mają równe pola.
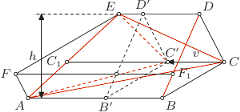
Rys. 6
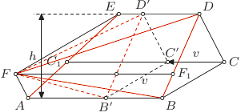
Rys. 7
Rozwiazanie. Wykażemy najpierw, że przesuwanie trójkąta  o wektor
o wektor 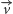 równoległy do boków
równoległy do boków  i
i 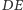 nie ma wpływu na prawdziwość tezy (Rys. 6 i Rys. 7). Niech bowiem
nie ma wpływu na prawdziwość tezy (Rys. 6 i Rys. 7). Niech bowiem 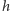 będzie odległością między prostymi
będzie odległością między prostymi 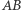 i
i 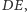 zaś
zaś 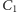 i
i 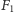 takimi punktami odpowiednio na bokach
takimi punktami odpowiednio na bokach 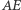 i
i 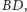 że proste
że proste 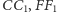 są równoległe do prostej
są równoległe do prostej  Wtedy przed przesunięciem mamy
Wtedy przed przesunięciem mamy

zaś po przesunięciu oba pola wynoszą odpowiednio

albo

Innymi słowy, podczas opisanej operacji oba pola zmieniają się o jednakową wielkość, a więc są równe przed przesunięciem wtedy i tylko wtedy, gdy są równe po przesunięciu.
Rys. 8
Przyjmijmy bez straty dla ogólności, że 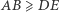 i przesuńmy trójkąt
i przesuńmy trójkąt 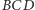 o wektor
o wektor  otrzymując w wyniku trójkąt
otrzymując w wyniku trójkąt 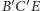 (Rys. 8). Wobec obserwacji poczynionej w pierwszym akapicie wystarczy udowodnić, że trójkąty
(Rys. 8). Wobec obserwacji poczynionej w pierwszym akapicie wystarczy udowodnić, że trójkąty  i
i 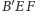 mają równe pola. Ponieważ przesunięcie zachowuje równoległość, to mamy
mają równe pola. Ponieważ przesunięcie zachowuje równoległość, to mamy

W takim razie

Powyższe rozumowanie pozostaje, oczywiście, prawdziwe, gdy punkty  i
i  pokrywają się.
pokrywają się.
Opisane rozwiązanie można dokończyć, inaczej wykonując jeszcze raz operacje z pierwszego akapitu rozwiązania, uzyskując trapez.
Ostatni nasz przykład dotyczy sumy długości odcinków.
Przykład 4 (I etap 52 OM). Okrąg dzieli każdy bok rombu na 3 odcinki. Malujemy otrzymane odcinki kolejno na czerwono, zielono i biało, zaczynając od wierzchołka rombu i poruszając się po jego obwodzie w ustalonym kierunku. Wykazać, że suma długości odcinków czerwonych jest równa sumie długości odcinków białych.

Rys. 9
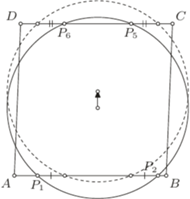
Rys. 10
Rozwiazanie. Niech  będzie danym rombem. Oznaczmy przez
będzie danym rombem. Oznaczmy przez 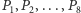 kolejne punkty przecięcia danego okręgu z bokami rombu. Należy wykazać, że
kolejne punkty przecięcia danego okręgu z bokami rombu. Należy wykazać, że

albo

Jeśli przesuniemy dany okrąg o pewien wektor 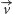 równoległy do boku
równoległy do boku 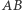 (Rys. 9), to odcinki
(Rys. 9), to odcinki 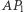 i
i 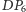 wzrosną o
wzrosną o 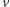 (albo zmaleją, jeśli zwrot był przeciwny do zwrotu wektora
(albo zmaleją, jeśli zwrot był przeciwny do zwrotu wektora 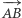 ), zaś odcinki
), zaś odcinki 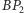 i
i 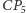 zmaleją o
zmaleją o 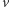 (albo wzrosną, jeśli zwrot był przeciwny do zwrotu wektora
(albo wzrosną, jeśli zwrot był przeciwny do zwrotu wektora  ). W takim razie przy takiej operacji liczba
). W takim razie przy takiej operacji liczba  nie zmienia się. Jeśli teraz przesuniemy dany okrąg o pewien wektor
nie zmienia się. Jeśli teraz przesuniemy dany okrąg o pewien wektor 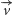 prostopadły do boku
prostopadły do boku 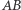 (Rys. 10), to odcinki
(Rys. 10), to odcinki 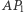 i
i 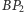 wzrosną o pewną wartość, zaś odcinki
wzrosną o pewną wartość, zaś odcinki 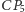 i
i 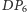 zmaleją o pewną wartość (lub na odwrót w obu przypadkach, gdy zwrot wektora jest w kierunku
zmaleją o pewną wartość (lub na odwrót w obu przypadkach, gdy zwrot wektora jest w kierunku 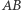 ). Zatem i w tym przypadku liczba
). Zatem i w tym przypadku liczba  nie zmieni się. Skoro dowolny wektor można przedstawić w postaci sumy wektora równoległego do
nie zmieni się. Skoro dowolny wektor można przedstawić w postaci sumy wektora równoległego do 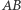 i prostopadłego do
i prostopadłego do 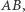 to przesuwanie danego okręgu nie zmienia wartości sumy
to przesuwanie danego okręgu nie zmienia wartości sumy 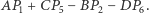 To samo dotyczy sumy
To samo dotyczy sumy 
Przesuńmy zatem tak dany okrąg, aby jego środek pokrył się ze środkiem danego rombu. Wobec poprzednich rozważań wystarczy dowieść tezy w tym przypadku. To jednak natychmiast wynika z symetrii problemu.
Na koniec przedstawiamy kilka zadań, które można rozwiązać opisaną metodą.